En Juillet 2004, la sonde européenne Cassini-Huygens nous a livré ses premiers clichés des anneaux de Saturne.

Elle a également photographié Titan, le plus gros satellite de Saturne, situé à une distance R_T de Saturne. L’excentricité orbitale des satellites étant très faible, on supposera leurs trajectoires circulaires.

Dans tout l’exercice, on se place dans le référentiel saturno-centrique, centré sur Saturne et dont les trois axes sont dirigés vers trois étoiles lointaines supposées fixes.

On considère que la planète Saturne et ses satellites sont des corps dont la répartition des masses est à symétrie sphérique. Les rayons des orbites des satellites sont supposés grands devant leur taille.

Données : G = 6,67´ 10^–11 S.I. : constante de gravitation universelle.

Concernant Titan : R_T = 1,22´ 10⁶ km (rayon de l’orbite de Titan).

Concernant Saturne : R_S = 6,0´ 10⁴ km (rayon de la planète Saturne).

Ts = 10 h 39 min (période de rotation de Saturne sur elle-même).

M_S = 5,69´ 10²⁶ kg (masse de Saturne).

1. Quelques caractéristiques de Titan :

1.1. Forces : On considère que la seule force gravitationnelle exercée sur Titan provient de Saturne.

1.1.1. Nommer la (les) force(s) extérieure(s) appliquée(s) au satellite Titan, de masse M_T.

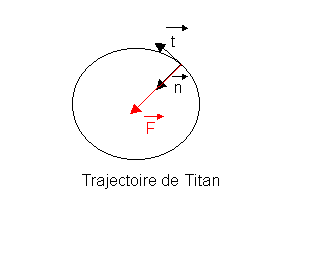
1.1.2. Représenter qualitativement sur un schéma, Saturne, Titan, et la (les) force(s) extérieure(s) appliquée(s) sur Titan.

1.1.3. Donner l’expression vectorielle de cette (ces) force(s).

1.2. Accélération et vitesse

On étudie le mouvement du centre d’inertie T de Titan. S est le centre d’inertie de Saturne.

Soit le vecteur unitaire porté par la droite ST dirigé de S vers T.

1.2.1. Exprimer son accélération vectorielle en précisant la loi utilisée.

1.2.2. On se place dans la base orthonormée (,) centrée en T dans laquelle est un vecteur unitaire porté par la tangente à la trajectoire et orienté dans le sens du mouvement et un vecteur unitaire perpendiculaire à et dirigé vers l’intérieur de la trajectoire ( = –).

On donne l’expression de dans la base orthonormée (,) : = a_t + a_n .

Donner les expressions littérales de a_t et de a_n en fonction de la vitesse v du satellite.

1.2.3. À quelle composante se réduit l’accélération vectorielle de Titan dans la base orthonormée (,) ? Compléter alors le schéma précédent, avec la base orthonormée (,) et l’accélération de Titan.

1.3. Type de mouvement

1.3.1. Montrer que le mouvement de Titan est uniforme.

1.3.2. Retrouver l’expression de la vitesse de Titan sur son orbite autour de Saturne : v =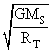

2. D’autres satellites de Saturne :

Après le survol de Titan, la sonde Cassini a survolé le satellite Encelade en février 2005.

On peut considérer que dans le référentiel saturno-centrique, Encelade à un mouvement de révolution circulaire uniforme, dont la période (en jour terrestre), est T_E = 1,37 et le rayon est R_E.

2.1. Loi de Kepler

La relation qui lie la période T de révolution d’un satellite, sa vitesse v et le rayon R de son orbite est T = . Sa vitesse de révolution autour de Saturne est donnée par : v = .

2.1.1. Retrouver la troisième loi de Kepler .

2.1.2. Utiliser la troisième loi de Kepler pour déterminer la valeur du rayon R_E de l’orbite d’Encelade.

3. Sonde saturno-stationnaire :

On cherche dans cette partie à déterminer l’altitude h à laquelle devrait se trouver la sonde Cassini pour être saturno-stationnaire (immobile au-dessus d’un point de l’équateur de Saturne).

3.1. Quelle condition doit-on avoir sur les périodes Ts (rotation de Saturne sur elle-même) et Tc (révolution de Cassini autour de Saturne) pour que la sonde soit « saturno-stationnaire »?

3.2. Altitude de la sonde

3.2.1. En utilisant la troisième loi de Kepler donnée à la question 2.1.1. , montrer que l’altitude h de la sonde peut se calculer avec la relation: h =

3.2.2. Calculer la valeur de h.

1.1 Forces

Titan subit la force d’interaction gravitationnelle exercée par Saturne.

1.1.2

Voir schéma ci-dessous ( est un vecteur unitaire)

1.1.3

1.2 Accélération et vitesse.

1.2.1 D’après la seconde loi de Newton, appliquée à Titan, réduit à son centre d’inertie T, dans le référentiel Saturno-centrique : ( étant la seule force subie par Titan).

Donc : donc

1.2.2

Cette question (base de Frénet) ne fait plus partie des programmes officiels actuels (2007) . Nous pouvons toutefois observer que dans la mesure où la trajectoire de Titan peut être considérée comme circulaire et que la force est centrale (son support passe par le centre de Saturne) , alors (composante tangentielle de ) est nulle .

Pour répondre à la question posée (hors programme) , disons que l'intérêt de la base de Frénet , sachant que dans cette base a_t=dv/dt , avec v , mesure algébrique de la vitesse, est de pouvoir démontrer assez rapidement que si la trajectoire du satellite est circulaire , alors , le mouvement est uniforme .

En effet , a_t=0 , implique que dv/dt est nulle et par conséquent , la primitive v est constante , ce qui signifie que le mouvement est uniforme .

L'expression de a_n (a_n=v²/r) doit par contre être connue pour le baccalauréat en TS .

1.2.3 Le vecteur accélération du centre d'inertie de Titan peut par conséquent s'écrire :

puisque (composante tangentielle nulle) et qu'en raison de la seconde loi de Newton (

1.3.1 La façon la plus simple de démonter que le mouvement est uniforme est celle qui est présentée ci-dessus (a_t=0 entraîne v=constante) .

Si l'on veut rester dans l'esprit du programme nous partons de F=F_n=M_Ta_n (puisque les composantes tangentielles de et sont nulles) :

Cela s'écrit aussi : 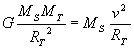et donc finalement

Comme la trajectoire de Titan est circulaire R_T= cte . De plus G et M_S sont aussi des constantes . Par conséquent la vitesse est constante (mouvement uniforme)

1.3.2. Finalement :

2- D’autres satellites de Saturne :

2.1.1 Loi de Kepler

Le mouvement de Titan étant uniforme , nous pouvons écrire v=2pR_T/T et donc :

2.1.2

Soit : R_E = = 2,38 x 10⁸ m

3- Satellite saturno-stationnaire

Un satellite saturno-stationnaire reste à la verticale du même point. Sa période de révolution est égale à la durée d’un jour sur Saturne. T_C = T_S.

3.2 Altitude de la sonde

3.2.1 Nous avons vu à la question 2.1.2 : où R_C est le rayon de l’orbite de la sonde Cassini.

Or R_C = R_S + h et T_C = T_S donc :

h = = 5,2 x 10⁸ m