DEVOIR MAISON 1 PHYSIQUE-CHIMIE (2003/2004) - TS10
I/Oscillations électriques et cuve à ondes :
Pour étudier les ondes progressives à la surface de l'eau on utilise une cuve à ondes. Un vibreur permet de générer des ondes planes circulaires de fréquence N à la surface de l'eau. Les crêtes des vages donnent des rides brillantes et les creux des rides sombres sur un écran. AB= 7 cm dans la cuve .
A- étude du vibreur :
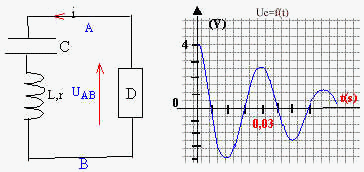
La surface de l'eau est excitée par de l'air pulsé: les pulsations sont crées par une petite pompe. Leur fréquence peut être régle de 10 à 40 Hz gràce à un oscillateur électrique entretenu. Les oscillations électriques peuvent être obtenues gràce à un condensateur de capacité C= 30mF relié à une bobine d'inductance L et de résistance r.
1-A la date t=0 s on relie le condensateur portant la charge Q0 à la bobine. On visualise la tension aux bornes du condensateur.

a/ uC(t) est-elle une tension périodique ? Comment qualifie-t-on un tel
régime oscillatoire ?
b/Calculer l'énergie E0 emmagasinée par le condensateur à t=0 s
c/Calculer l'énergie E1 emmagasinée par le condensateur à t1=30ms.
d/Interpreter la variation d'énergie entre 0 et 30 ms.
e/Ce dispositif peut-il être utilisé pour obtenir des oscillations à la surface de
l'eau ?
2.On désire entretenir les oscillations :
a/Pour ce faire on introduit un montage équivalent à un dipôle D fournissant la
puissance P=ri² où r a la même valeur que la résistance de la bobine. Quel est le
nouveau régime des oscillations ?
b/Quelle est alors la forme de uC(t) ? ce montage peut-il être utilisé pour
générer des ondes sinusoïdales dans la cuve.
c/Quelle est la fréquence propre des oscillations si L= 0,75 h et C=30mF
?
B- Etude des ondes.
1/Mesure de la célérité des ondes :
A l'aide du vibreur, on crée des ondes progressives sinusoïdales de fréquence N à
la surface de l'eau. Le phénomène observé possède une longueur d'onde l.
a-1/Définir la longueur d'onde.
a-2/Quelle relation existe-il entre la longueur d'onde l, la
fréquence N et la célérité v des ondes observées ?
b/A l'aide de la photo 1 déterminer la longueur d'onde l 1
et calculer la célérité des ondes si N1 = 8 Hz.
c/La photo 2 est réalisée avec une fréquence N2 = 17 Hz.
c-1/ Montrer que la célérité des ondes varie avec la fréquence.
c-2/Comment appelle t-on ce phénomène ?
c-3/Décrire une expérience permettant d'observer ce phénomène avec des ondes lumineuses.

2.Influence de la profondeur de l'eau sur la célérité des ondes
a/On place sur le fond de la cuve une plaque P de plexiglas transparent. On génère des ondes incidentes planes sinusoïdales de fréquence N=11 Hz
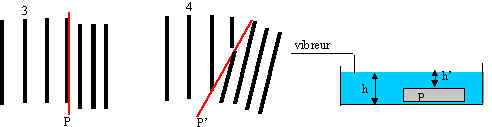
.Montrer en utilisant la photo3 que la célérité des ondes dépend de la profondeur
de l'eau.
b-On remplace la plaque P par une plaque P' et on obtient la photo 4. Quel phénomène
observe-t-on ?
c-1/En eau très profonde, pour les vagues de basse fréquence on peut démontrer que la
célérité v des ondes ne dépend pratiquement plus de h. Elle varie alors
proportionnellement à la période T suivant la loi : v = g /(2p)
*T où g =9,8 m/s²est l'intensité de la pesanteur. Calculer v1 et v2
si N1 = 5 Hz et N2 = 10 Hz ainsi que les longueurs d'ondes l1 et l2
correspondantes.
c-2/On excite sinusoïdalement un point S à partir de l'instant t=0. On observe un point
M situé à 10 m de S. A quel instant t1 le point M entre-t-il en vibration si
la fréquence excitatrice est N1= 5Hz ? Calculer de même l'instant t2
si N2 = 10 Hz.
II/Réactions acido-basiques :
A-Identifier un indicateur coloré :
on dispose d'un flacon d'indicateur coloré avec la seule indication C0= 2,9 10-4 mol/L. La mesure du pH donne 4,18. On en déduit [H3O+]=6,6 10-5 mol/L. Le couple acide base présent dans l'indicateur coloré est noté Hind / Ind-. La solution de l'indicateur coloré a été préparée à partir de la forme acide Hind. L'équation de Hind avec l'eau s'écrit : Hind + H2O = Ind- + H3O+.(1)
1-Soit un volume V= 100 mL de la solution de l'indicateur coloré, déterminer le taux d'avancement final de la réacrion de l'acide Hind avec l'eau. Cet acide est-il totalement dissocié dans l'eau. Justifier.
2-Donner l'expression de la constante d'acidité Ka de la réaction (1).
3-Si Ka = 1,9 10-5 , calculer le pKa du couple Hind / Ind-. et identifier l'indicateur d'après les données suivanbtes :
| indicateur | couleur acide | zone de virage | couleur basique | pKa |
| hélianthine | jaune orangé | 3,1 - 4,4 | rouge | 3,7 |
| vert de bromocrésol | jaune | 3,8 - 5,4 | bleu | 4,7 |
| bleu de bromothymol | jaune | 6 - 7,6 | bleu | 7 |
| phénolphtaléine | incolore | 8,2 - 10 | fuschsia | 9,4 |
B- dosage d'une solution d'acide chlorhydrique concentré :
Sur l'étiquette du flacon on lit 33% minimum en masse d'acide chlorhydrique. On veut connaître la concentration molaire c0 de cette solution notée S0.
* On dilue 1000 fois S0 et on obtient une solution S1 de concentration c1.
* On prélève V1=100 mL de S1 que l'on dose par conductimétrie à l'aide d'une solution de'hydroxyde de sodium de concentration cB= 0,1 mol/L. On donne le graphe (a) représentant la conductance de la solution en fonction de lu volume V de la solution titrante versée
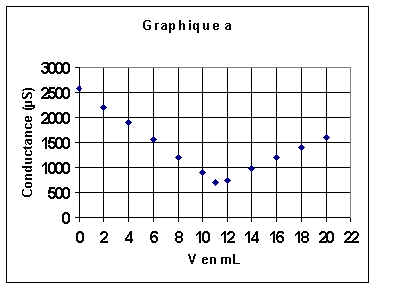
dosage conductimétrique - figure a
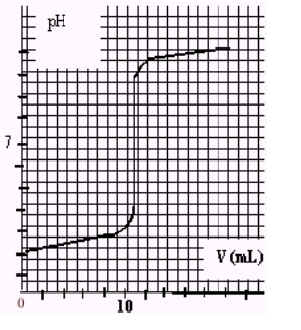
dosage pH-mètrique : figure b
1-Ecrire la réaction du dosage.
2-Déterminer (graphe (a) ) le volume équivalent VE.
3-Donner la relation entre c1, cB, VE et V1 à l'équivalence. Calculer c1.
4-En déduire c0
5-Calculer la masse m0 de chlorure d'hydrogène HCl dissous dans un litre de solution (on rappelle que HCl est un acide qui eéagit totalement avec l'eau (Cl=35,5 ; H= 1 g/mol. )).
6)La solution S0 a une masse volumique de 1160 g.L-1 . Quelle est la masse m d'un litre de solution S0 ?
7)Le pourcentage massique de la solution S0 représente la masse de chlorure d'hydrogène HCl dissous dans 100 g de solution . Calculer le pourcentage massique de la solution S0 .
8)Sur le graphe donnant le dosage suivi par pH-métrie, indiquer la zone de virage de l'indicateur coloré identifié ci-dessus. Décrire le changement de couleur observé lors du dosage.
9)Dans la liste des indicateurs colorés y-at-il un indicateur coloré mieux adapté pour repérer l'équivalence du dosage ? Justifier.
Correction du dm1 - 2004
I/Oscillations électriques et cuve à ondes :A-Etude du vibreur
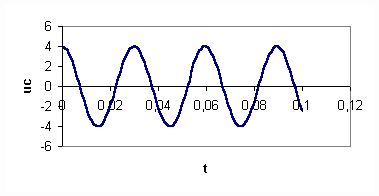
1-a :La tension uc(t) n'est pas périodique . Il s'agit d'un régime pseudo-oscillatoire amorti .
b: E=1/2 Cuc2
à t=0 uc=4 V et E0=2,4 . 10-4 J . C'est l'énergie emmagasinée par le condensateur à t=0.
c: à t1=30 s uC= 2,7 V et donc E1= 10-4 J
d : l'énergie maximale du condensateur diminue au cours du temps : cet amortissement est du aux pertes par effet Joule dans les parties résistives du circuit .
e: Si ce dispositif est utilisé pour produire des oscillations à la surface de l'eau , celles-ci "disparaissent" assez rapidement : le dispositif n'est donc pas adéquat pour obtenir des oscillations qui "durent" à la surface de l'eau .
2/-a: le nouveau régime obtenu en utilisant une résistance "négative" est un régime oscillatoire entretenu .
b: uc(t) est alors une fonction sinusoïdale du temps de la forme uc(t)=Uc,m cos(w0 t+j) .Le montage peut alors être utilisé pour générer des ondes sinusoïdales dans la cuve . Uc,m est l'amplitude de la tension uC et w0 la pulsation .
c:Nous savons que la fréquence propre des oscillations est donnée par la relation :
![]()
B-Etude des ondes
1/mesure de la célérité des ondes :
a-1 :La longueur d'onde l est la distance "parcourue" par l'onde sur une durée égale à une période T.
a-2 : l=V.T = V/N où V est la célérité de l'onde dans le milieu de propagation , et N la fréquence de l'onde .
b:Sur la figure 1 , la distance AB correspond à 2,5 l (pour le principe de la mesure , voir le livre page 39 doc 17) : l1 = AB/2,5 = 7/2,5 = 2,8 cm . Par conséquent V1 = l1*N1 = 22,4 cm.s-1 (attention aux unités).
Avec la figure 2 , nous obtenons : AB=4,5 l2 d'où l2 = 1,55 cm et V2 = 26,4 cm.s-1 .
c-1 Les résultats précédents font apparaître que la célérité des ondes n'est pas la même pour deux fréquences différentes : autrement dit , la célérité dépend de la fréquence .
c-2 : lorsque la célérité des ondes dépend de la fréquence , le milieu est dit dispersif (phénomène de dispersion).
c-3 : Un prisme en verre est un milieu dispersif pour la lumière . Ainsi lorsqu'un prisme en verre est éclairé par un faisceau de lumière blanche , les angles de réfraction dépendent des fréquences des différentes couleurs qui composent la lumière blanche et nous pouvons ainsi observer le spectre de la lumière blanche sur un écran (doc 8 livre page 50)
2/Influence de la profondeur sur la célérité des ondes .
a: Soit l0 la longueur d'onde mesurée sur la photo 3 , avant la plaque P (profondeur h) et l1 la longueur d'onde après la plaque (profondeur h'). La photo fait apparaître que l0= 1,8 l1 . Soient V0 et V1 les célérités respectives de l'onde dans les deux zones :
V0= l0*N et V1 = l1*N et donc finalement V0=1,8 * V1 .Il est donc clair que la célérité des ondes dépend de la profondeur de l'eau .
b:la photo 4 fait apparaître le changement de direction de l'onde lorsqu'elle passe de la première zone (profondeur h - célérité de l'onde V0 ) à la seconde zone (profondeur h' - célérité de l'onde V1 ) .
Ce phénomène est bien connu en optique lorsqu'un rayon lumineux (un rayon est perpendiculaire aux surfaces d'ondes) arrive sur un dioptre (surface séparant deux milieux d'indices n=c/V différents - c est la célérité de la lumière dans le vide et V la même célérité mais dans le milieu considéré ) sous un angle d'incidence différent de 0 °.
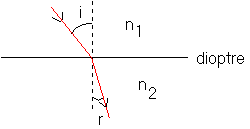
c-1 :
![]()
Application numérique :
v1 = 0,3 m.s-1 v2 = 0,16 m.s-1 . l1 = 6 cm l2=1,6 cm
c-2 : Dt = d/V ; Dt1 = 33 s Dt2= 62 s
II/Réactions acido-basiques :
A/Identification d'un indicateur coloré .
1/
Avancement Hind + H2O = H3O+ + Ind- |
||||||
initial |
X=0 |
2,9 . 10-5 mol |
solvant |
0 |
0 |
|
en cours |
X |
2,9.10-5- X |
X |
X |
||
si totale |
Xmax |
2,9 .10-5 - Xmax=0 |
Xmax |
Xmax |
||
final |
Xf |
2,9 . 10-5 -Xf |
Xf=[H3O+]*V |
Xf |
||
n(Hind introduite) = C0V = 2,9 10-4 * 0,1 = 2,9 10-5 mol .
Xmax = 2,9 10-5 mol (disparition totale du réactif limitant si la réaction est totale)
Le taux d'avancement final est par définition :
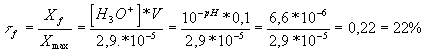
tf < 1 : la réaction de l'indicateur coloré avec l'eau est donc limitée , autrement dit , l'indicateur n'est pas totalement dissocié dans l'eau .
2-
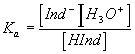 :
:
c'est la constante d'équilibre de la réaction de l'indicateur avec l'eau .
3- pKa = -log Ka = 4,7 : c'est le pKa du vert de bromocrésol .
B/Dosage d'une solution d'acide chlorhydrique concentré .
1/La réaction de dosage est celle d'un acide qui réagit totalement avec l'eau (Hcl) et celle d'une base qui se dissocie totalement dans l'eau (NaOH) : c'est donc la réaction entre les ions H3O+ (apportés par HCl ) et OH- (apportés par NaOH ) :
H3O+ + OH- -------> 2H2O (1)
Les ions Na+ et Cl- sont certes présents dans le milieu réactionnel , mais ce sont des espèces inertes : c'est la raison pour laquelle ils ne figurent pas dans l'équation de la réaction de dosage .
2/Nous sommes à l'équivalence lorsque la conductance est minimale (voir cours de 1S) : sur le graphe (a) , nous lisons : VE= Vb,equiv = 11 mL . On peut remarquer au passage que cette valeur est confirmée par la courbe (b) .
3/A l'équivalence , les réactifs ont été mélangés dans les proportions stoechiométriques de la réaction de dosage (1) .
Cela signifie ici n(H3O+ initial) = n(OH- versés à l'équivalence)
Or ,tenant compte du caractère total des réactions de HCl et de NaOH avec l'eau , nous pouvons écrire : n(H3O+ initial) = n(HCl introduit )= C1V1
n(OH- versés à l'équivalence ) = n(NaOH) = CbVb,equiv
ou finalement C1V1 = CbVE
AN : C1 = 0,011 mol.L-1
4/Comme la solution mère a été diluée 1000 fois , la concentration en acide de la solution mère est C0= 11 mol.L-1 .
5/La masse m0 de chlorure d'hydrogène dissoute dans un litre de solution mère est m0 = n0 * MHCl = C0*1*36,5 = 401 g
6/ m = r*V = 1160 * 1 = 1160 g : c'est la masse d'un litre de solution mère .
7/Pourcentage massique en HCl : 401 / 1160 = 34,5 %
8/La zone de virage du vert de bromocrésol est située dans l'intervalle de pH :3,8 - 5,4 .Au cours du dosage le pH du milieu ractionnel étant tout d'abord de l'ordre de 3 , l'indicateur coloré présente une teinte jaune (couleur de la forme acide de l'indicateur : Hind ) . Le pH augmentant au fur et à mesure que l'on verse de la soude , l'indicateur coloré prend ensuite une teinte bleue (pH > 5,4 - couleur de la forme basique Ind- du couple ) .
9/Les coordonnées du point d'équivalence sont pHE =7 et VE=11 mL . Le bleu de bromothymol est l'indicateur le mieux adapté pour réaliser le dosage , car sa zone de virage contient le point d'équivalence .
Toutefois , dans le cas présent , la variation du pH est suffisamment brutale autour du point d'équivalence (le pH passe rapidement de 4 à 10) , pour que le vert de bromocrésol permette de faire une mesure précise de l'équivalence .