LYCEE FREDERIC CHOPIN – NANCY – BACCALAUREAT BLANC 2007
PHYSIQUE CHIMIE
Durée de l'épreuve 3h30
Les calculatrices sont autorisées
Les élèves des spécialités MATH et SVT traiteront les exercices :1, 2, 3, 5
Les élèves de la spécialité SPC traiteront les exercices :1, 2, 3, 4
Exercice n°1 :Circuits électriques (5 points) [Tous les élèves]
L'équation différentielle ![]() (1), ( a et b étant des grandeurs constantes),
admet 2 solutions :
(1), ( a et b étant des grandeurs constantes),
admet 2 solutions :![]() si b
si b ![]() 0 et x(t) =
0 et x(t) = ![]() si b = 0, avec X0 grandeur constante
si b = 0, avec X0 grandeur constante
PARTIE A:
On réalise expérimentalement le circuit électrique ci-contre. Ce circuit comporte une bobine d'inductance L et de résistance r = 11,8 W (donc non négligeable), et un conducteur ohmique de résistance R = 12 W , alimenté par un générateur délivrant une tension continue E = 6,1 V
L'évolution des grandeurs variables, tension u(t) et intensité i(t), est obtenue par voie informatique.
· La voie EA0 permet de visualiser la tension E
· La voie EAl permet de visualiser la tension UBc
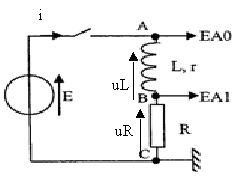
1.Étude expérimentale :
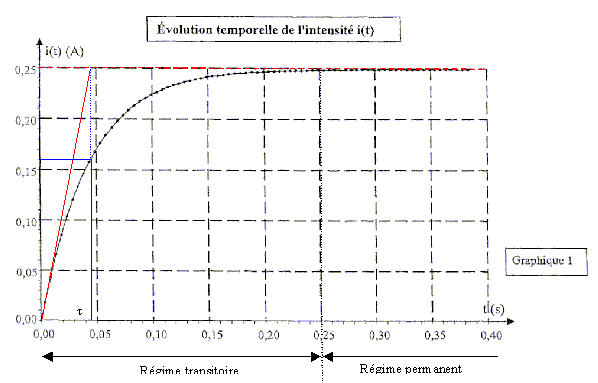
Courbe expérimentale donnant l'évolution de l'intensité i(t) :
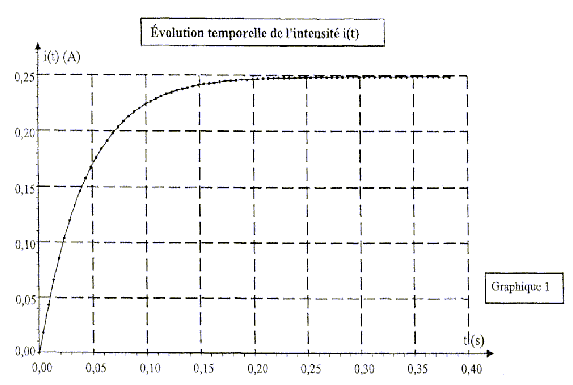
1-1:Évaluer graphiquement la durée du régime transitoire. Aucune justification n'est demandée.
1-2 t étant la constante de temps associée au dipôle {bobine-conducteur ohmique} :
1-2-1:Donner l'expression littérale de t en fonction des paramètres du circuit.
1-2-2:En déduire l'expression de l'inductance de la bobine et calculer sa valeur (elle doit être comprise entre 0,95 H et 1,20 H).
2.Modèle théorique
2-1:En utilisant la loi d'additivité des tensions et en respectant l'orientation du circuit, établir l'équation différentielle vérifiée par l'intensité i(t).
2-2:Par identification avec l'équation (1) vérifier que ![]() et donner l'expression de b .
et donner l'expression de b .
2-3:En déduire l'équation horaire littérale i(t) en fonction de {r, R, L et E}.
2-4:Montrer que cette solution valide bien l'équation établie en 2.1.
3-Confrontation des résultats expérimentaux avec le modèle théorique.
On rappelle que ![]() et
et ![]() = 1
= 1
On appellera I l'intensité en régime permanent (l'intensité étant constante). Donner l'expression littérale de I. Calculer sa valeur. Est-elle en accord avec la valeur expérimentale obtenue ?
PARTIE B :
On associe maintenant la bobine précédente, d’inductance L et de résistance r, à un condensateur de capacité C = 0,3 mF préalablement chargé. A l’aide d’une carte d’acquisition reliée à un ordinateur et d’un logiciel de traitement de données, on obtient le document suivant représentant :
d’une part, les variations de la charge q du condensateur en fonction du temps t :
ordonnée q (axe gradué à gauche)
d’autre part, les variations de l’énergie E bob emmagasinée dans la bobine en fonction du temps t : ordonnée E bob(axe gradué à droite).
On notera E cond l’énergie emmagasinée dans le condensateur
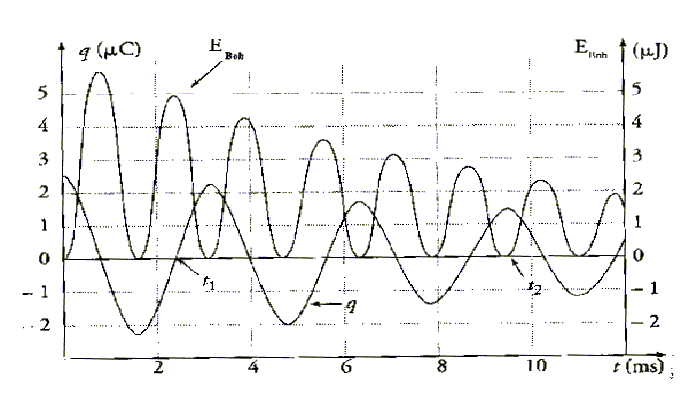
1. Détermination de la valeur de l’inductance L :
1.1. Déterminer graphiquement la valeur de la pseudo-période des oscillations.
1.2. En assimilant la pseudo-période à la période propre des oscillations, déduire la valeur de l’inductance L. Ce résultat est-il en accord avec celui trouvé dans la partie A ?
2. Déduire du graphique, à l’instant t1 = 2,4 ms indiqué sur le document :
2.1. la valeur de l’énergie E1, bob emmagasinée dans la bobine à l’instant t1.
2.2 la valeur de l’énergie E1, cond emmagasinée dans le condensateur à l’instant t1
2.3. la valeur de l’énergie totale E1 du circuit à l’instant t1
3. A l’instant t 2 = 9,5 ms indiqué sur le document, déterminer à partir du graphique :
3.1. La valeur de l’énergie E2, bob emmagasinée dans la bobine à l’instant t2
3.2. La valeur de l’énergie E2, cond emmagasinée dans le condensateur à l’instant t2
3.3. La valeur de l’énergie totale E2 du circuit à l’instant t2.
4. Energie totale du circuit :
4.1 L'énergie totale est-elle ou non conservée ?
4.2 Quel dipôle dans le circuit est responsable de la conservation ou la non conservation de l'énergie ?
4.3 Quel phénomène explique ce résultat ?
Exercice n°2 : Radioactivité – Du chlore dans l'eau (5 points) [Tous les élèves]
Du chlore dans les eaux souterraines
Il existe deux principaux isotopes stables du chlore (dont les nombres de masse sont 35 et 37) trouvés dans les proportions respectives de 3 pour 1 et qui donnent aux atomes en vrac une masse molaire atomique apparente de 35,5 g.mol - 1. Le chlore a 9 isotopes avec des nombres de masse s’étendant de 32 à
40. Seulement trois de ces isotopes existent à l’état naturel : le Le «chlore 36» D’après un article d’encyclopédie |
Données :
- Relation entre le temps de demi-vie t1/2 et la constante radioactive ? : t1/2 = ![]()
- Relation entre l’activité A d’un échantillon et le nombre moyen de noyau N présent dans cet échantillon, à une date t donnée : A(t) = ?. N(t)
- 1 an = 3,156 *10 7 s
- Célérité de la lumière dans le vide : c =3*10 8 m.s - 1
- Masse molaire atomique du chlore : M(Cl) = 35,5 g.mol - 1
- Constante d’Avogadro : NA = 6,02 * 10 23 mol - 1
-1 u = 931,5 MeV/c2
- Masse et numéro atomique (ou nombre de charge) de quelques particules et noyaux :
Particule ou noyau |
proton |
neutron |
chlore 36 |
argon 36 |
Masse (u) |
1,007 26 |
1,008 65 |
35,958 43 |
************ |
Z |
1 |
0 |
17 |
18 |
1. Dans l’article, l’auteur indique des valeurs 35 et 37 pour les isotopes stables du chlore.
Que désignent plus précisément ces valeurs pour un noyau de chlore ?
2. Définir le terme « isotopes ».
3. Donner le symbole complet du noyau de « chlore 36 » et sa composition.
4. Calculer, en MeV, l’énergie de liaison d’un noyau de « chlore 36 ». Exprimer le résultat final avec quatre chiffres significatifs.
On rappelle que 1 eV = 1,602 * 10 – 19 J.
5. Le texte évoque la réaction de désintégration d’un noyau de « chlore 36 ».
Écrire l’équation de cette réaction, en indiquant :
- les lois utilisées ;
- le type de radioactivité mise en jeu.
6. Donner la définition du temps de « demi-vie » t1/2 du « chlore 36 ».
7. Constante radioactive
Calculer la constante radioactive de l’isotope de « chlore 36 » .
8. Une bouteille contient un volume V= 1,5 L d’eau minérale. Sa teneur en ions chlorure est indiquée sur l’étiquette et vaut cm = 13,5 mg.L - 1.
8.1. Calculer la quantité d’ions chlorure, en mol, dans l’eau de cette bouteille.
8.2. On suppose que le rapport du nombre de noyaux de « chlore 36 » au nombre total de noyaux de chlore présents dans cette eau minérale est celui donné dans l’article.
Montrer que le nombre N de noyaux de « chlore 36 » présents dans cette bouteille est N = 2,4 * 10 8 .
8.3. En déduire la valeur de l’activité en « chlore 36 » de l’eau que contient cette bouteille.
8.4. En déduire la valeur du nombre de désintégrations de noyaux de « chlore 36 » par jour.
9. Datation d’une eau souterraine
L’étude des isotopes radioactifs apporte des informations concernant la durée du transit souterrain d’une eau c'est-à-dire l’âge de la nappe phréatique. Les ions chlorures Cl - (aq) sont presque toujours présents dans les eaux minérales naturelles et ne sont que rarement impliqués dans les interactions eaux - rochers. Dans les eaux de surface, le « chlore 36 » est renouvelé et la teneur en « chlore 36 » peut être supposée constante, ce qui n’est pas le cas dans les eaux souterraines des nappes phréatiques. Le « chlore 36 », de demi vie 3,01*10 5 ans, est donc un traceur particulièrement adapté à l’étude des eaux souterraines anciennes.
Pour dater des eaux plus récentes, on peut utiliser le « carbone 14 », de demi-vie 5,73 *10 3 ans, présent dans les ions carbonates CO32-(aq) dissous par exemple.
9.1. Loi de décroissance radioactive.
On considère un échantillon, de volume V donné, d’eau issue d’une nappe phréatique. On note :
- N0 le nombre moyen de noyaux de « chlore 36 » présents dans cet échantillon à l’instant de date t0 = 0 s de la constitution de la nappe.
- N(t) le nombre moyen de noyaux de « chlore 36 » dans l’eau extraite aujourd’hui de cette nappe et donc non renouvelée en « chlore 36 ».
Écrire la loi de décroissance radioactive liant N(t), N0 et t1/2.
9.2. Datation d’une eau souterraine.
On admet que N0 est égal au nombre moyen de noyaux de « chlore 36 » présents dans un échantillon de même volume V d’eau de surface.
Déduire de la loi de décroissance écrite précédemment l’âge d’une nappe phréatique dont l’eau non renouvelée ne contient plus que 38 % du nombre de noyaux de « chlore 36 » trouvée dans les eaux de surface.
Exercice n°3 : Constante d'équilibre (6 points) [Tous les élèves]
Détermination d'une constante d'équilibre par deux méthodes
L'acide éthanoïque CH3CO2H, également appelé
acide acétique, réagit de façon limitée avec l'eau
selon l'équation chimique : CH3CO2H (aq) + H2O
(l) = CH3CO2–(aq) + H3O+(aq)
1. ÉTUDE PH-METRIQUE
Une solution d'acide éthanoïque, de concentration molaire initiale c1
= 2,7.10 –3 mol.L–1 et de volume
V1 = 100 mL a un pH de 3,70 à 25°C.
1.1 Déterminer la quantité de matière initiale d'acide éthanoïque n1.
1.2. Faites un tableau d'avancement en fonction de n1, x max ou xf. Exprimer puis calculer l'avancement maximal théorique noté x max . Justifier la réponse.
1.3. Déduire, de la mesure du pH, la concentration molaire finale en ions oxonium de la solution d'acide éthanoïque. Exprimer puis calculer l'avancement final expérimental de la réaction noté xf
1.4. Donner l'expression littérale du taux d'avancement final t 1 de la réaction. Vérifier, en posant l'opération, que t 1 est égal à 7,4.10 –2. La transformation étudiée est-elle totale ? Justifier la réponse.
1.5.1. Exprimer puis calculer la concentration molaire finale en ions éthanoate CH3CO2–(aq).
1.5.2. Exprimer la concentration molaire finale effective de l'acide éthanoïque [CH3CO2H]f. Calculer sa valeur.
1.6.1.Exprimer la constante d'équilibre K1 associée à l'équation de cet équilibre chimique
1.6.2.Vérifier, en posant l'opération, que la valeur de la constante d'équilibre K1 associée à l'équation de cet équilibre chimique est égale à 1,6.10 –5.
2. ÉTUDE CONDUCTIMÉTRIQUE
On mesure ensuite, à 25°C, la conductivité d'une solution d'acide
éthanoïque de concentration
c2 = 1,0.10–1 mol.L–1. Le conductimètre
indique : s = 5,00.10–2 S.m–1.
On rappelle l'équation de la réaction entre l'acide éthanoïque et l'eau :
CH3CO2H (aq) + H2O (l) = CH3CO2– (aq) + H3O+ (aq)
2.1. On néglige toute autre réaction chimique. Citer les espèces ioniques majoritaires présentes dans cette solution. Donner la relation liant leur concentration molaire.
2.2.Donner l'expression littérale de la conductivité s de la solution en fonction des concentrations molaires finales en ions oxonium et en ions éthanoate.
2.3.Donner l'expression littérale permettant d'obtenir les
concentrations molaires finales ioniques en fonction de s , l ![]() , l
, l ![]() .
.
2.4.Déterminer la valeur de la concentration molaire finale en ions oxonium et éthanoate en mol.m-3, puis en mol.L–1 .
Données: l ![]() =
35,9.10 –3 S.m².mol–1 l
=
35,9.10 –3 S.m².mol–1 l ![]() = 4,1.10 –3 S.m².mol–1
= 4,1.10 –3 S.m².mol–1
2.5.L'expérimentateur affirme que dans le cas présent, la dissociation de l'acide éthanoïque est suffisamment limitée pour pouvoir faire l’approximation suivante:
la concentration molaire finale en acide éthanoïque est
quasiment égale à la concentration molaire initiale en acide éthanoïque: [CH3CO2H]f
![]() c2
c2
Vérifier,en posant l'opération, que la valeur de la constante d'équilibre K2 associée à l'équation de cet équilibre chimique est égale à 1,56.10 –5.
3. CONCLUSION: COMPARAISON DES RÉSULTATS OBTENUS
On vient d'étudier deux solutions d'acide éthanoïque de concentrations initiales différentes.
Les résultats sont rassemblés dans le tableau ci-dessous.
Concentration molaire initiale d'acide éthanoïque |
Constante d'équilibre |
Taux d'avancement final |
|
Étude pH-métrique |
c1 = 2,7.10 –3 mol.L–1 |
K1 = 1,6.10 –5 |
t 1 = 7,40.10 –2 |
Étude conductimétrique |
c2 = 1,0.10 –1 mol.L–1 |
K2 |
t 2 = 1,25.10 –2 |
3.1.La constante d'équilibre K dépend-elle de la concentration initiale en acide éthanoïque? Justifier la réponse à partir du tableau.
3.2. Le taux d'avancement final d'une transformation chimique limitée
dépend-il de l'état initial du
système chimique? Justifier la réponse à partir du tableau.
3.3.Un élève propose les deux affirmations suivantes. Préciser si
elles sont justes ou fausses, une
justification est attendue.
Affirmation 1: Plus l'acide est dissocié et plus le taux d'avancement final t est grand.
Affirmation 2: Plus la solution d'acide éthanoïque est diluée, moins l'acide est dissocié.
Exercice 4 : Hydrodistillation de l'estragon : (4 points) [Elèves de la spécialité SPC]
L'estragole et l'anéthole (appelé camphre d'anis) sont des substances utilisées en parfumerie et entrant dans la composition d'arômes pour les aliments et les boissons. L'estragole existe dans les essences d'estragon (70 à 75%), de basilic (70 à 75%), d'anis et de fenouil ; l'anéthole existe dans les essences d'anis et de fenouil. L'essence d'estragon est obtenue par hydrodistillation des feuilles d'estragon.
Il faut 120 kg de feuilles d'estragon pour obtenir 1 kg d'huile essentielle .
A/ Hydrodistillation des feuilles d'estragon :
Données:
estragole |
dichlorométhane |
eau |
eau salée |
|
densité |
0,96 |
1,34 |
1 |
1,1 |
solubilité de l'estragole |
très soluble |
peu soluble |
très peu soluble |
Température de fusion de l'estragole : Tf = -6,8 °C
Température d'ébullition de l'estragole : TE = 112 °C
-Mode opératoire
*Dans un ballon de 500 mL, on introduit 200 mL d'eau distillée, des feuilles finement découpées d'estragon frais et quelques grains de pierre ponce (ou des billes de verre).
*On réalise le montage d'hydrodistillation représenté ci-après et on porte à ébullition le mélange contenu dans le ballon.
*On laisse se poursuivre la distillation jusqu'à obtenir environ 50 mL de distillat dont l'aspect est trouble *On ajoute au distillat 5 g de chlorure de sodium que l'on dissout par agitation.
*On verse ensuite le distillat dans une ampoule à décanter et on introduit 10 mL de dichlorométhane.*Après agitation et décantation, on récupère la phase organique.
*On ajoute ensuite du sulfate de magnésium anhydre ; après filtration on obtient une solution H ("huile essentielle").
Questions
1-Quel est le rôle de l'eau introduite dans le ballon ?
2-Dans le schéma du montage d'hydrodistillation, nommer les différentes parties numérotées de 1 à 5 et préciser la fonction des tubulures latérales du dispositif 4.
3-Expliquer l'aspect trouble du distillat
4-Justifier l'ajout du chlorure de sodium au distillat en utilisant les données.
5-a : Faire le schéma de l'ampoule à décanter, après agitation et
décantation. Préciser les positions de la phase aqueuse et de la phase organique.
Justifier à partir des données.
5-b:Quelle précaution liée à la sécurité doit-on prendre lors de l'agitation de
l'ampoule à décanter ?
5-c:Pourquoi après décantation récupère-t-on la phase organique plutôt que la phase aqueuse ?
6-Quel est le rôle du sulfate de magnésium anhydre ?
7-A 20°C, l'estragole est-il gazeux, liquide ou solide ? Justifier
8-On a utilisé 500 g de feuilles d'estragon . Quelle masse maximale d'huile essentielle pouvait-on espérer obtenir ?
B/ Chromatographie sur couche mince (CCM)
On se propose de vérifier la présence d'estragole dans l'essence d'estragon obtenue par hydrodistillation, ainsi que dans des essences d'estragon, de basilic et d'anis vert du commerce. On souhaite vérifier simultanément la présence d'anéthole dans l'essence d'anis.
Mode opératoire
On réalise les six solutions suivantes dans le cyclohexane :
- une d'estragole pur : E - une d'essence d'estragon du commerce : C
- une d'anéthole pur : A - une d'essence de basilic du commerce : B
- une de la solution H - une d'essence d'anis du commerce : V.
Sur une plaque de silice sensible au rayonnement ultra-violet, on effectue les dépôts de chacune de ces six solutions. L'éluant est un mélange de cyclohexane à 97,5% d'acétate d'éthyle à 2,5% en volume. La plaque est révélée avec une lampe émettant des radiations ultraviolettes. Le chromatogramme est reproduit ci-après :
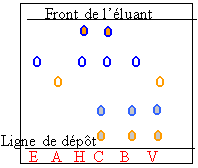
Le chromatogramme permet-il toutes les vérifications attendues ? Justifier.
Exercice 5 : Cinétique chimique : (4 points) [Elèves des spécialités MATH et SVT]
Pour étudier la cinétique d'une réaction produisant des gaz, on peut suivre l'évolution de la pression des gaz produits en fonction du temps .L'expérience suivante a pour but de déterminer le temps t1/2 de demi-réaction de la réaction entre le magnésium métallique et l'acide chlorhydrique dont l'équation est :
Mg(s) + 2H3O+aq = Mg2+aq + H2(g) + 2H2Oliq
La transformation sera supposée totale .
Protocole expérimental
Dans un ballon on introduit un volume Vliq=10,0 mL d'une solution concentrée d'acide chlorhydrique (H3O+ + Cl-) de concentration C=8 mol.L-1 .
A l'instant initial , on plonge un ruban de magnésium de longueur L=5,1 cm.
Très rapidement , on ferme ce ballon avec un bouchon percé qui permet de relier, par un tuyau, le contenu du ballon avec un manomètre .On note régulièrement la valeur de la pression indiquée sur le manomètre .
Données :
*Masse linéique (ou masse par unité de longueur) du ruban de magnésium : l=1,0 g.m-1 .
*Masse molaire du magnésium : M(Mg)= 24,3 g.mol-1 .
*Volume du ballon vide : V0=100 mL (on néglige le volume du connecteur devant celui du ballon).
*Pression atmosphérique au moment de l'expérience: patm=1,1.105 Pa
*Température au moment de l'expérience : T=293 K
*Constante des gaz parfaite : R=8,31 SI.
A/Etude théorique de la réaction :
1/Déterminer les quantités de matière de chacun des réactifs à l'état initial.
2/D'après l'équation de la réaction, déterminer la valeur Xmax de l'avancement maximal .
3/A l'instant initial , la pression dans le ballon est égale à la pression atmosphérique patm. En effet, le ballon ne contient en plus de la solution acide, que de l'air. Puis au fur et à mesure de la production de gaz, la pression va augmenter .
Son expression générale dans le cadre de l'expérience est : p = patm + p(H2) où p(H2) est la pression du dihydrogène occupant tout le volume disponible dans le ballon.
3-1 :Donner l'expression de la quantité de matière de dihydrogène H2 produite, à l’instant t, en fonction de l'avancement X.
3-2 : En déduire l'expression de l'avancement X en fonction de la pression totale p des volumes V0 et Vliq, de la température T et de patm .
On considèrera que le dihydrogène H2 se comporte comme un gaz parfait , c'est à dire que :
![]() où n(H2) est la quantité de H2
formée , T la température exprimée en K, R la constante des gaz parfaits et V le volume
(en m3) occupé par le gaz dans le ballon , soit ici V=V0 -Vliq
où n(H2) est la quantité de H2
formée , T la température exprimée en K, R la constante des gaz parfaits et V le volume
(en m3) occupé par le gaz dans le ballon , soit ici V=V0 -Vliq
B/Suivi de la pression :
L'évolution de l'avancement de la réaction en fonction du temps est représentée sur le graphe ci-après :
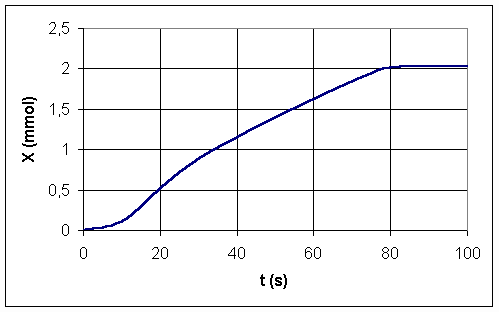
1/Définir le temps de demi-réaction t1/2
2/Déterminer graphiquement , la valeur de t1/2 .
3/ D'après les questions A-2 et A-3-1 déterminer la valeur de la pression maximale pmax attendue.
4/Au bout de 80 s, peut-on dire que la réaction est terminée ? Justifier .
5/Définir la vitesse de la réaction . Comment évolue cette vitesse au cours du temps ? Justifiez clairement votre réponse .
C/Influence de certains paramètres :
1/Si on avait utilisé la même masse de magnésium que précédemment, mais sous forme de limaille (poudre fine), la valeur du temps de demi-réaction aurait-elle été plus grande ou plus petite que dans l'expérience précédente ? Justifier brièvement .
2/Même question si on avait placé le ballon dans un cristallisoir d'eau chaude .
Correction
I/Circuits électriques
PARTIE A
1-Étude expérimentale
1-1:L'établissement du courant dans la bobine n'est pas instantané. Durant le régime transitoire, l'intensité du courant i(t) augmente jusqu'à une valeur constante I = 0,25 A. Graphiquement on peut estimer la durée du régime transitoire à D t = 0,25 s.
1-2-1:L'expression littérale de la constante de temps t en fonction des paramètres du circuit est:
![]()
1-2-2 :Détermination de l'inductance L :
La relation précédente donne: L = t .(R + r). Connaissant R = 12 W et r = 11,8 W , il faut évaluer t pour déterminer L.
Nous pouvons utiliser la méthode de la tangente pour déterminer t: la tangente à i(t) à l'instant t=0 coupe l'asymptote i=0,25 A à t=t . Graphiquement , nous trouvons t=0,045 s = 45 ms
Finalement: L = 45.10-3 ´ (12 + 11,8) = 1,1 H L = 1,1 H
2-1:Modèle théorique
2-1:La loi d'additivité des tensions donne: E = uR + uL.
Compte tenu de la définition de l'intensité algébrique i (définie sur le schéma): uL
= r.i + L.![]()
uR = R.i et donc: E = r.i + L.![]() + R.i . Finalement:
+ R.i . Finalement: ![]() +
+ ![]()
2-2:Par identification avec l'équation (1): ![]() , pour laquelle x Û i, il vient:
, pour laquelle x Û i, il vient: ![]() et b
=
et b
= ![]()
2-3:L'équation horaire i(t) s'obtient par identification avec la solution: ![]()
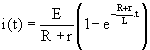
2.4 Cette solution valide l'équation établie en 2.1 si ![]() +
+ ![]() est égal à
est égal à ![]() :
:
On a: ![]() =
= ![]() =
= ![]()
Et: ![]() =
= ![]()
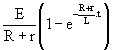 =
= 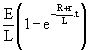
Soit ![]() +
+ ![]() =
= ![]() +
+ 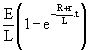
Finalement : ![]() +
+ ![]() =
= ![]() donc la solution
i(t) valide bien l'équation établie en 2.1.
donc la solution
i(t) valide bien l'équation établie en 2.1.
3 :Confrontation des résultats expérimentaux avec le modèle théorique.
L'intensité I en régime permanent est obtenue pour tà ![]() .
.
Or ![]() lorsque tà
lorsque tà ![]() donc: i(tà
donc: i(tà ![]() ) = I =
) = I = ![]()
Application numérique: I = ![]() = 2,6.10-1 A.
= 2,6.10-1 A.
La valeur lue sur le graphique est 2,5.10-1 A . Les deux valeurs sont voisines (écart relatif de 4 %).
PARTIE B :
1 – Valeur de l'inductance
1-1 La pseudo-période des oscillations se détermine à partir de la courbe q(t) : on peut par exemple dététerminer la durée entre deux maxima successifs : T=3 ms
1-2 :![]() est équivalent à :
est équivalent à :![]()
AN : ![]() , résultat de l'ordre de grandeur de celui
trouvé dans A
, résultat de l'ordre de grandeur de celui
trouvé dans A
Energie :
2-1 :Nous lisons sur le graphique à t1 : E1,bob= 5 µJ
2-2 : E1,cond= q2(t1)/(2C) = 0 J (puisque q(t1)= 0 C
2-3 : E1=E1,bob+E1,cond= 5 µJ = 5.10-6 J
3-1 : E2,bob= 0 J
3-2 : E2,cond= q2(t2)/(2C)=(1,5.10-6)2/(2*0,3.10-6)=3,75.10-6 J
3-3 :E2=E2,cond+E2,bob= 3,5 µJ
4-1 : il est clair que l'énergie totale n'est pas conservée (E2 < E1)
4-2: C'est la partie résistive du circuit (résistance totale RT=R+r) qui est responsable de la non conservation de l'énergie .
4-3 : C'est l'effet Joule (transformation d'énergie électrique en énergie thermique) qui est responsable de la non conservation de l'énergie totale du circuit .
Exercice 2 : Radioactivité -Du chlore dans les eaux souterraines
1. 35 et 37 représentent les nombres de masses. C'est à dire le nombre de nucléons (protons +neutrons) présents dans ces noyaux isotopes.
2. Des noyaux isotopes possèdent le même nombre de protons mais un nombre de neutrons différent.
3. Le noyau ![]() contient 17 protons et 36 – 17 =
19 neutrons.
contient 17 protons et 36 – 17 =
19 neutrons.
4. EL1 = D m.c² où D m représente le défaut de masse du noyau ![]()
D m = (Z´ mP + (A–Z)´ mn ) – mX où mP = masse d'un proton, mn masse d'un neutron et mX masse du noyau de chlore 36.
EL1 = [(Z´ mP + (A–Z)´ mn ) – mX]. c²
EL1 = [17´ 1,00726 + 19´ 1,00865 – 35,95843] u.c2=[17´ 1,00726 + 19´ 1,00865 – 35,95843]*931,5*MeV/c2*c2 = 306,7 MeV
5. Au cours d'une transformation nucléaire, il y a conservation du nombre de charges et du nombre de nucléons.
On obtient ![]() à
à ![]() +
+ ![]() +
+![]()
Un électron est libéré au cours de cette désintégration, il s'agit de radioactivité de type b –.
6. Soit N0 le nombre de noyaux de chlore 36 , initialement présents dans un échantillon.
Au bout d'une durée (demi-vie)de t1/2 = 301´ 103 ans , N0/2 noyaux se seront désintégrés. L'échantillon contiendra encore N0/2 noyaux de chlore 36.
7. D'après les données: t1/2 = ![]() , donc l =
, donc l = ![]() ; l =
; l = ![]() =
= ![]() =7,3.10-14
s-1
=7,3.10-14
s-1
8.1. n = ![]() et cm =
et cm = ![]() soit m = cm´ V
soit m = cm´ V
donc n = ![]() =
= ![]() = 5,7´ 10–4 mol d'ions chlorure
dans l'eau d'un bouteille de 1,5 L
= 5,7´ 10–4 mol d'ions chlorure
dans l'eau d'un bouteille de 1,5 L
8.2. Soit NT le nombre total de noyaux de chlore dans la bouteille.
NT = n ´ NA
"Le rapport du nombre de noyaux de Cl-36 au nombre total de noyaux de Cl présents dans l’environnement est de 7,0×10 –13 actuellement."
soit ![]() et donc N = 7,0´ 10–13 ´ NT
= = 2,4.108 noyaux c.q.f.d.
et donc N = 7,0´ 10–13 ´ NT
= = 2,4.108 noyaux c.q.f.d.
8.3. A(t) = l . N(t) = ![]() .N(t) ; A(t) =
.N(t) ; A(t) = ![]() ´ 2,4´
108 =1,75 . 10-5 Bq
´ 2,4´
108 =1,75 . 10-5 Bq
Ceci représente le nombre moyen de désintégrations de noyaux de chlore par seconde.
8.4. Soit D le nombre de
désintégrations de noyaux de « chlore 36 » par jour:D = A(t)´ 24 ´ 3600
D = 1,5 Ce nombre peut ne pas être entier puisqu'il s'agit d'une moyenne.
9. Datation d’une eau souterraine
9.1. N(t) = N0 ´ e–l .t = N(t) = N0´ ![]()
9.2. N(t) = ![]() N0
donc
N0
donc ![]() = 0,38 =
= 0,38 =![]() =
= ![]()
–![]() .t = ln
.t = ln ![]() = ln 0,38 et finalement : t = –(ln 0,38).
= ln 0,38 et finalement : t = –(ln 0,38).![]() = 4,2´ 105 ans
= 4,2´ 105 ans
Exercice 3 : Constante d'équilibre
1.ÉTUDE pH-MÉTRIQUE
1.1. quantité de matière initiale d'acide éthanoïque : n1 = c1´ V1 ; n1 = 2,7.10–3 ´ 0,100 =2,7.10-4 mol .
1.2. |
Avancement |
CH3CO2H(aq) + H2O(l) = CH3CO2–(aq) + H3O+(aq) |
|||
État initial |
x = 0 |
n1 |
en excès |
0 |
0 |
État final théorique |
x = xmax |
n1 – xmax |
en excès |
xmax |
xmax |
État final expérimental ou état d'équilibre |
x = xf |
n1 – xf |
en excès |
xf |
xf |
Si la transformation est totale, l’acide éthanoïque est totalement consommé, soit n1 – xmax = 0
xmax = n1 soit xmax = 2,7´ 10–4 mol
1.3. [H3O+(aq)]f = 10–pH [H3O+(aq)]f = 10–3,70 = 2,0.10–4 mol.L–1
[H3O+(aq)]f = ![]() soit xf = [H3O+(aq)]f
´ V1 = 2,0.10–4 ´
0,100 = 2,0.10–5 mol
soit xf = [H3O+(aq)]f
´ V1 = 2,0.10–4 ´
0,100 = 2,0.10–5 mol
1.4. t 1 = ![]() =
=
![]() = 0,74´ 10–5´ 104 = 7,4.10–2 ; la
transformation est limitée car t 1 < 1.
= 0,74´ 10–5´ 104 = 7,4.10–2 ; la
transformation est limitée car t 1 < 1.
1.5.1. D’après l’équation chimique [H3O+(aq)]f
= [CH3CO2–(aq)]f = ![]() = 2,0.10– 4 mol.L–1
= 2,0.10– 4 mol.L–1
1.5.2. c1 = [CH3CO2H(aq)]ini = [CH3CO2H(aq)]f + [CH3CO2–(aq)]f
[CH3CO2H(aq)]f = c1 – [CH3CO2–(aq)]f = 2,7.10–3 – 2,0.10– 4 = 2,5.10–3 mol.L–1
1.6.1 : K1 = 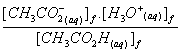
1.6.2 :K1 = ![]() =
= ![]() = 1,6.10–5
= 1,6.10–5
2. ÉTUDE CONDUCTIMÉTRIQUE
2.1. Présence d’ions éthanoate CH3CO2– , d’ions oxonium H3O+, on néglige la présence des ions hydroxyde car le pH est très acide (=3,70). D’après l’équation chimique [H3O+(aq)]f = [CH3CO2–(aq)]f
2.2. s = ![]() .[CH3CO2–(aq)]f
+
.[CH3CO2–(aq)]f
+ ![]() .[H3O+(aq)]f
.[H3O+(aq)]f
2.3 s = (![]() +
+![]() ).[H3O+(aq)]f
).[H3O+(aq)]f
[H3O+(aq)]f = [CH3CO2–(aq)]f
= ![]()
2.4 [H3O+(aq)]f = [CH3CO2–(aq)]f
= ![]() =
= ![]() =
= ![]() mol.m-3
mol.m-3
[H3O+(aq)]f = [CH3CO2–(aq)]f =1,25 mol.m–3 = 1,25.10–3 mol.L–1
2.5. K2 = 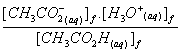 =
=![]() (en tenant compte de l'approximation proposée c2
pratiquement égal à [CH3CO2H]f)
(en tenant compte de l'approximation proposée c2
pratiquement égal à [CH3CO2H]f)
K2 = ![]() =
= ![]() =
1,56.10–5
=
1,56.10–5
3. CONCLUSION : COMPARAISON DES RESULTATS OBTENUS
3.1. La constante d’équilibre K ne dépend pas de la concentration
initiale en acide éthanoïque, puisque avec deux concentrations c1 ![]() c2différentes on obtient la même valeur de K (K1=K2).
c2différentes on obtient la même valeur de K (K1=K2).
3.2. Oui, le taux d’avancement final d’une transformation
chimique limitée dépend de l’état initial du système. En effet avec deux
concentrations initiales différentes (c1 ![]() c2),
on obtient deux taux d’avancement différents (t1
c2),
on obtient deux taux d’avancement différents (t1
![]() t2)
t2)
3.3. Affirmation 1 : Plus l’acide est dissocié et plus le taux d’avancement final t est grand.
Affirmation juste : t = ![]() , plus l’acide est dissocié , plus xf est
grand et alors t est plus grand. (xmax étant
constant).
, plus l’acide est dissocié , plus xf est
grand et alors t est plus grand. (xmax étant
constant).
Affirmation 2 : Plus la solution d’acide éthanoïque est diluée, moins l’acide est dissocié.
Affirmation fausse : c1 < c2 donc la solution 1 est davantage diluée.
On a obtenu t 1 > t 2 , dans la solution 1 l’acide s’est davantage dissocié.
Rq : Pour apprécier la validité de cette affirmation , on exploite en fait , l'affirmation précédente.
Exercice 5 : Cinétique chimique
A/Etude théorique
1/ * Magnésium : nMg = m/M = (l*L)/M= 5,1.10-2/24,3 = 2,1.10-3 mol (attention aux unités)
*ions oxonium : nH3O+= C*Vliq = 80.10-3 mol
2/nMg/1 < nH3O+/2 : le magnésium est donc le réactif limitant . Lorsque la réaction est totale (ce qui est le cas ici) , à la fin de la réaction , le réctif limitant est totalement consommé .
Donc nMg – Xmax = 0 d'où Xmax = 2,1.10-3 mol .
3-1 : D'après l'équation de la réaction : nH2 = X (nH2 : quantité de dihydrogène produit par la réaction)
3-2 :En reprenant la loi des gaz parfaits dont l'expression est donnée dans l'énonce , nous obtenons :
![]()
B/Suivi de la pression
1/Temps de demi-réaction t1/2: c'est la durée pour laquelle X=Xmax /2 (la réaction est à "moitié" terminée)
2/ C'est à dire ici X = 1 mol. Sur le graphique , nous lisons : t1/2= 33 s
3/A partir de l'expression étéblie dans A/ , nous obtenons :
![]()
4/Au delà de t=80 s , X ne varie plus : cela signifie que la réaction est terminée (X=Xmax)
5/![]() : c'est la définition de la vitesse de
réaction (Vsol est le volume de la solution). Autrement dit , la vitesse de
réaction , le volume de la solution Vsol étant constant , est proportionnelle
à la dérivée de l'avancement de la réaction par rapport au temps . Or dX/dt est égal
au coefficient directeur de la tangente à X(t) à l'instant considéré .
: c'est la définition de la vitesse de
réaction (Vsol est le volume de la solution). Autrement dit , la vitesse de
réaction , le volume de la solution Vsol étant constant , est proportionnelle
à la dérivée de l'avancement de la réaction par rapport au temps . Or dX/dt est égal
au coefficient directeur de la tangente à X(t) à l'instant considéré .
A partir de la courbe X(t) , nous pouvons donc dire :
*Entre 0 et 10 s la vitesse de la réaction est relativement faible (coefficient directeur de la tangente voisin de 0)
*Puis la viresse augmente à environ t=10 s , reste pratiquement constante en diminuant toutefois légèrement entre 20 et 80 s.
*A t=80 s la vitesse de réaction devient nulle (réaction terminée)
C/Influence de certains paramètres
1/Si le magnésium avait été sous forme de limaille , la vitesse de la réaction aurait été plus élevée : en effet cela aurait favorisé les contacts entre les réactifs et les chocs auraient été plus efficaces (donc réaction plus rapide)
2/La température est un facteur cinétique et nous savons que plus la température est élevée , plus la vitesse de la réaction est élevée .
Exercice 4 : hydrodistillation de l'estragon :
A/Hydrodistillation
1/Hydrodistillation est synonyme "d'entraînement à la vapeur" . Autrement dit , au cours de l'hydrodistillation , l'eau est transformée en vapeur (100 °C sous la pression atmosphérique normale) et la vapeur d'eau entraîne avec elle l'essence d'estragon .
2/1 : ballon ; 2:chauffe-ballon ; 3:thermomètre ; 4:condenseur à courant d'eau ascendant ; 5:erlenmeyer
3/Le distillat est notamment constitué d'eau et d'estragole : ces deux composants ne sont pas miscibles (estragole peu soluble dans l'eau ). C'est la raison pour laquelle le distillat présente un léger trouble .
4/L'estragole , déjà peu soluble dans l'eau , l'est encore moins dans l'eau salée (c'est ce qu'indique le tableau). Cela favorisera le passage de l'estragole vers la phase organique au cours de la décantation .
5/-a :
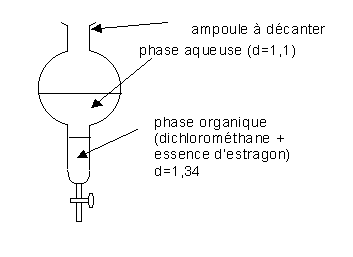
La phase inférieure est la phase organique car celle-ci a une densité plus élevée que celle de la phase aqueuse.
b:lors de l'agitation de l'ampoule à décanter , il est important de dégazer . Cette opération consiste à ouvrir le robinet avec une main , tout en inclinant l'ampoule et en maintenant le bouchon avec l'autre main .
Il va de soi qu'il ne faut absolument pas diriger l'ouverture de l'ampoule vers qui que ce soit !
c:On récupère la phase organique car c'est elle qui contient l'essence d'estragole (l'estragole est très soluble dans le dichlorométhane et elle ne l'est pratiquement pas dans l'eau salée)
6/Le sulfate de magnésium anhydre permet d'éliminer les quelques traces d'eau qui pourraient encore "accompagrer" l'essence d'estragole .
7/A 20°C , l'estragole est liquide . En effet Tf < 20 < TE
8/L'énoncé précise qu'il faut 120 kg de feuilles d'estragon pour obtenir 1 kg d'huile essentielle :Avec 500 g=0,5 kg , nous pouvons donc espérer obtenir 1/120*0,5 =4,1.10-3 kg = 4,1 g d'essence .
B/Chromatographie
Principe : la tache correspondant à un corps pur est au même "niveau" sur le chromatogramme , que celui-ci soit isolé ou mélangé (mélange) à d'autres corps purs .
Le chromatogramme permet de vérifier :
* la présence d'estragole (E) dans l'essence d'estragon(H) obtenue par hydrodistillation
* la présence d'estragole (E) dans l'essence d'estragon du commerce (C)
* la présence d'estragole (E) dans l'essence de basilic (B)
*L'essence d'anis contient de l'anéthole
Par contre , il n'y a pas d'estragole (E) dans l'anis vert du commerce .