Lycée Frédéric CHOPIN- NANCY
BACCALAUREAT BLANC -PHYSIQUE-CHIMIE (12/02/05)
_______________________________________________________________________________
Durée de l'épreuve : 3h30
Les calculatrices sont autorisées
Les élèves de la spécialité physique-chimie traitent les exercices I , II , III et IV
Les élèves des spécialités SVT et mathématiques traitent les exercices I , II , III et V
________________________________________________________________________________________
EXERCICE I :ACIDE BENZOIQUE (5 points)
Une solution S d'acide benzoïque C6H5COOH, de concentration massique t = 1,22 g / L, a un pH égal à 3,1.
1/Couple acide-base
1-a :Rappeler la définition d'un couple acide-base.
1-b :Quelle est la base conjuguée de l'acide benzoïque ?
2/Concentration molaire volumique de la solution
On donne les masses molaires atomiques suivantes :
C : 12 g / mol ; O : 16 g / mol ;H : 1 g / mol
Calculer la concentration molaire volumique de la solution étudiée.
3/Taux d'avancement de la réaction
3-a :Ecrire l'équation de la réaction associée à la mise en solution aqueuse de l'acide benzoïque.
Utiliser un tableau d'avancement pour :
3-b:Calculer l'avancement maximal qui serait obtenu si la réaction était totale (on raisonnera sur la préparation de V = 200 mL de la solution S).
3-c:Calculer l'avancement final réellement observé.
3-d :Calculer le taux d'avancement final de la réaction.
4/Influence de la dilution
A partir de la solution S, on prépare V ' = 200 mL d'une solution S' d'acide benzoïque de concentration
C ' = 1,0 . 10-3 mol / L.
Le pH prend la valeur 3,6.
4-a:Comment fait-on pour préparer la solution S' ?
4-b:Calculer le nouveau taux d'avancement final de la réaction entre l'acide et l'eau.
4-c :Commenter le résultat par rapport à celui obtenu avec la solution S.
5/Espèce prédominante .
La constante d'acidité du couple C6H5COOH/C6H5COO- est égale à Ka = 6,3.10-5 à 25°C
5-a: Donnez la définition de la constante d'acidité du couple acide benzoïque/ion benzoate
5-b: Calculer le pKa du couple .
5-c:Quelle relation lie le pH et le pKa pour le couple étudié ?
5-d:De la forme acide et de la forme basique du couple considéré , quelle est celle qui prédomine dans la solution S' (pH=3,6) ? Justifiez votre réponse .
6/Déplacement de l'équilibre :
A 200 mL de la solution S , on ajoute sans variation notable de volume 1.10-4 mol d'ions C6H5COO-
6-a : En exploitant l'état final du tableau d'avancement de la question 3-c , calculer le quotient de réaction initial de la réaction 3-a consécutivement à l'ajout des ions C6H5COO-.
6-b : En déduire le sens d'évolution de la réaction 3-a dans la solution S suite à l'ajout d'ions C6H5COO-
EXERCICE II : Elimination de l'alcool par l'organisme (3 points)
Lorsqu'une personne boit de l'alcool, son estomac le laisse passer sélectivement dans le sang , où des enzymes permettent son oxydation .
Données : Masses molaires des atomes en g.mol-1 :
H : 1 ; C : 12 ; O : 16
L'alcool contenu dans les boissons alccolisées est l'éthanol C2H5OH
1/Un automobiliste boit 250 mL d'un liquide contenant 1 mol d'alcool. On suppose que l'estomac ne contient que ce volume de liquide et on suppose ce volume constant pendant le temps considéré ici .
Les données regroupées ci-dessous représentent l'évolution de la concentration en alcool dans son estomac, CE au cours du temps :
| t (min) | 0 | 1,75 | 2,8 | 5,5 | 12 | 18 | 22 |
| CE (mol/L) | 4 | 3 | 2,5 | 1,6 | 0,75 | 0,2 | 0,1 |
Tracer sur la feuille de papier millimétré de l'annexe la courbe Ce=f(t)
2/Dans le cas de ce problème l'alcool ne disparaît pas de l'estomac parce qu'il est transformé chimiquement, mais parce qu'il passe dans le sang . Il est toutefois possible , par analogie avec une réaction chimique , de définir le temps de demi-réaction .
a)Dans le cas présent , donner une définition du temps de demi-disparition t1/2 . Déterminer sa valeur numérique .
b)Dans le cas d'une réaction chimique , si on appelle x l'avancement de la réaction , définir la vitesse de la réaction .
c)Ici , nous nous intéressons à la vitesse de disparition de l'alcool dans l'estomac
: elle peut être définie par ![]() . Donner une
interprétation géométrique de Vd à partir de la courbe tracée
précédemment .
. Donner une
interprétation géométrique de Vd à partir de la courbe tracée
précédemment .
d)Calculer en mol.L-1.min-1 Vd à l'instant t=0 .
3/Le sang et les autres liquides contenus dans le corps seront considérés comme un ensemble unique dénommé <<sang>>, de volume V=40 L .
a)Justifiez le fait qu'à t=22 mn le nombre de mole d'alcool dans le sang soit égal à 0,975 mol .
b) En déduire la concentration molaire puis massique en alcool dans le sang à t=22 mn .
c)La législation fixe un seuil légal à 0,5 g/L pour les automobilistes .La personne est-elle autorisée à conduire à t=22 mn ?
4/Au bout d'une demi-heure , tout l'alcool est passé dans le sang .On considère que la vitesse de disparition de l'alcool dans le sang est alors constante et vaut :
V = 7.10-5 mol.L-1 .min-1 .
Combien de temps après avoir absorbé la boisson alcoolisée l'automobiliste devra t-il attendre avant de pouvoir prendre le volant ?
Note : 3 verres de Pastis apportent environ une mole d'alcool !
EXERCICE III : DEUX CONDENSATEURS FONT LA COURSE (7 points)
A/Etude théorique du dipôle RC
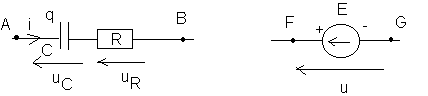
Ci-dessus sont représentés un dipôle RC (R est la résistance du conducteur ohmique et C la capacité du condensateur) et un générateur idéal de tension de force électromotrice E .Les tensions algébriques uC et uR, l’intensité algébrique i et la charge q de l’une des armatures du condensateur sont définies sur les schémas. Ces grandeurs sont des fonctions du temps (t).
1- Donner les relations liant :
1-a- uR et i
1-b- uC et q
1-c- i et q
2- En utilisant les réponses aux trois questions précédentes, déterminer la relation entre uR et uC.
3- On associe les dipôles en série en reliant F à A et G à B.
3-a- Faire le schéma du circuit électrique
3-b- Etablir l’équation différentielle du circuit relative à la tension uC.
3-c- La fonction uC = E ( 1 – e k.t ) est solution de cette équation. Déterminer l’expression de la constante k. (On rappelle que
3-d- Utiliser une analyse dimensionnelle pour déterminer l’unité de la constante k.
B/Course à la charge :
On réalise les deux circuits schématisés ci-dessous . Le commutateur K permet une action simultanée sur chacun des deux circuits .
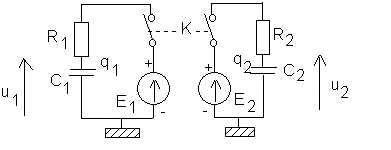
C1 = 1 mF
R1= R2
E1=E2=5 V
A l’instant t = 0, on ferme le double interrupteur K
Sur l’annexe fig 1 est représentée u1(t) (portion de courbe repérée par le chiffre "1") dans l'intervalle de temps [0, 2 s] , tension aux bornes du condensateur C1.
1-Représentez sur votre copie le circuit de charge du condensateur de la branche 1 (R1, C1 , E1 ) . Indiquez sur ce schéma le sens du courant de charge I1 et justifiez le signe de la charge q1
2-a- Montrer qu’à la date t =
t1, constante de temps de la branche 1, la tension aux bornes du condensateur est égale à 63 % de la valeur maximale E de la tension.2-b- En déduire la valeur de
t1.3- Calculer la valeur de la résistance R1. C’est aussi celle de R2.
4-En utilisant la portion de courbe adéquate de l'annexe , à préciser , déterminer la constante de temps
t2 de la branche 2.5-En déduire la capacité C2 du condensateur de la branche 2 .
6-Si on laissait la charge des condensateurs se poursuivre quel serait le condensateur qui serait le le premier chargé ? Justifiez votre réponse .
7-On admet qu'un condensateur est complètement chargé au bout d'une durée de charge supérieure à 5
t . Quelles seraient les durées de charge de chacun des condensateurs ?C/Course à la décharge
A la date t = 2s, on amène les générateurs à 0V, chacun d'entre eux est alors équivalent à un fil .
Parmi les quatres portions de courbes repérées par les chiffres "1" , "2", "3" et "4" sur la fig1 de l'annexe , lesquelles correspondent à la décharge de chacun des deux condensateurs ? Affecter une portion de courbe à chaque condensateur .
Quelles sont les valeurs des constantes de temps de décharge pour chacune des deux branches ?
Déterminer graphiquement la date à laquelle les tensions u1 et u2 sont égales.
4 Quel condensateur sera le premier déchargé ?
D/Connexion des circuits :
Après la décharge précédente des condensateurs , on charge à nouveau les condensateurs C1 et C2 avec cette fois des générateurs de forces électromotrices E1=5 V et E2 = 10 V .
1 : Calculer les charges q1 et q2 (voir schéma) de chacun des condensateurs lorsque ceux-ci sont totalement chargés .
2: Calculer les énergies En1 et En2 emmagasinées alors par chacun des deux condensateurs.
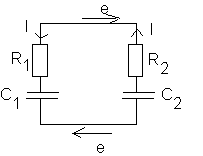
Les condensateurs étant chargés , on réalise un circuit dont le schéma simplifié est représenté ci-dessous . L'interrupteur K1 est ouvert :

Le circuit étant réalisé on ferme l'interrupteur K1 . On constate alors que u2 diminue , alors que u1 augmente
3 :Indiquez sur un schéma à faire sur votre copie le sens du courant dans les résistances R1 et R2
Lorsqu'il n'y a plus de courant dans le circuit , les tensions aux bornes de chacun des condensateurs sont toutes deux égales à
4 :Calculer les nouvelles charges q'1 et q'2 de chacun des condensateurs
5 :Calculer les nouvelles énergies E'n1 et E'n2 de chacun des deux condensateurs .
6 : Comparez En1+En2 à E'n1+E'n2 . L'énergie est-elle conservée au cours du processus ? Commentez
EXERCICE IV :
PHYSIQUE ET VIOLON (5 points) - Elèves de la spécialité physique-chimie uniquementLes questions 4 et 5 de l’exercice sont indépendantes des autres questions.
Chaque réponse devra être clairement rédigée.
Les indications nécessaires à la résolution de l’exercice sont données dans l’énoncé. Aucune connaissance en musique n’est nécessaire pour le résoudre.
En sortant de cours, un élève de classe terminale, violoniste amateur depuis quelques années, examine son
instrument de musique pour en comprendre le fonctionnement.
Le violon possède quatre cordes, que l’on frotte avec un archet.
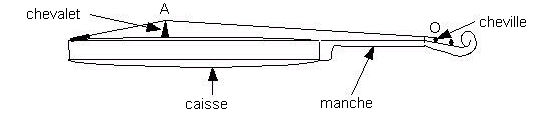
La nature et la tension des cordes sont telles qu’en vibrant sur toute leur longueur (AO = L = 55,0 cm), elles
émettent des notes dont les caractéristiques sont données ci-dessous :
numéro de la corde |
1 |
2 |
3 |
4 |
note |
sol2 |
ré3 |
la3 |
mi4 |
fréquence du son fondamental (en Hz) |
f1=196 |
f2=294 |
f3= 440 |
f4 |
Données :
Une onde progressive se propage le long d’une corde tendue entre deux points fixes à la célérité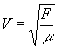 avec
avec
F la tension de la corde et µ sa masse linéique (masse par unité de longueur). Les unités sont celles du système international .
Chaque corde du violon a une masse linéique et une tension qui lui sont propres.
On admet qu’un diapason émet un son de fréquence unique 440 Hz.
1/L’élève fait vibrer une corde tendue de son violon en la pinçant. Il observe un fuseau.
1.1.Celui-ci est-il dû à l'existence d'ondes longitudinales ou transversales ? Justifiez en définissant le terme choisi .
1.2. À partir des connaissances du cours, montrer que la longueur L de la corde vibrante est liée à la longueur
d’onde l par la relation :
![]()
1.3. Les vibrations de la corde sont transmises à la caisse en bois du violon. Quel est le rôle de cette caisse ?
2/ L'élève accorde son violon. Pour chaque corde successivement, il règle la tension de celle-ci afin qu'elle
émette un son correspondant à une fréquence donnée dans le tableau ci-avant . Pour cela , il tourne une cheville.Il s'intéresse d'abord à la corde <<la3>> et règle la hauteur du son en utilisant un diapason (440 Hz) .
Masse linéique de la corde <<la3>> : m=0,95 g.m-1 .
Calculer la tension de la corde après cette opération
3/ Pour jouer une note « la3 » sur la corde « ré3 », l’élève appuie en un point B de celle-ci.
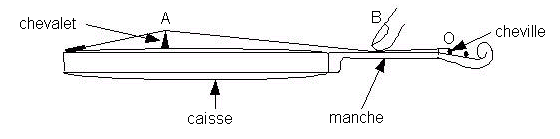
3.1. En admettant que cette opération ne change pas la tension de la corde « ré 3 », quelle grandeur le
violoniste modifie-t-il ?
3.2. À quelle distance du chevalet l’élève appuie-t-il sur la corde pour que la note émise ait pour fréquence fondamentale 440 Hz ?
4/En classe, le son émis par la corde « la3 » du violon d'une part et le son émis par un diapason 440 Hz sont captés par un microphone relié à l’ordinateur. Un logiciel permet d’établir les spectres des fréquences reproduits ci-dessous :
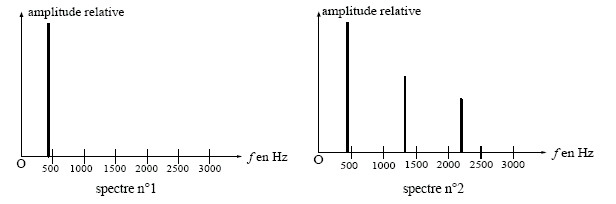
4.1. Identifier chacun des spectres en justifiant la réponse.
4.2. Pour le spectre correspondant au violon, entre les fréquences 0 Hz et 3000 Hz, quelles sont les fréquences
des harmoniques manquants ?
5. À l’aide d’un sonomètre, l’élève mesure un niveau sonore valant 70 dBA lorsqu’il joue une note pendant
quelques secondes en frottant la corde avec l’archet.
Un autre violoniste joue en même temps que l’élève la même note au même niveau sonore.
On suppose que le sonomètre est placé à la même distance des violons.
* Le niveau sonore, en décibel acoustique (dBA) est défini par : ![]() ( log désigne ici le logarithme décimal )
où I est l’intensité sonore et I0
=10-12 W/m2 l’intensité sonore de référence (seuil d’audibilité)
( log désigne ici le logarithme décimal )
où I est l’intensité sonore et I0
=10-12 W/m2 l’intensité sonore de référence (seuil d’audibilité)
* On rappelle que les intensités sonores s’additionnent.
*On rappelle également une propriété de la fonction logarithme : log(a*b)=log a + log b et log an = n*log a
Quel niveau sonore indiquera le même sonomètre lorsque l’élève et le violoniste joueront ensemble ?
6.
Les fréquences fondamentales des quatre cordes du violon ne sont pas choisies au hasard.Trouver la relation mathématique simple entre les valeurs des fréquences données dans le tableau et en déduire la valeur de la fréquence f4 .
EXERCICE 5 :
Echographie (5 points) -Elèves des spécialités SVT et mathématiques uniquementC'est vers 1950 que le docteur Donald montra que l'on pouvait examiner un foetus en faisant passer des impulsions ultrasonores au travers de la paroi abdominale de la mère .
Les ondes sont produites par une sonde jouant le rôle d'émetteur et de récepteur .Les fréquences utilisées dépendent des organes ou tissus biologiques à examiner .Elles s'étendent de 2 à 15 MHz. Par exemple , l'examen du coeur s'effectue avec une fréquence de 3 MHz .
Les ondes ultrasonores se propagent dans les tissus et se réfléchissent , en partie , chaque fois qu'elles changent de milieu .
La sonde posée en un point de la peau reçoit les échos réfléchis par les différentes interfaces tissulaires .Connaissant le temps de retour de l'écho, son amplitude et sa vitesse de propagation, on en déduit des informations sur la nature et l'épaisseur des milieux traversés .Cela est réalisé à l'aide d'un ordinateur qui compile toutes les informations et fournit une image de synthèse des organes sondés .
L'échographie est un examen indolore, simple , non dangereux . Elle permet d'affiner et de compléter les diagnostics dans de nombreux domaines de la médecine . Elle est utilisée aussi en complément des rayons X .
1/Compréhension du texte :
a-Le principe de l'échographie est-il basé sur la transmission , la réflexion , la diffraction ou la dispersion des ondes ultrasonores ? Justifiez à partir du texte .
b-Un examen échographique utilise t-il toujours la même fréquence ? Pourquoi ?
c-1:Donner la nature des ondes ultrasonores .
c-2:Comparer ces ondes aux ondes sonores .
2/Modélisation d'une échographie
On modélise un examen échographique par l'expérience suivante qui permet de déterminer la position "d" d'un organe .
L'expérience est réalisée dans l'air .
L'émetteur E émet des salves d'ondes ultrasonores.La base de temps de l'oscilloscope est réglée sur 1 ms/div .
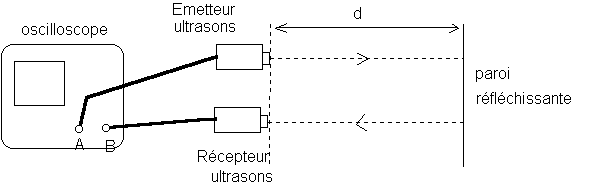
On admettra que les directions de l'onde incidente et l'onde réfléchie sont toutes deux perpendiculaires à la paroi réfléchissante .
a-Interpréter l'oscillogramme obtenu ci-dessous . L'oscillogramme du bas correspond à l'onde réfléchie .
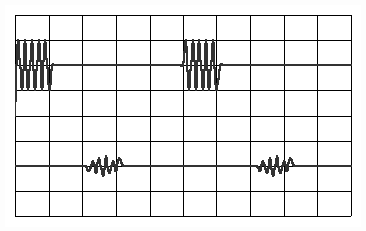
b-Calculer la durée Dt entre l'émission et la réception de l'onde .
c-La célérité des ondes est donnée par ![]() avec g=1,4 , R=8,32 S.I. , T température absolue exprimée en
Kelvin (K = °C + 273 ) et M masse molaire de l'air . Toutes les unités des grandeurs
sont celles du S.I.
avec g=1,4 , R=8,32 S.I. , T température absolue exprimée en
Kelvin (K = °C + 273 ) et M masse molaire de l'air . Toutes les unités des grandeurs
sont celles du S.I.
Une mole d'air a une masse de 29 g . La température de la salle de l'expérience est égale à 17°C.
Calculer la célérité des ondes ultrasonores .
d-En déduire la distance d entre l'émetteur et la paroi réfléchissante .
e-Comparer ce dispositif expérimental avec celui utilisé en échographie:
*Que modélise la paroi réfléchissante ?
*Où se trouverait la peau du patient ?
*la <<sonde >> est-elle la même ?
3/Mesure de la longueur d'onde
Afin de mesurer la longueur d'onde et la célérité des ondes ultrasonores, on réalise l'expérience schématisée ci-dessous , où E est l'émetteur ultrasonore et R1 et R2 des récepteurs ultrasonores .
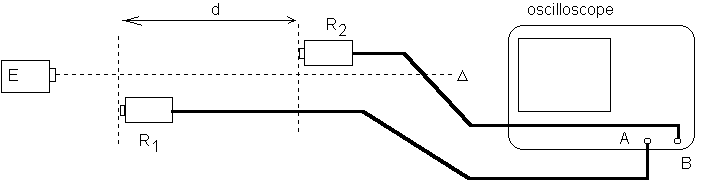
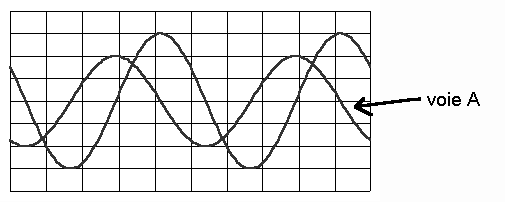
a-1:Comment expliquer le décalage entre les deux courbes ? .
a-2 :Que peut-on dire du coefficient d'amplification verticale sur chacune des deux voies A et B ? Justifiez votre réponse .
b-La base de temps de l'oscilloscope est réglée à 5 µs/div . Calculer la fréquence des ondes ultrasonores .
c-On éloigne R2 de R1 suivant la droite D
c-1:Décrire ce que l'on observe sur l'oscilloscope
c-2:Quelle périodicité de l'onde est mise en évidence ?
c-3:Les signaux captés sont 10 fois en phase sur une distance de 8,5 cm . Calculer la longueur d'onde ainsi que la célérité des ondes ultrasonores .
c-4 :La valeur trouvée est-elle en coïncidence avec celle calculée précedemment ?

ANNEXE
-DOCUMENT A REMETTRE AVEC LA COPIENOM :................................................................ Prénom : ............................................... Classe
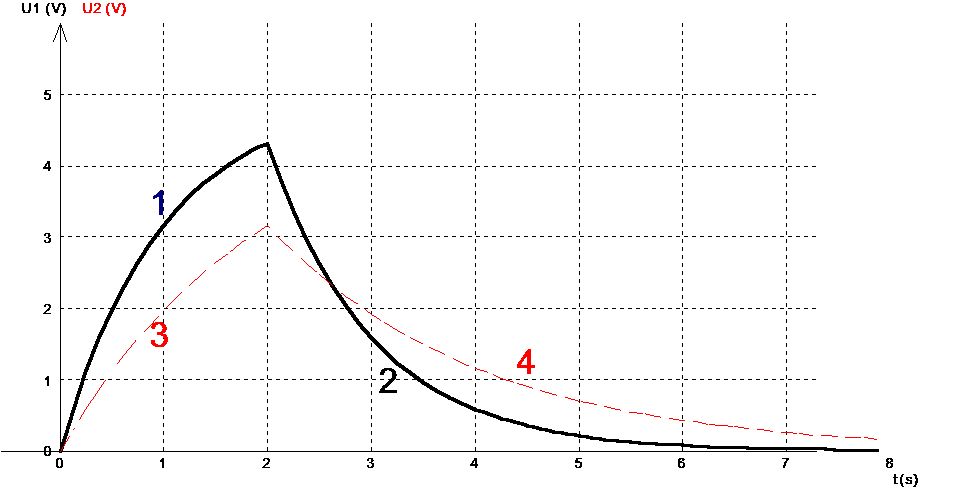
figure 1
BACCALAUREAT BLANC 2005 : Correction
EXERCICE 1 : acide benzoïque :
1/-a : Un acide est un donneur de proton alors qu'une base et un accepteur de proton . Ainsi AH/A- est un couple acide/base : AH=A- + H+ . AH est l'acide et A- sa base conjuguée .
b:La base conjuguée de l'acide benzoïque et l'ion benzoate C6H5COO- .
2/C= t/M : C est la concentration volumique molaire , t le titre massique et M la masse molaire .
MC6H5COOH = 6*12+5+12+32+1= 122 g.mol-1
d'où la concentration volumique molaire de la solution étudiée : C=1,22/122 = 10-2 mol.L-1
3/-a :C6H5COOH + H2O = C6H5COO- + H3O+
b: n0 = CV = 0,01*0,2 = 2.10-3 mol
C6H5COOH + H2O = C6H5COO- + H3O+
| E.I. | 2.10-3 | solvant (excès) | 0 | (0) |
| E.F | 2.10-3 - Xf | excès | Xf | Xf |
L'avancement maximal est égal à l'avancement de la réaction lorsque le réactif limitant(ici l'acide benzoïque) a complètement disparu , c'est à dire lorsque 2.10-3-Xmax = 0 d'ou Xmax = 2.10-3 mol .
c:D'après le tableau d'avancement Xf = [H3O+] * V = 10-pH * V = 10-3,1 *0,2 =1,58.10-4 mol
d: d'où tf = 0,079 = 7,9 %
4/-a:La solution mère a une concentration C0 = 10-2 mol.L-1 et nous voulons préparer V1= 200 mL d'une solution fille de concentration C1=1.10-3 mol.L-1 .
La dilution ne change pas la quantité de soluté introduite : Pour préparer 200 mL de la solution fille il faut donc prélever un volume V0 de la solution mère tel que :
C0V0 = C1V1
V0 = (1.10-3*200/1.10-2) = 20 mL
Pratiquement , on prélève 20 mL de la solution mère avec une pipette jaugée de 20 mL qu'on verse dans une filoe jaugée de 200 mL . On complète progressivement jusqu'au trait de jauge de la fiole jaugée avec de l'eau distillée en agitant entre deux ajouts .Puis on agite à nouveau de façon à bien homogénéiser la solution .
b:Un raisonnement analogue à celui ce la question 3/ donne :
Xf = 10-3,6 * 0,2 = 5.10-5 mol
Xmax = 2.10-4 mol
et donc tf = 0,25 = 25 %
c:Il est clair que le taux d'avancement a augmenté avec la dilution .
5/-a :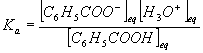
b:pKa = - log(Ka) = 4,2
c:La définition du Ka conduit à :
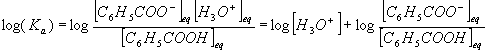
et finalement 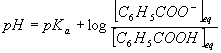
d:Nous sommes dans la situation où pH<pKa et donc 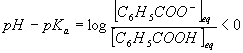
Cette inégalité implique que 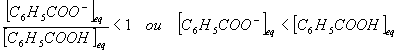
et donc , la forme acide du couple prédomine sur la forme basique .
6/-a: 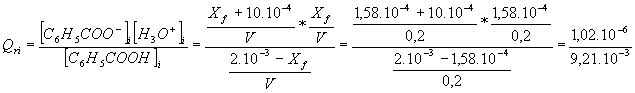
![]()
b: Qr,i > Ka : la raction va donc évoluer spontanément dans le sens indirect c'est à dire de droite à gauche pour la réaction écrite en 3/a .
Exercice 2 : Elimination de l'alcool .
1/ Ce=f(t)
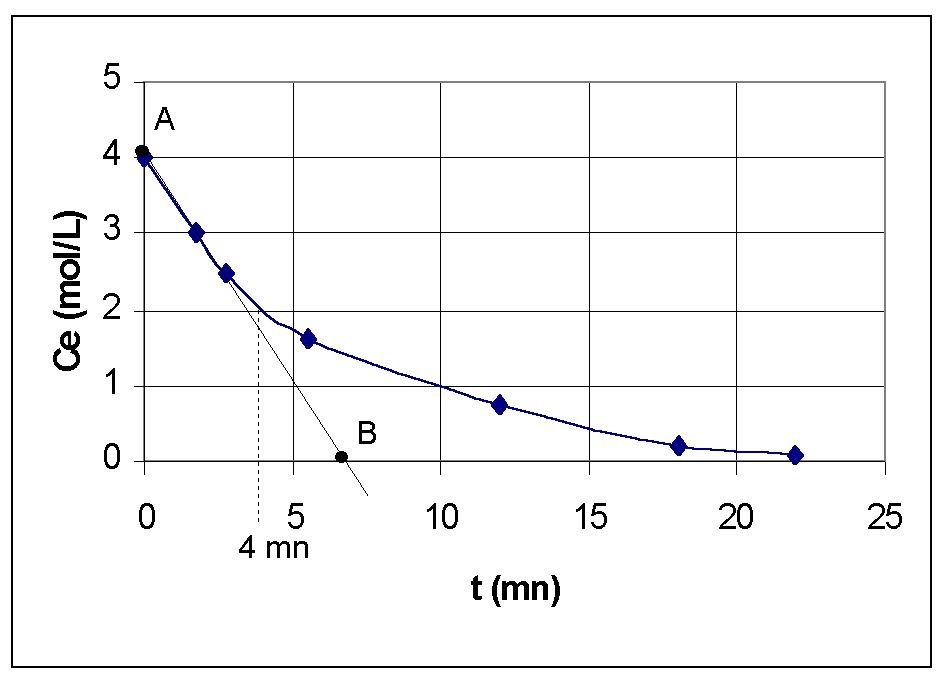
2/-a: Le temps de demi-réaction peut être considéré ici comme l'instant t tel que CE = CE,initial /2 = 2 mol.L-1 .Par lecture graphique , on trouve t1/2 = 4 mn .
b:![]() : c'est la définition d'une vitesse de réaction . Vsolution
est le volume de la solution .
: c'est la définition d'une vitesse de réaction . Vsolution
est le volume de la solution .
c: Vd , la vitesse de disparition de l'alcool est égale à l'opposé du coefficient directeur de la tangente à CE=f(t) à l'instant t considéré .
d: Soient A (tA= 0 min; CE,A= 4 mol/L) et B (tB= 7 mn ;CE,B= 0 mol/L) deux points de la tangente à CE=f(t) à l'instant t=0 .
Le coefficient directeur de la tangente est a= (CE,B - CE,A)/(tB-tA)= - 4/7 = - 0,6 mol.L-1min-1.
D'où : Vd = 0,6 mol.L-1.min-1 .
3/-a:A l'instant t=22 mn il reste dans l'estomac n = CE*V = 0,1* 0,25 = 0,025 mol d'alcool . Le reste 1-0,025 =0,975 est passé dans le sang .
b:la concentration volumique molaire en alcool dans le sang à t=22 mn est donc égale à :
C= 0,975/40 = 2,4.10-2 mol.L-1
Le taux massique correspondant est t= C*M où M est la masse molaire de l'éthanol :46 g.mol-1 .
t= 1,1 g.L-1 .
c: t>0,5 g.L-1 : la personne n'est donc pas autorisée à conduire à t=22 mn .
4/![]() : définition de la vitesse moyenne de dispatition de
l'alcool dans le sang .
: définition de la vitesse moyenne de dispatition de
l'alcool dans le sang .
Si la taux massique de l'alcool dans le sang est égal à 0,5 g/L , cela signifie que la quantité d'alcool est égale à n'= 0,5*VS /M=0,44 mol .
En ayant au départ 1 mole : Dn = 0,44 -1= - 0,56 mol et donc :
![]()
Autrement dit , la personne doit attendre 3h20+30 mn = 3h50 mn après avoir absorbé la boisson alcoolisée pour pouvoir prendre le volant .
Exercice 3 : Condensateurs
A/Etude théorique :
1/-a : uR=Ri b: uC=q/C c: i=dq/dt
2/ ![]()
3/-a :
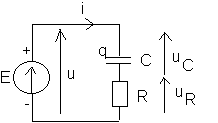
b:![]() : c'est l'équation diférentielle
cherchée .
: c'est l'équation diférentielle
cherchée .
c:A partir de la relation proposée dans l'énoncé , nous obtenons :
![]()
En reportant dans l'équation différentielle , nous obtenons :
![]() ou finalement
ou finalement ![]()
E et ekt étant généralement différents de 0 , l'égalité précédente signifie que la solution proposée pour l'équation différentielle n'est solution qu'à condition que quel que soit l'instant considéré :
1+kRC=0 et donc k = -1/RC= - 1/t en ayant posé t=RC (constante de temps)
d:La dimension de k est l'inverse de celle de RC .
[R] = W = V/A car (loi d'Ohm) : R=u/I
[C]= C/V car C=q/u
C = A*s car dq = i*dt
Finalement :[RC] = V/A *C/V =C/A = s et donc k s'exprime en s-1 .
B/Course à la charge :
1/
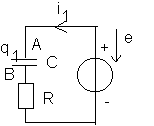
Pendant la charge , le courant est imposé par le générateur et il va donc , à l'extérieur du générateur , du pôle positif vers le pôle négatif comme indiqué sur le schéma (i1) . Cela signifie que dans les conducteurs , les électrons circulent dans l'autre sens : ainsi , l'armature A va perdre des charges négatives (elle va donc se charger positivement) qui vont être transférées via le générateur (pompe à électrons) à l'armature B .
Or q1 est ici la charge de l'armature A : q1 est donc positive .
2/-a :A la date t=t1 : ![]() . Or 1-e-1 = 0,63 . Et donc à t=t1 , nous avons bien uc(t1) = 0,63E
. Or 1-e-1 = 0,63 . Et donc à t=t1 , nous avons bien uc(t1) = 0,63E
b: Comme E = 5 V , nous obtenons uc(t1) = 3,15 V .
En exploitant le graphique de l'annexe , partie 1 de la courbe , le point d'ordonnée 3,15 V a pour abscisse 1 s , d'où t1= 1 s .
3/t1 = R1C1 d'où R1= 1/C1=1/10-3 = 1000 W .Et comme R1=R2 , nous avons également R2 =1000 W
4/Pour déterminer t2 , on utilise la partie 3 de la courbe : l'abscisse du point d'ordonnée 3,15 V est égal à t2 = 2 s .
5/ Des deux condensateurs , le premier chargé sera celui qui se trouve dans le circuit dont la constante de temps est la plus faible : c'est donc C1 .
6/Durée de charge de C1 : Dt1 = 5 t1 = 5 s
Durée de charge de C2 : Dt2 = 5 t2 = 10 s .
C/Course à la décharge :
1/ La courbe 2 correspond à la décharge du condensateur de capacité C1 , la courbe 4 à la décharge du condensateur de capacité C2 .
2/Les circuits sont les mêmes que pour la charge : les constantes de temps sont donc les mêmes , c'est à dire :
t1 = 1 s pour le circuit 1 (R1,C1)
t2= 2 s pour le circuit 2 (R2,C2)
3/Sur le graphique , il apparaît que les courbes (2) et (4) se coupe à la date t=2,6 s , autrement dit , à cette date les tensions u1 et u2 sont égales .
4/Sur le graphe il apparaît que le condensateur C1 est déchargé bien avant le condensateur C2 (tensions nulles).
D/Connexion des circuits :
1/Lorsque les condensateurs sont chargés , les tensions à leurs bornes sont respectivement E1=5 V et E2=10 V et par conséquent :
q1 = C1E1= 5.10-3 C = 5 mC
q2=C2E2 = 20 mC
2/ En1= q12/2C1 = 1,25.10-2 J ; En,2= q22/2C2 =0,1 J
3/Si la tension aux bornes de C2 diminue , la charge q2 = C2u2 diminue également . Parallèlement la charge q1 du condensateur C1 augmente : autrement dit , le condensateur C2 se décharge partiellement au profit du condensateur C1 . Ce processus s'explique par le fait que des électrons de l'armature supérieure du condensateur C1 passent sur l'armature supérieure du concensateur C2 et parallèlement , des électrons de l'armature inférieure de C2 passent sur l'armature inférieure de C1 . Le courant est en sens inverse de ce déplacement d'électrons , d'où le schéma indiquant le sens du courant dans le circuit :
4/![]()
5/E'n1= q'12/2C1 =0,034 J ; E'n2 = 6,9.10-2 J
6/En1+En2 = 11,2.10-2 J E'n1+E'n2 = 10,3.10-2 J
IL apparaît que En1+En2 >E'n1+E'n2 : autrement dit , l'énergie n'est pas conservée au cours du processus . Les résistances sont responsables de pertes par effet Joule .
EXERCICE IV : Physique et violon :
1/-1: La direction de perturbation est perpendiculaire à la direction de propagation (celle de la corde) :il s'agit par conséquent d'une onde transversale .
2: Le phénomène observé est un phénomène d'onde stationnaire : Si la longueur de la corde est égale à L et que les extrêmités de la corde sont fixes , alors L=nl/2 , n étant un nombre entier et l est la longueur d'onde .
Avec un seul fuseau n=1 , il s'agit du mode 1 .
3:La caisse en bois du violon permet d'assourer un couplage entre la vibration mécanique de la corde et l'air : elle fait office de caisse de résonance .
2/-1: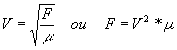
Comme L=l/2 avec l=V/N , N étant la fréquence de l'onde , nous en déduisons :
![]()
3/-1:En appuyant en B , le violoniste modifie la longueur de la corde .
2:La tension F de la corde est telle que : F=4L2N2µ' avec L=55 cm , N=294 Hz (ré3) et µ' la masse linéique de la corde ré3 .
Cette tension est la même lorsque le violoniste appuie en B : F=4L'2N'2µ' avec L'=AB et N'=440 Hz (la3) . Et donc : L2N2=L'2N'2 , ce qui donne L'=36,7 cm .
4/-1:Le son émis par le diapason est un son pur (sa fréquence est celle du fondamental) : ce cas correspond au spectre 1 .Le son émis par le violon n'est pas pur et contient donc des harmoniques : le spectre du son émis par le violon est le spectre 2 .
2:Avec un fondamental de 440 Hz , les différents harmoniques ont pour fréquences F2 = 2*440=880 Hz , F3=1320 Hz , F4= 1760 Hz , F5 = 2200 Hz , F6=2640 Hz .
Les harmoniques 2 (F2) , 4 (F4) et 6 (F6) ne figurent pas dans le spectre du violon .
5/Le niveau sonore mesuré par le sonomètre lorsque les deux élèvent jouent du violon est :
![]() où I est l'intensité sonore provenant d'un seul violon .
où I est l'intensité sonore provenant d'un seul violon .
Exploitant une propriété de la fonction logarithme , nous en déduisons :
![]() (L=70 dBA)
(L=70 dBA)
6/Nous remarquons que le nombre de demi-tons pour passer de sol 2 à ré3 , de ré3 à la3 ou de la3 à mi4 est le même dans les trois cas (7 demi-tons) . Cela signifie que le rapport de la fréquence supérieure sur la fréquence inférieure est le même dans les trois cas .
Cela signifie que f2/f1 = f3/f2 = f4/f3 et
donc ![]()
Exercice 5 : Echographie .
1/-a : Le principe de l'échographie est basé sur la transmission et la réflexion des ondes ultrasonores : "les ondes ultrasonores se propagent et se réfléchissent dans les tissus .
b:Un examen échographique n'utilise pas toujours la même fréquence : la fréquence dépend des organes à explorer .
c:Les ondes ultrasonores sont des ondes mécaniques longitudinales .
d:La fréquance des ondes ultrasonores est supérieure à 20 kHz alors que celle des ondes sonores est inférieure à 20 kHz.
2/-a: l'oscillogramme du dessus représente le signal de l'émetteur . Le signal émis par l'émetteur parcourt une distance égale à 2 d avant de parvenir au récepteur : d'où le décalage temporel entre les deux signaux .
On note de plus un amortissement du signal reçu par le récepteur par rapport au signal émis par l'émetteur .
b:En divisions , le décalage entre les deux signaux est égal à 2,2 divisions . Comme la sensibilité de la base de temps est égale à b=1 ms/div , nous en déduisons la durée Dt entre l'émission et la réception de l'onde : Dt=b.Dx = 1*2,2=2,2 ms
c: ![]()
d:2d=V*Dt d'où d =341*2,2.10-3/2=37,5 .10-2 m = 37,5 cm .
e:* la paroi réflechissante modélise l'organe
* La peu du patient se trouverait au contact de l'émetteur .
* La sonde n'est pas la même : Pour l'échographie , l'émetteur et le récepteur sont dans le même "boitier "
3/-a1: Les deux courbes sont décalées car les ondes émises par l'émetteur ne parviennent pas en même temps aux deux récepteurs qui sont décalés l'un par rapport à l'autre .
a2:Si les coefficients d'amplification des deux voies étaient identiques , le récepteur R2 relié à la voie B étant plus éloigné de l'émetteur que R1 relié à la voie A , on observerait en voie B un signal d'amplitude plus faible que celui observé en voie A à cause de l'amortissement des ondes ultrasonores .
Or il apparait sur l'écran de l'oscillographe que l'amplitude est plus importante en voie B qu'en voie A . Autrement dit , le coefficient d'amplification de la voie B est nécessairement plus élevé que celui de la voie A.
b:DxT = 5 div ; T=b*DxT = 5*5 = 25 µs
f=1/T = 1/25.10-6 = 40000 Hz=40 kHz .
c1-Si on éloigne R2 de R1 , on observe sur l'écran un défilement d'une sinusoïde par rapport à l'autre .Les deux sinusoïdes sont en phase lorsque la distance entre les deux récepteurs est égale à un multiple de la longueur d'onde .
c2:c'est la périodicité spatiale (l) de l'onde qui est mise en évidence .
c3: L=10l d'où l=L/10=8,5/10=0,85 cm =8,5 mm .
l= V*T d'où V=l/t=8,5.10-3/25.10-6 = 340 m/s . Cette valeur est bien la même (aux incertitudes de mesure près) que celle trouvée précedemment par le calcul (341 m/s)