SCIENCES PHYSIQUES - BACCALAUREAT BLANC 2003
LYCEE FREDERIC CHOPIN
Durée de l'épreuve : 3h 30
Calculatrices autorisées
Exercices à traiter par les élèves :
* Spécialité physique-chimie : Exercices I, II , IV et V
* Spécialités Mathématiques et SVT : Exercices I , II , III, IV
I/ DANS UN REACTEUR NUCLEAIRE
Données :
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
Masses de quelques noyaux ou particules :
Nom |
Uranium 235 |
Krypton 90 |
Baryum 142 |
neutron |
Masse en u |
235,043 91 |
89,919 72 |
141,91635 |
1,00866 |
1 u = 931,5 MeV.c-2 = 1,66 10-27 kg ; 1 eV = 1.6.10-19 J ;
Constante d’Avogadro NA = 6,023.1023 mol-1.
Masse molaire de l’uranium 235 : 235 g/mol
I/ - Pour le démarrage d’un réacteur nucléaire à fission, on peut utiliser une source d’américium béryllium. L’américium 241 radioactif est un émetteur a . Une particule a peut réagir avec un noyau 9zBe de béryllium 9 pour produire un neutron 10n et un noyau de carbone 126C.
a)Rappeler les lois utilisées pour équilibrer une équation bilan de réaction nucléaire.
b)Ecrire avec les symboles nucléaires A et Z, les équations bilan :
*de la désintégration de l’américium 241,
*de la transformation du Béryllium 9. En déduire le nombre z .
II/ A la suite d’une collision avec un neutron lent, dans le réacteur un noyau d’uranium peut donner la fission suivante :
235
92U + 10n ® 9036Kr + 142xBa + y 10n1)Déterminer x et y
2)Pourquoi la source de neutrons américium-béryllium est-elle seulement utile au démarrage du réacteur nucléaire ?
3)Calculer en MeV puis en joules l’énergie libérée par la fission d’un noyau d’uranium 235.
4)Calculer l’énergie, en joules, l’énergie libérée par 1 kg d’uranium.
5)Un réacteur nucléaire a une puissance constante de 100 MW. Calculer la durée Dt nécessaire pour consommer 1 kg d’uranium 235 dans ce réacteur.
II/Circuit RLC :
Le montage suivant permet l'étude expérimentale des oscillations libres d'un circuit RLC.
I/Un ordinateur muni d'une carte d'acquisition permet d'enregistrer l'évolution des tensions aux bornes du condensateur C et de la résistance R. Le condensateur étant prélablement chargé sous la tension E, l'interrupteur est basculé en position 2. C'est à ce moment que commence l'acquisition des données .

1-Quelle est la tension visualisée sur la voie 1 ?
2-Quelle est la tension visualisée sur la voie 2 ?
II/On se place dans le cas idéal où la résistance totale de la branche comportant la bobine est nulle .
1-Etablir l'équation différentielle vérifiée par q=qA (charge portée par l'armature A du condensateur )
2-En déduire la période T0 des oscillations .
III/Dans la pratique, la résistance totale de la branche comportant la bobine n'est pas négligeable . On réalise trois expériences afon d'étudier l'influence des différents paramètres des oscillations .
Les graphiques a, b, c (ci-après) représentent les variations de la tension uAB et de l'intensité i du courant dans le circuit .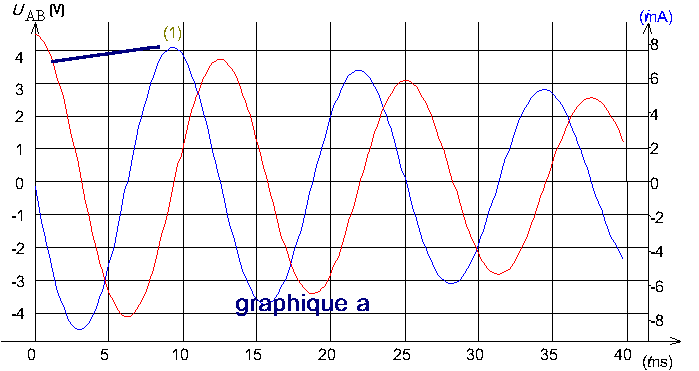
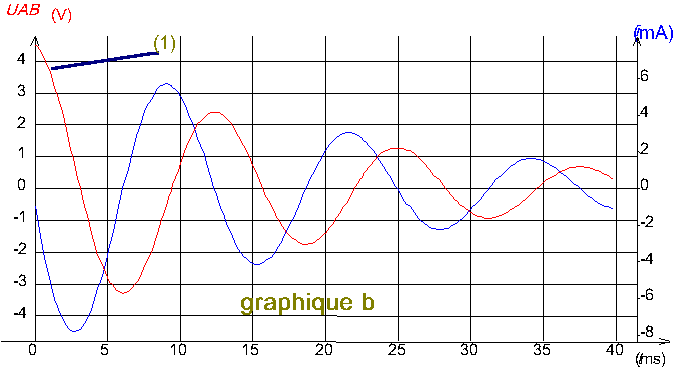
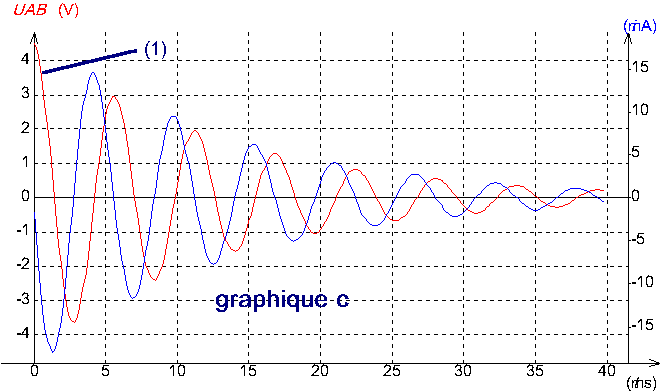
Pour les trois graphiques , la courbe notée 1 , correspond à la tension et l'autre à l'intensité .
1-Calculer les périodes propres T01 , T02 , T03 correspondant à chaque expérience E1 ,E2 et E3 .
2-Mesurer graphiquement la période des oscillations sur les graphiques a,b et c (il s'agit en fait d'une pseudo-période, durée séparant deux passages successifs dans le même sens de la tension uAB par la valeur zéro ; dans les conditions des expériences réalisées , on peut confondre les valeurs numériques de la pseudo-période et de la période propre).
3-Faire correspondre chaque graphique (a-b-c) à une des trois expériences (E1 - E2 - E3 ) en le justifiant .
IV/Le graphique ci-après visualise les énergies emmmagasinées par le condensateur et la bobine en fonction du temps ainsi que leur somme , au cours de l'expérience E1 .
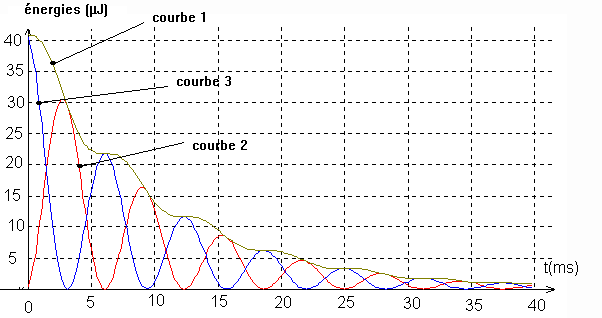
1-Après avoir rappelé les expressions littérales des énergies emmmagasinées par le condensateur EC et par la bobine EL, identifier les trois courbes . Justifier votre choix .
2-Pourquoi la somme des énergies emmagasinée par le condensateur et la bobine est-elle décroissante ?
3-Evaluer l'énergie dissipée pendant les dix premières millisecondes .
Données :
E = 4,5 V ; R variable ; r=14 W ; C variable ; L variable .
Expériences |
R (W) |
L(H) |
C (µF) |
E1 |
100 |
1 |
4 |
E2 |
30 |
0,2 |
4 |
E3 |
30 |
1 |
4 |
III/Dosage d'un détartrant pour cafetière.
(Uniquement pour les élèves des spécialités Maths et SVT)
Données:
Masses molaires en g.mol-1
H : 1 ; O :16 ; N : 14 ;S : 32
Zone de virage des indicateurs colorés:
hélianthine : pH de 3,1 à 4,5
bleu de bromothymol : pH de 6 à 7,6
phénolphtaléine : pH de 8,2 à 10
Un détartrant pour cafetière vendu dans le commerce, se présente sous la forme d'une poudre blanche, l'acide sulfamique H2N-SO3H que l'on notera AH dans l'exercice.
1 / Cet acide réagit avec l'eau par une transformation totale. Ecrire l'équation de la réaction de cette transformation.
2 / On désire déterminer le pourcentage massique d'acide dans le détartrant, pour cela on réalise un dosage pHmètrique.
On réalise d'abord une dissolution. On dissout 1,5 g de détartrant dans un peu d'eau distillée contenue dans une fiole jaugée de 200 mL , puis on complète avec de l'eau distillée jusqu'au trait de jauge. Après agitation, cette solution A a une concentration CA en soluté AH.
On titre un volume VA = 20,0 mL de solution A par une solution aqueuse d'hydroxyde de sodium de concentration CB = 0,10 mol.L-1 . La courbe de titrage est représentée ci-dessous.
a ) Faire un schéma annoté du titrage.
b ) Déterminer graphiquement les coordonnées du point d'équivalence acido- basique.
c ) Quel serait l'indicateur coloré à utiliser si on réalisait un titrage colorimétrique? Justifier la réponse.
3 / Ecrire l'équation de la réaction de titrage (titrage d'une solution d'acide qui réagit totalement avec l'eau) par la soude .
4 / a ) Pour l'équivalence, faire le tableau d'avancement de la réaction en utilisant les quantités de matière.
b ) Définir l'équivalence du titrage acido-basique.
c ) En déduire la concentration CA de la solution A.
5 / Quel est le pourcentage massique d'acide sulfamique dans le détartrant?
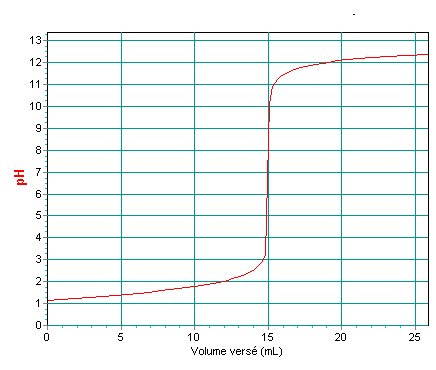
Courbe de titrage
6 / On souhaite vérifier que la réaction de titrage est une réaction totale .Pour cela on fait l'étude d'un point particulier du titrage où le volume VB = 12 mL.
a ) Faire le tableau d'avancement de la réaction en utilisant les quantités de matière. Quel est le réactif limitant?
b ) En déduire l'avancement maximal xm.
c ) A l'aide de la mesure du pH (lu sur la courbe) , déterminer la quantité de H3O+ à l'état final nf (H3O+).
d ) En utilisant les connaissances ci-dessus, donner l'expression littérale de l'avancement final xf et calculer sa valeur.
e ) En déduire le taux d'avancement final de la transformation. Conclure.
IV/ETUDE CINETIQUE PAR CONDUCTIMETRIE
Dans cet exercice, on s'intéresse à la réaction d'oxydoréduction entre les ions peroxodisulfate S2O82- et les ions iodure I- en solution aqueuse.
Donnée : Couples oxydant / réducteur : S2O82- / SO42- et I2 / I-
Dans un bécher, on introduit un volume V1 = 40 mL d'une solution aqueuse de peroxodisulfate de potassium (2K++S2O82-) de concentration C1 = 1,0 . 10-1 mol/L. A l'instant t = 0 s, on ajoute un volume
V2 = 60 mL d'une solution aqueuse d'iodure de potassium (K++I-) de concentration C2 = 1,5 . 10-1 mol/L.
Un conductimètre, relié à un système d'acquisition de données, permet de suivre l'évolution de la conductance de la solution au cours du temps. La courbe obtenue est reproduite ci-dessous.
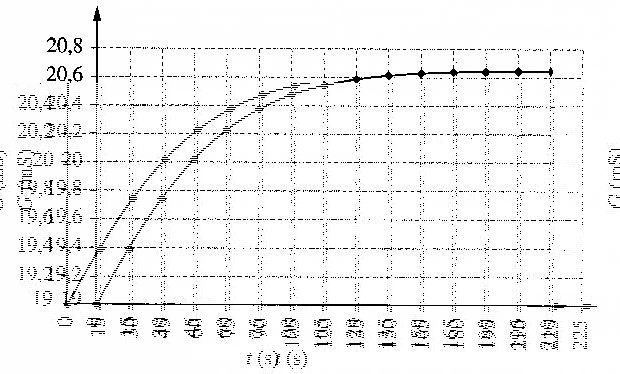
1. Ecrire les demi-équations pour chacun des deux couples qui interviennent dans cette réaction d'oxydoréduction.
2. En déduire l'équation de la réaction entre les ions peroxodisulfate et les ions iodure.
3. a)Faire un tableau d'avancement de la réaction. On notera x l'avancement molaire (quantité de matière) de la réaction à l'instant t.
b)Recenser les espèces ioniques présentes en solution, puis donner les expressions littérales des concentrations des divers ions présents dans le mélange en fonction de x et du volume VT de la solution. On négligera les ions H3O+ et OH- très minoritaires devant les autres ions.
4. On rappelle que la conductance G d'une telle solution a pour expression :
G = k(2![]() +
+ ![]() + 2
+ 2![]() +
+ ![]() )
)
où les li sont les conductivités molaires ioniques (qui ne dépendent que de l'ion et de la température) et k la constante de cellule.
Montrer que la relation entre la conductance G et l'avancement x de la réaction est de la forme :
![]() où VT est le volume total de la solution exprimé en
litres , constant pendant toute la durée de l'expérience.
où VT est le volume total de la solution exprimé en
litres , constant pendant toute la durée de l'expérience.
Pour la suite de l'étude, on donne les valeurs des constantes (dans les conditions de l'expérience) :
A = 1,9 mS.L et B = 42 mS.L.mol-1.
5.a)Donner l'expression de la vitesse volumique v de la réaction en fonction de l'avancement x. En déduire l'expression de v en fonction de G.
b) A l'aide du graphe, expliquer comment évolue la vitesse de la réaction au cours du temps. Proposer une explication.
6. A l'aide du graphique, déterminer la valeur de la vitesse volumique v à la date t = 1 min.
7.Déterminer la valeur xmax de l'avancement maximum de la réaction et en déduire Gmax , la valeur maximale de G .
8. En utilisant le résultat de la question précédente, déterminer graphiquement l'instant à partir duquel on
peut considérer que la réaction est finie.
V/DOSAGE DES IONS CHLORURE PAR LA METHODE DE CHARPENTIER-VOLHARD
(Uniquement par les élèves de la spécialité SPC)
Le but de cet exercice est de doser les ions chlorure effectivement présents dans un sachet de soupe déshydratée poireaux-pommes de terre. On ne tiendra pas compte des autres ions apportés par la matière sèche.
Protocole opératoire
On dissout le contenu du sachet dans 50 cm3 d'eau tiède. (On considère que tous les ions passent en solution).
On filtre les résidus solides (poireaux, pommes de terre...) et le filtrat est complété à 1,0 L par de l'eau.
Etape 1 : On prélève 10,0 cm3 de filtrat qu'on place dans un erlenmeyer. On y ajoute un excès de nitrate d'argent (Ag++NO3-), soit un volume V1 = 20,0 cm3 de solution de nitrate d'argent de concentration
c1 = 1,0.10-1 mol/L. Les ions Ag+ introduits en excès précipitent avec les ions chlorure. Soit A le mélange ainsi constitué.
1.a) Qu'observe-t-on dans l'erlenmeyer ? Ecrire l'équation de la réaction correspondante.
Cette réaction sera par la suite notée R1. La transformation chimique associée à R1 sera considérée comme totale
b) Faire le tableau d'avancement de la réaction R1, on appellera x l'avancement molaire. Exprimer, dans l'état final, la quantité de matière des ions chlorure et argent en fonction de l'avancement x.
Etape 2 : Les ions argent restant dans A sont ensuite dosés en milieu acide par des ions thiocyanate SCN-
(introduits par le thiocyanate de potassium (K++SCN-) de concentration c = 1,0.10-2 mol/L), en présence d'un indicateur de fin de réaction constitué d'ions ferrique Fe 3+. Deux réactions successives se produisent:
Ÿ Les ions argent réagissent d'abord avec les ions thiocyanate pour donner un précipité blanc de thiocyanate d'argent. Cette réaction servant de support au dosage sera par la suite notée R2
Ÿ Lorsque tous les ions argent présents dans l'erlenmeyer ont précipité avec les ions SCN-, alors les ions Fe 3+ réagissent avec les ions thiocyanate pour former un ion complexe rouge Fe(SCN)2+. L'apparition de ce complexe rouge indique que l'équivalence a eu lieu.
2.a) Faire le schéma annoté du dosage réalisé à l'étape 2.
b) Ce dosage a lieu en milieu acide ; on dispose au laboratoire d'acide nitrique (H++NO3-) et d'acide chlorhydrique. Lequel choisir ? Pourquoi ?
c) Parmi les qualificatifs suivants, choisir ceux qui se rapportent au dosage réalisé :
Ÿ direct Ÿ indirect Ÿ conductimétrique Ÿ acidobasique Ÿ par précipitation Ÿ pH-métrique
d) Ecrire l'équation de la réaction à laquelle participent les ions Fe3+ et servant d'indicateur de fin de la réaction R2.
3. a) Ecrire l'équation de la réaction R2 servant de support au dosage.
b) Donner la définition de l'équivalence.
c) Etablir le tableau d'avancement de la réaction R2, en appelant x' l'avancement molaire de cette réaction.
4. L'équivalence a lieu pour un volume de thiocyanate de potassium versé v égal à 17,0 cm3. En déduire le nombre de moles d'ions argent qui restaient dans l'erlenmeyer à l'issue de l'étape 1, dans la solution A.
5.a) En déduire alors la quantité d'ions chlorure initialement présents dans les 10,0 cm3 de filtrat de
l'étape 1.
b) D'après les indications portées sur le sachet, ce dernier contient 98 g de matière déshydratée, dont 11 % en masse de chlorure de sodium (Na++Cl-). Donnée : M Cl = 35,5 g/mol M Na = 23 g/mol
Déterminer la quantité d'ions chlorure contenue dans un sachet de soupe, d'après les indications du fabricant.
c) Comparer le résultat expérimental à la quantité d'ions chlorure supposés être présents, d'après les indications du fabricant, dans les 10,0 cm3 placés dans l'erlenmeyer. Conclure.
CORRECTION :
I/Réacteur nucléaire :
I/a-Conservation du nombre de nucléons et de la charge .
b)
![]()
![]() . La conservation de la charge
donne z= 4
. La conservation de la charge
donne z= 4
II/
1) x= 56 y = 4
2)La réaction de fission produit des neutrons et ceux-ci vont engendrer d'autres réactions de fission , si bien que la réaction d'amorçage n'est plus nécessaire .
3)
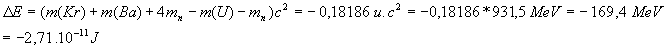
4)1 kg d'uranium contient 1000/(235)*6,02 1023 = 2,56 1024 atomes . L'énergie libérée par atome d'uranium étant de 2,7 10-11 J , 1 kg d'uranium libère par conséquent E= 6,94 1013 J .
5) E = P Dt d'où Dt = 694220 s = 8 jours .
II/Circuit RLC
I/-1 : on visualise uc en voie 1
2 : on visualise uR ou i (à une constante multiplicative près) en voie 2 .
II/-1: En prenant les notations du schéma , avec uR=0 puisque R=r=0 , nous pouvons écrire :
![]()
Comme , de plus i=dq/dt , nous obtenons
finalement : ![]()
2 : l'équation diférentielle est
caractéristique d'un oscillateur (non amorti) de pulsation ![]() d'où la période propre
d'où la période propre ![]()
III/-1 T01 = 12,5 ms ; T02 = 5,6 ms ; T03 = 12,5 ms
2- Ta = 13 ms ; Tb = 13 ms ; Tc = 6 ms
3- il est clair que c correspond à E2 . Pour les courbes a et b , elles ont toutes les deux la même pseudo-période , mais pour le graphique b , l'amortissement est plus important , ce qui correspond à E1 , puisque c'est dans cette expérience que la résistance est la plus élevée .
Finalement , le graphique a correspond à E3 .
IV/-1 : EC = 1/2 C.uc2 et EL =1/2 Li2.
Ces deux expressions ont notamment pour conséquence que EC s'annule avec uC et EL s'annule avec i . Aussi en comparant le graphique b (expérience E2) au graphique des énergies , nous pouvons affirmer :
* la courbe 3 correspond à EC
*La courbe 2 correspond à EL
* La courbe 1 est la somme des deux autres et correspond par conséquent à E=EC + EL .
2 : E est l'énergie totale du circuit RLC . A cause des pertes par effet Joule , celle-ci diminue .
3: E(0) = 40 µJ et E(10 ms) = 13 µJ : l'énergie dissipée pendant les 10 premières millisecondes est donc égale à 27 µJ .
III/Détartrant :
1/AH + H2O ---> A- + H3O+
2/
a)bécher(solution acide-détartrant) , burette ( solution de soude 0,1 mol/L), agitateur magnétique, pH-mètre . Il faut faire les shémas et indiquer contenants et contenus.
b)méthode des tangentes :E (Vb,e= 15 mL , pH=7)
c)BBT : zone de virage contient le point d'équivalence
3/H3O+ + HO- --> 2 H2O (titrage d'une solution d'acide fort ) .
4/
a)
| H3O+ + HO- = 2 H2O | ||||
| EI X=0 | CAVA | CBVB,equiv | excès | |
| EF X=Xf | CAVA - Xf | CBVB,equiv - Xf | excès | |
b)A l'équivalence , les réactifs ont totalement réagi et donc CAVA - Xf = CBVB,equiv - Xf
En éliminant Xf , nous obtenons : CAVA = CBVB,equiv
CA = 0,1* 15/20 = 0,075 mol/L
5/La masse d'acide sulfamique contenue dans 200 mL est mar conséquent m= CA*0,2*(2+14+32+3*16+1)=1,455 g ce qui correspond à un pourcentage de 1,455/1,5 = 97 %
6/
a)
| H3O+ + HO- = 2H2O | ||||
| EI X=0 | CAVA | CBVB,12 | excès | |
| EF X=Xf | CAVA - Xf | CBVB,12 - Xf | excès | |
VB=12 mL < 15 mL est situé avant l'équivalence : le réactif limitant est par conséquent ici , la solution titrante de soude .
b)Xmax correspond à la valeur de l'avancement lorsque le réactif limitant a complètement disparu et donc CBVB,12 - Xmax = 0 . Nous obtenons donc Xmax = 0,1 * 12 10-3 = 1,2 10-3 mol .
c)nf(H3O+) = [H3O+]*(VA+VB,12) = 10-pH *(VA+VB,12)
Sur la courbe , on lit pH=2 et donc nf(H3O+) = 3,2 10-4 mol .
d)nf(H3O+) = CAVA - Xf , d'où Xf = -3,2 10-4 + 0,075*20 10-3 = 1,2 10-3 mol
e)t = Xf/Xmax = 1 : la réaction de titrage est bien totale .
IV/ Cinétique :
1/S2O82- + 2e = 2SO42- et I2 + 2e = 2I-
2/S2O82- + 2I- = I2 + 2SO42-
3/ a)
| S2O82- + 2I- = I2 + 2SO42- | ||||
| EI X=0 | C1V1 | C2V2 | 0 | 0 |
| A l'instant t X | C1V1 - X | C2V2 - 2 X | X | 2X |
| Etat final Xmax=0,004 | 0 | 0,001 | ||
b) espèces : S2O82- , SO42- , I2 , I- , K+ et H2O . espèces ioniques :S2O82- , SO42- ,I- , K+
[S2O82-] = (C1V1 - X)/VT ; [SO42-] = 2X/VT ; [I-] = (C2V2 - 2X)/VT ; [K+] = (2C1V1 +C2V2)/VT
4/ G=k/VT * [2l1*(C1V1 -X) +l2*(C2V2-X) +2l3*2X + l4*(2C1V1+C2V2)]
= 1/VT * ([2kl1C1V1 + kl2C2V2 +2kl4C1V1+kl4C2V2] + (4kl3 - 2kl1 - 2kl2) X)
Si nous posons :
A = [2kl1C1V1 + kl2V2C2 +2kl4C1V1+kl4C2V2]
B = (4kl3 - 2kl1 - 2kl2)
cela correspond bien à l'expression donnée dans l'énoncé .
5)-a: v= 1/VT dX/dt
d(G)/dt = B/VT * dX/dt = B*v d'où v= 1/B dG/dt
b- v est égale à une constante multiplicative positive près égale au coefficient directeur de la tangente à G(t) . Or la pente de la tangente diminue au cours du temps . v est donc une fonction décroissante du temps .
Ce résultat est en accord avec le fait que v est une fonction croissante des concentrations des réactifs (facteur cinétique) . Or ici , les réactifs réagissant entre eux , leur concentration diminue au cours du temps et par conséquent v diminue également .
6/ v= 1/42* 0,4/30 = 3,1 10-4 mol.L-1.s-1 .
7/ Xmax = 0,004 mol et Gmax = 20,6 mS
8)La réaction est terminée lorsque G=Gmax c'est à dire à t=135 s (environ).
V/Dosage des ions chlorure :
1-a :Dans l'erlenmayer on observe un précipité blanc de chlorure d'argent AgCls suivant la réaction :
Ag++Cl- ------> AgCls . (R1)
b:
| Ag+ + Cl- = AgCls | ||||
| EI X=0 | C1V1 | n0(Cl-) | solide | |
| EF X=Xf | C1V1 - Xf | n0(Cl-) - Xf | solide | |
Les ions Ag+ ont été introduits en excès et par conséquent , à l'état final :
nf(Cl-) = 0 d'où Xf = n0(Cl-) et donc
nf(Ag+) = C1V1 - n0(Cl-) .
2/-a : burette , bécher , réactifs et agitateur magnétique .
b :il faut prendre l'acide nitrique . L'utilisation d'acide chlorhydrique introduirait des ions Cl- , qui sont précisément les ions que nous voulons doser .
c: direct - par précipitation
d: Fe3+ + SCN- = Fe(SCN)2+
3/-a: Ag+ + SCN- = AgSCNs
b:A l'équivalence , les réactifs ont été mélangés dans les proportions stoechiométriques de la réaction support du dosage .
c:
| Ag+ + SCN- = AgSCN | ||||
| EI X=0 | n'0 (Ag+) | CV | solide | |
| EF X=Xf | n'0(Ag+) - X'f | CV - X'f | solide | |
4/ A l'équivalence : n'0(Ag+) - X'f = CV - X'f = 0
d'où n'0(Ag+)= CV
5/-a: il est clair qu'ici n'0(Ag+) = nf(Ag+) et donc :
n0(Cl-) = C1V1 - CV = 0,1 * 20 10-3 - 10-2 * 17 10-3 = 18 10-4 mol .
b: n(Cl- fabricant ) = 98*0,11/78,5 = 0,14 mol soit 14 10-4 mol dans 10 mL de filtrat