
Exercice 1 page 58 :
a : F ; b:F ; c:V (3eme harmonique - 3 ventres et 4 noeuds)
Exercice 2 page 58 :
a : F ; b:V ; c:F
Exercice 3 page 58 :
Le nombre de ventres est proportionnel à la fréquence (L=nl/2 = n/2 * c/f) d'où n=(2L/c)*f )
325*3/2= 487
a:F ; b:F ; c:V
Exercice 10 page 58 :
1/ les deux points fixes de la corde sont situés aux extrêmités au niveau du sillet et du chevalet .
2/T1 = 2,3 ms d'où f1 = 434 Hz
3/Tous les points de la corde vibrent à la même fréquence temporelle :celle du fondamental .
4/La vibration temporelle n'est pas sinusoïdale (elle est toutefois périodique) :les trois vibrations comportent par conséquent des harmoniques (penser au théorème de Fourier).
Exercice 11 page 59 :
1/ *premier spectre : une seule composante . Il s'agit du spectre du son émis par le diapason .
* deuxième spectre : constitué du fondamental et d'harmoniques : clarinette .
2/T1=2,27 ms donne f1 = 440 Hz . Cette valeur correspond bien à celle du fondamental du spectre fréquentiel pour les deux sons .
3/les fréquences fj des harmoniques sont telles que fj = j*f1 j=2 , 3 , 4........... , ce qui correspond aux fréquences en Hz : 880 , 1320 , 1760 , 2200 .......
4/A partir du spectre fréquentiel de la clarinette nous constatons que les harmoniques 1 à 6 sont présents dans le son émis par la clarinette .
5/La caisse de résonance transmet les vibrations à l'air ambiant .
6/-a : l'hypothèse formulée revient à affirmer que l'air n'est pas un milieu dispersif (vitesse de propagation indépendante de la fréquence).
b-l= 340 /f1 = 0,77 m = 77 cm
c- l2 =340/2f1 = 38,5 cm
Exercice 13 page 60
1/

6 ventres
2/La corde vibre selon le mode de l'harmonique 6
3/f6=100 Hz f1= 100/6 = 16,6 Hz
4/-a : En changeant la masse , on fait varier la célérité le long de la corde et par conséquent la longueur d'onde change également (elle devient l') et si la longueur de la corde n'est pas telle que L=nl'/2 , il n'y a plus de phénomène d'ondes stationnaires .
b: f1 = 100 /7 = 14,3 Hz
c:On peut montrer que pour une longueur de corde donnée , la fréquence du fondamental augmente avec la tension de la corde (f1 = V/2L , V augmente avec la tension de la corde) .
Or, ici , la longueur de la corde varie : l'expérience réalisée ne permet pas par conséquent de conclure.
Exercice 1 page 73 :
a: V ; b:F ; c:F
Exercice 2 page 73 :
a:F ; b:V ; c:F
Exercice 3 page 73 :
a : V ; b:F ; c:F (voir exercice précédent)
Exercice 6 page 73 :
a:V ; b:V ; c:F (réponse b : entre 2 noeuds successifs)
Exercice 7 page 73 :
1)Amplitude de l'onde réfléchie : A (on suppose qu'il n'y a pas d'amprtissement) . Sa pulsation est la même que celle de l'onde incidente : w .
2/l= cT = c*2p/w . C'est la même que celle de l'onde incidente .
Exercice 12 page 74 :
L= l/2 (fondamental) ; l=c/f d'où c = l*f = 2L*f=456 m/s
Exercice 19 page 74 :
1/La fréquence du fondamental est égale à la fréquence des oscillations libres de chacune de ces cordes .
2/ La longueur d'onde du fondamental est telle que L=l/2 et par conséquent l=65 cm
3/l=v/f1 ou v=l.f1 : 127 m/s (sol2) ; 191 m/s (ré3) ; 286 m/s (la3 ) ; 428 m/s (mi4)
4/m=T/v2 : 3,7 g/m (sol2) ; 1,64 g/m (ré3) ; 0,73 g/m (la3) ; 0,33 g/m (mi4)
5/masse d'un cylindre de diamètre D et de longueur L=1 m : m= r*(p.D2/4)*1 d'ou 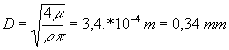
6/On agit sur le réglage de la tension de la corde : on modifie donc v et ainsi f .
Exercice 24 page 76 :
Rectificatif énoncé : c'est le fondamental de la flute soprano qui a une fréquence de 523 Hz
1-a:on souffle dans la flute et on enregistre le son via une ensemble micro et interface d'acquisition . On mesure la période du signal enregistré et on en déduit f1
b:
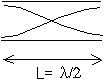
c:Le noeud de vibration se situe au milieu de la colonne d'air (c'est un ventre de pression)
d:L=
l0/2= v/(2f1)e: L= 32,5 cm
f: Les deux valeurs ne sont pas identiques . Ce sont les conditions aux limites qui sont critiquables :il n'y a pas exactement des ventres aux extrêmités.
2-a:Lorsque tous les trous sont bouchés , nous avons des ventres de vibration aux extrêmités (schéma ci-dessus) : d'après ce qui précède la fréquence du fondamental est inversement proportionnelle à L (f peut se mettre sous la forme :f= constante /L).
Tenant compte des "rectificatifs" indiqués à la question précédente , nous pouvons écrire :
f
1,soprano * Lsoprano = f1,alto * Laltod'où f
1,alto = 523 *28,3 /41 = 361 Hz