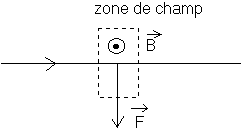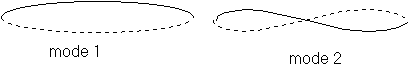TS - SPECIALITE PHYSIQUE
MODES DE VIBRATION - QUANTIFICATION
Les fichiers de simulation sont dans le dossier :Spécialité/Ondes
I/Vibration d'une corde tendue entre deux points :
a)Rappel : Superposition de deux ondes
La perturbation résultante est la somme géométrique des perturbations qui se
rencontrent .
b)Réflexion sur un obstacle fixe :
Reflex.xls - Pour interrompre les simulations appuyer sur "ESC"
Q1)Sur deux schémas , représenter :
a)l'onde incidente
b)l'onde réfléchie
c)Réflexion sur un obstacle libre :
Q2)Question identique à Q1
d)Superposition de deux ondes progressives sinusoïdales :
Onde_stationnaire.xls
1-Obstacle fixe
"Régler" le logiciel
Lancer la simulation (déplacement du curseur "temps")
Q3)Sur un schéma , représenter :
a-l'onde incidente
b-l'onde réfléchie
c-l'onde résultante
Faire apparaître clairement sur le schéma la vérification du principe de
superposition .
2-Obstacle mobile :
Lancer la simulation
Q4)Identique à Q3
3-Ventres et noeuds :
"Régler" le logiciel sur "obstacle fixe "
B et D sont des noeuds de viration
A et C sont des ventres de vibration
Q5)Justifiez les qualificatifs des points A,B,C et D
Q6)Déterminer la longueur d'onde :
a-par le calcul (T est donnée en secondes et v en m/s)
b-par une mesure directe sur l'image de l'écran (utiliser les graduations de l'axe
horizontal)
Q7)Exprimer en fonction de la longueur d'onde l la distance entre deux noeuds successifs .
e)Conditions nécessaires à l'obtention d'ondes stationnaires (modes)
expériences (bureau) : mise en évidence de l'existence de modes
1-Corde de Melde :
Q8)Faire un schéma de la corde à la résonance (ondes stationnaires)
2-Corde de guitare dans un champ magnétique et traversée par un courant
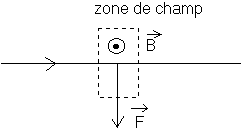
Q9)Faire le schéma de la corde
a-dans le mode 1 : 1 fuseau - fréquence f1
b-dans le mode 2 : 2 fuseaux - fréquence f
2
Conditions de résonance :
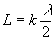 k entier
k entier
ou 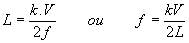
L : longueur de la corde ; V : célérité des ondes le long de la corde ; f :
fréquence de l'onde
f1 :
fondamental (mode 1)
f2 , f3 ......... : harmoniques 2 et
3 .......
Remarque 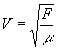 F est la tension de la corde et m la masse par unité de longueur .
F est la tension de la corde et m la masse par unité de longueur .
Q10)Soit f la fréquence du courant qui traverse la corde dans le mode 2. Quelle est
la fréquence de vibration de chacun des points de la corde ?
II/Analyse d'un son d'une corde de guitare :
a)Production d'un son par un instrument de musique :

b)Son émis par une corde de guitare pincée ou frappée :
Q11)Dans le cas d'une guitare , quel est :
* le système mécanique vibrant
* le système de couplage avec l'air
*le milieu de propagation ?
* le récepteur sonore ?
A partir du dossier "LOGICIELS" , lancer "WAVER"
puis : CHARGER "c:\waver\exemples\guitare.wav
JOUER (écoute du son)
Cliquer une fois sur le bouton loupe - :
Q12)Représentez le signal de l'écran en entier sur votre copie .
En maintenant le bouton gauche de la souris enfoncé , sélectionner le signal sur une
durée légèrement supérieure à une période :
Une nouvelle fenêtre s'ouvre . Si la partie sélectionnée dans la nouvelle fenêtre
correspond bien à une période , cliquer "OUI" .
Q13)Quelle est la période du son émis par la guitare ? Quelle est la fréquence
correspondante ?
Cliquer à nouveau sur le bouton "loupe" jusqu'à ce que soit affichée la
valeur 1% (on visualise ainsi la quasi-totalité du signal enregistré)
Q14)Représentez le signal visualisé à l'écran sur votre copie .
c)Analyse harmonique :
Q15)Le son émis par la corde de guitare est-il sinusoïdal ?
Théorème de Fourier : Toute fonction f(t) périodique de période T peut être
mise sous la forme d'une somme de fonctions sinusoïdales :
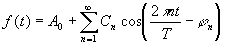 n entier
n entier
n=1 : fondamental
Sur la partie inférieure de la fenêtre du logiciel WAVER est visualisée sous forme
de diagramme en bâtons le spectre du signal (fréquence en abscisse et taille des bâtons
proportionnelle à Cn)
Q16)Représentez le spectre du signal sur votre copie .
Q17)Quelles sont les fréquences :
* du fondamental . Comparer celle-ci à la fréquence du signal précedemment calculée
.
*des harmoniques 2 et 3 ?
Quitter le logiciel (sans rien sauver)
III/Vibrations d'une colonne d'air :
logiciel ONDES_GAX.XLS (bureau)
a)Les paramètres à considérer :
* la pression
* le déplacement des molécules .
ventre de pression <--------> noeud de déplacement
noeud de pression <---------> ventre de déplacement
b)Mise en évidence du phénomène d'ondes stationnaires dans une colonne d'air :
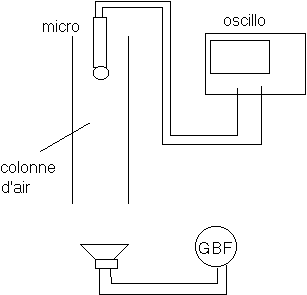
* On fixe la fréquence (GBF) et on déplace le micro à l'intérieur du tube .
* On laisse le micro fixe et on fait varier la fréquence .
Nous mettons ainsi en évidence l'existence de ventres et noeuds de pression pour
certaines fréquences (phénomène de quantification)
Conditions d'obtention du phénomène de résonance :
aux extrêmités : ventres de déplacement (ou noeud de pression)
mode 1 : (déplacement)
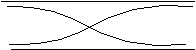
Q18)Exprimer la relation de quantification entre la longueur d'onde l et la longueur L du tuyau pour le mode 1 .
Modes de vibration - Quantification (correction)
1)Obstacle fixe
onde incidente : 
onde réfléchie :
2)Obstacle mobile
onde incidente :
onde réfléchie :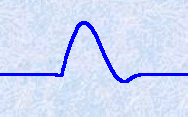
3)Obstacle fixe :
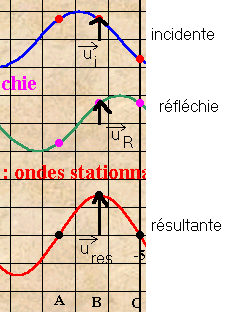
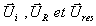 sont les vecteurs
"déplacement" d'un point de la corde par rapport à la position de la corde non
perturbée respectivement dû à l'onde incidente , l'onde réfléchie et l'onde
résultante .
sont les vecteurs
"déplacement" d'un point de la corde par rapport à la position de la corde non
perturbée respectivement dû à l'onde incidente , l'onde réfléchie et l'onde
résultante .
Il apparaît que : 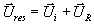 , autrement dit , le principe de
superposition est vérifié .
, autrement dit , le principe de
superposition est vérifié .
4)L'égalité vectorielle de ci-dessus est également vérifiée : dans le cas
particulier du point considéré , nous avons : 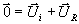
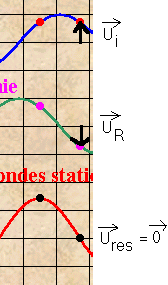
5)B et D sont immobiles (noeuds de déplacement) , les amplitudes d'oscillation de A et
C sont maximales (ventres de déplacement)
6) -a: l= V*T =10 cm/s * 0,5 s =
10 cm
b: La mesure directe sur l'image donne l= 5 divisions = 5 cm
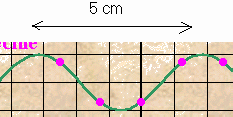
7)Sur le schéma de l'onde résultante , il apparaît que la distance entre deux noeuds
successifs est égale à l/2 .
8) Ondes stationnaires le long de la corde

on observe des fuseaux pour certaines fréquences de vibration du vibreur .
9)
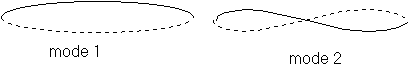
On remarque que l1 = 2l2 et par conséquent f2=2f1
10)Tous les points de la corde vibrent à la même fréquence (sauf les noeuds qui sont
immobiles)
11)corde de guitare :
* système mécanique vibrant : la corde
*système de couplage avec l'air : le caisson
* milieu de propagation : l'air
*récepteur sonore : l'oreille (un micro est aussi un récepteur sonore .
12)
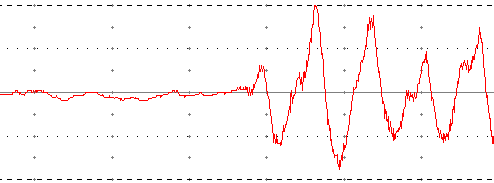
13)T = 7,4 ms f=1/T = 1/(7,4 . 10-3) = 135 Hz
14)Signal complet
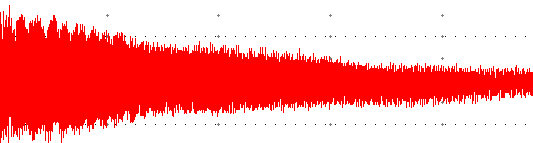
15)Le son émis par la guitare n'est pas sinusoïdal .
16)Spectre du signal :

17) *fondamental : 135 Hz . Cette fréquence est égale à celle précédemment
calculée à partir de la mesure de la période du signal .
*harmonique 2 : 270 Hz = 2*135 Hz
*harmonique 3 : 405 Hz = 3*135 Hz
18) L =l/2 : f1= V/l = V/2L (L est la longueur du tuyau)
19) f2 = 2f1 et f3= 3f1