FILTRAGE - SPECIALITE PHYSIQUE-CHIMIE
I/Objectif :
*Mettre en évidence les fonctions de transfert de différents dipôles
*Déterminer la ou les fréquences de coupure à 3 dB dans chacun des cas .
*Déterminer la fréquence de résonance ou d'anti-résonance s'il y a lieu
II/Branchements :
a)Coté Orphy :
SA : sortie analogique : connecteur H
EA : entrée analogique : connecteur I
EAD : entrée analogique différentielle : connecteur G
b)Coté montage
dépend du montage
Avant de faire le montage et pour toutes les mesures, relier en utilisant les prises arrière sur les fiches mâles :
SA et EA
la masse SA et la masse EA
III/Logiciels :
Les logiciels utilisés sont :
* GBF pour les acquisitions
* REGRESSI pour le traitement des données .
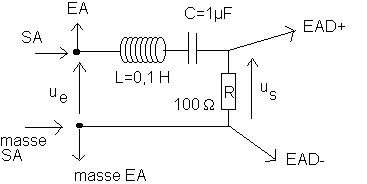
IV/Filtre passe-bande :
a)Montage :
b)Acquisition
Lancer le logiciel GBF (dans Document LOGICIELS)
Configuration/Mode
Choisir Filtre (case à cocher) / Ok
Auto
La courbe Us/Ue ( Ue est la valeur efficace de la tension associée à ue , Us est la valeur efficace de la tension associée à us ) en fonction de la fréquence f est tracée automatiquement à l'écran .
Lorsque le tracé est terminé , cliquer REGRESSI
c)Traitement (Reg 3)
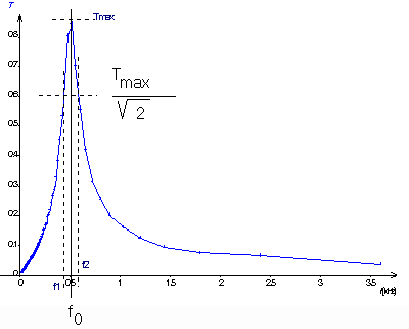
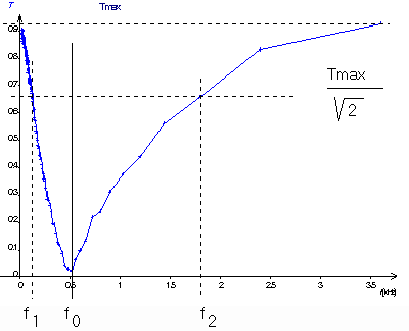
Q1)Utiliser Regressi (Curseur/Reticule) pour déterminer la fréquence de resonance f0 . Comparer à la fréquence propre du dipôle RLC
Q2)Faire le schéma de la courbe 
en fonction
de f sur votre copie .
Considérant la fonction Us/Ue= g(f) , une fréquence fC telle que 
est
appelée fréquence de coupure à - 3dB (lire - 3 décibels) .
Q3)Déterminer les fréquences de coupure à -3dB f1 et f2 du filtre étudié .En déduire la bande passante Df = |f2- f1|
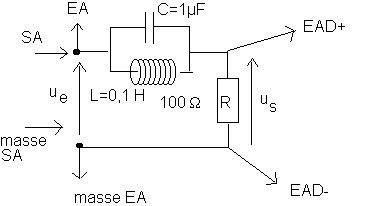
V/Circuit LC Parallèle
Réduire la fenêtre principale de Regressi en cliquant sur l'icône 
: La fenêtre de GBF réapparait alors à l'ecran
Fichier/RAZ
a)Montage :
Démonter compètement le circuit précédent et réalisez le montage suivant :
b)Acquisition
Auto
Lorsque le tracé est terminé , cliquer REGRESSI /Nouvelle page
c)Traitement (Reg 3)
Q4)Utiliser Regressi (Curseur/Reticule) pour déterminer la fréquence d'anti- résonance f0 qui est la valeur de f pour laquelle la fonction observée est minimale .. Comparer à la fréquence propre du dipôle RLC correspondant .
Q5)Déterminer les fréquences de coupure à -3 dB , f1 et f2 . (On cherche
f1 telle que 
) et la bande
de coupure 
Q6)Faire le schéma de la courbe en fonction
de f sur votre copie .
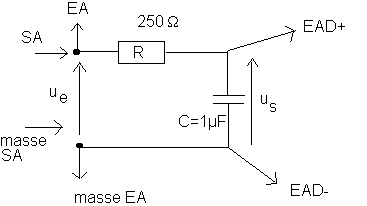
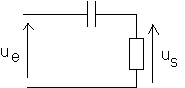
VI/Filtre RC Passe - bas
Réduire la fenêtre principale de Regressi en cliquant sur l'icône : La fenêtre de GBF réapparait alors à l'ecran
Fichier/RAZ
a)Montage :
Démonter compètement le circuit précédent et réalisez le montage suivant :
b)Acquisition
Auto
Lorsque le tracé est terminé , cliquer REGRESSI /Nouvelle page
c)Traitement (Reg 3)
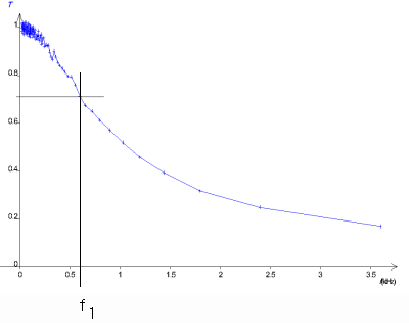
Q7)Utiliser Regressi (Curseur/Reticule) pour déterminer la fréquence
f1 de coupure à -3 dB . (On cherche f1 telle que 
).
Comparer à 1/2pRC
Q8)Faire le schéma de la courbe en fonction
de f sur votre copie .
VII/Filtre passe-haut
Q9)Que peut-on dire d'un condensateur lorsqu'il est traversé par un courant haute fréquence ?
Q10)Par un raisonnement physique essayez de prévoir la réponse T(f) du filtre obtenu en permutant dans le circuit précédent R et C . Faites en le schéma sur votre copie .
VIII/Spectre d'un signal filtré par un filtre passe-bas :
On se propose de simuler l'effet du filtre passe-bas étudié plus haut sur un signal périodique constitué de 3 harmoniques (fondamental et les harmoniques 2 et 3) en utilisant Regressi .
a)Le simulateur :
Q11)Dans le cas du circuit RC construit plus haut , montrer que :
Regressi utilisera cette équation différentielle pour simuler le filtre passe-bas .
b)Le signal d'entrée ue
fondamental : 200 Hz ; harmonique 3 : 300 Hz ; harmonique 5 : 1000 Hz
Lancer Regressi (Bureau/Regressi/Regressi)
Fichier/ouvrir/filtrepb.rw3
Q12)Afficher la courbe ue = f(t) (Reg 3 et Reg 4) et représentez la sur votre copie
Q13)Afficher le spectre de ue (Reg 9). S'assurer qu'il s'agit bien du spectre de ue ,sinon (Reg 10) . Réaliser un zoom sur l'intervalle [0;1500 Hz] (Reg 11). Représentez le spectre sur votre copie .Commentez
c)Le signal de sortie us
Q14)Afficher la courbe us = f(t) (Reg 3 et Reg 4) et représentez la sur votre copie . Comparez la à ue(t)
Q15)Afficher le spectre de us (Reg 9). S'assurer qu'il s'agit bien du spectre de ue ,sinon (Reg 10) . Réaliser un zoom sur l'intervalle [0;3500 Hz] (Reg 11). Représentez le spectre sur votre copie .
Q16)Comparez le spectre de us à celui de ue . Faites le lien avec la courbe obtenue expérimentalement à la question Q8 .Quelle est l'influence du filtre ?
FILTRAGE : Correction
1)f0=504 Hz . A
comparer avec :
(fréquence propre
théorique)
2)
Attention : ne pas confondre les minuscules et les majuscules :
u
e(t) est la tension instantanée et d'épend du tempsU
e est la valeur efficace de ue (
où Ue,m est l'amplitude de ue(t))
3)f
1= 454 Hz f2= 568 Hz Df= 114 Hz4)f
0=510 Hz . A comparer avec : (les valeurs sont très
voisines)
5) f
1= 120 Hz f2= 1800 Hz Df = 1600 Hz6)
7) f
1=618 Hz1/(2
pRC)=1/(2*p*250*1e-6)=630 Hz , valeur voisine de 620 HzDonc finalement , aux incertitudes près :f
1=1/(2pRC)8)
9)La courbe précédente permet d'affirmer , puisque U
S est constante au cours de l'expérience, que Us tend vers zéro lorsque la fréquence f augmente . Autrement dit , la tension efficace aux bornes d'un condensateur tend vers zéro lorsque la fréquence augmente . Cela revient à dire qu'un condensateur se comporte comme un court-circuit en haute fréquence .10)
En permutant R et C dans le circuit précédent , on obtient l'effet inverse , c'est à dire que T tend vers 0 lorsque f tend vers zéro : nous obtenons un filtre passe-haut .
11)
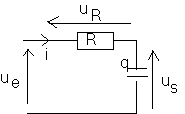
Nous pouvons écrire :
ou finalement :
12)u
e=f(t)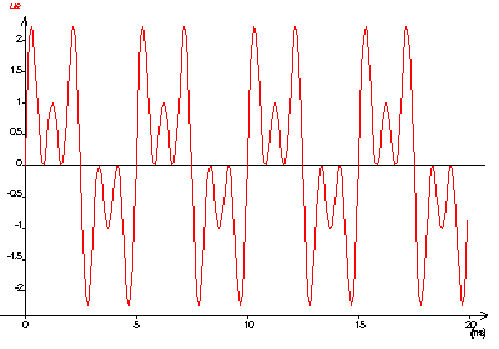
13)
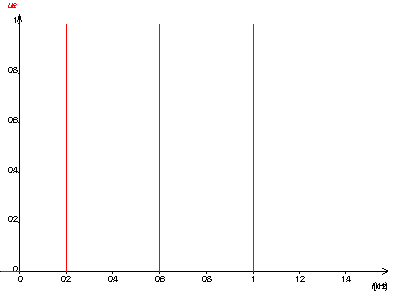
On retrouve les trois fréquences caractéristiques du signal d'entrée : 200 ; 600 et 1000 Hz . De plus le spectre met en évidence l'égalité des amplitudes des trois composantes du signal d'entrée .
14)
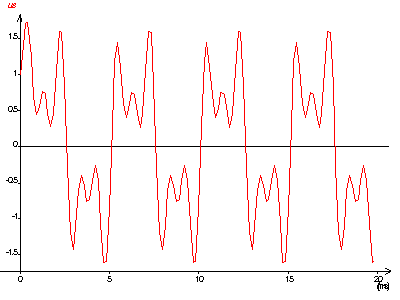
On remarquera facilement que u
s et ue ne sont pas identiques .15)
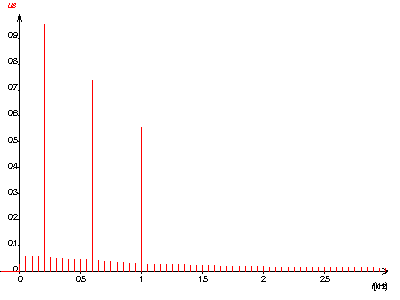
16)Les deux spectres sont différents . on note une atténuation lorsque la fréquence augmente , ce qui correspond bien à ce qui a déjà été observé à la question Q8 . Le filtre "ne laisse pas passer " les hautes fréquences : c'est un filtre passe-bas .