/ petanque.avi TP 9 : CHUTE VERTCALE DANS LE CHAMP DE PESANTEUR
I/Objectifs :
* Etudier la chute d'un objet en chute libre : boule de pétanque .
* Etudier la chute d'un objet dans le champ de pesanteur et soumis aux frottements de l'air : boule de polystyrène
* Méthode d'Euler ou méthode de résolution numérique d'une équation différentielle .
II/Chute libre verticale :
a)Exploitation de l'enregistrement vidéo :
L'enregistrement est celui d'une boule de pétanque abandonnée du deuxième étage d'un immeuble
A partir du dossier "REGRESSI" lancer "REGAVI" .
Lecture d'un fichier Avi
Ouverture d'un fichier image / petanque.avi
Agrandir la fenêtre au maximum 
. Si l'image
n'occupe pas tout l'écran , procéder à un rafraichissement (click 
).
Cliquer plusieurs fois sur 
et observer la
chute de la boule , puis revenir à la première image 
Mesures :
* 
Echelle
* Amener le curseur sur le bord inférieur de la fenêre du deuxième étage /click /Amener le cursur sur * le bord inférieur de la fenêtre du premier étage / Longueur en mètre : 3.20 /ok.
* Faire défiler quelques images de
façon à voir nettement la boule .
* Origine 
/Amener le curseur sur la boule et
cliquer
* 
Début des mesures
* Amener le curseur sur la boule (soyez précis) et cliquer et répéter l'opération jusqu'à ce que la boule soit pratiquement au sol .
* 
pour terminer les mesures/
pour transmettre les mesures à Regressi
* S'assurer que la case "Nouveau fichier" est cochée : 
b)Equation horaire y(t) :
Activer la "Fenêtre graphique" si elle ne l'est pas 
*
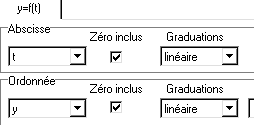
Coordonnées / ( t en abscisse , y en ordonnée)/Ok
*Click "Plus d'options" / Décocher "Axes orthonormés" /Ok
* 
Modéliser /
Modèle prédéfini /
Parabole /Ok /Ajuster .
Q1)Relevez sur votre copie :
* l'allure de la courbe .
* l'expression du modèle mathématique
* les valeurs de a, b et c données par Regressi .
* l'écart relatif
c)Vitesse Vy(t)
*Activer la fenêtre "Grandeurs" 
*
Créer grandeur
* Compléter la fenêtre comme indiqué ci-contre (Dérivée , vy , m/s, dy/dt)
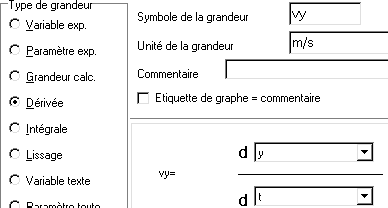
* Activer la fenêtre graphe
Faire apparaître à l'écran vy(t) et modéliser [ choisir le modèle "droite
" 
]
Q2)Relevez sur votre copie :
a) l'allure de la courbe vy(t);
b)l'expression du modèle mathématique ;
c) les valeurs de a et b données par Regressi ;
d) l'écart relatif
III/Chute verticale avec frottement :
a)Exploitation de l'enregistrement vidéo :
Avec la boule de polystyrène , les frottements ne sont plus négligeables
Comme précedemment , effectuer les mesures sur le fichier "ballepolyst.avi " .
Lorsque les pointages sont terminés :
*Stop / pour transmettre les mesures à
Regressi
* S'assurer que la case "Nouveau fichier" est cochée :
b) Exploitation des mesures :
Effectuer les mêmes étapes que pour la boule de pétanque sans modéliser
Q3)Représentez y(t) et vy(t) sur votre copie
Au cours de la chute la vitesse de la boule se stabilise : la vitesse limite est atteinte .
Q4)Quelle est la vitesse limite Vy,lim de la boule de polystyrène ?
IV/Méthode d'Euler :
a)Cas de la chute libre :
Le cas de la chute libre est assez simple à traiter mathématiquement .
L'équation différentielle du mouvement de la boule suivant l'axe vertical Oy s'écrit :
(Deuxième loi de Newton)
L'intégration de cette équation conduit à
et ce résultat est confirmé par l'expérience (voir II) .
b)Cas de la chute avec frottement
La boule de polysryrène est soumise à :
* son poids 
, soit en projection sur Oy : Py = mgy = -mg
* la poussée d'Archimède : 
( poids du volume V d'air déplacé par la boule de volume V) , soit en
projection sur l'axe Oy : py = -rVgy = rair Vg
* la résistance de l'air (en régime tourbillonnaire) : 
, soit en projection sur l'axe Oy : Ry = kvy2 . k est une constante qui dépend notamment de la forme de l'objet
D'après la deuxième loi de Newton : 
où 
est l'accélération du centre d'inertie de la boule . En projection
sur l'axe Oy , nous obtenons finalement :
Cette équation différentielle peut aussi s'écrire :
.
C'est une équation différentielle du second ordre et la forme analytique de sa solution est moins évidente que dans le cas de la chute libre .
Nous allons utiliser une méthode numérique pour déterminer la courbe y(t) : la méthode d'Euler .
c)la méthode d'Euler :
Reprenons les définitions approchées de l'accélération et de la vitesse :
et 
Ces définitions sont des définitions approchées de l'accélération et de la vitesse instantanée à l'instant tj , si l'intervalle de temps est petit . Modifions légèrement ces définitions :
et 
Ces expressions peuvent aussi s'écrire :
et
en posant Dt = tj+1-tj
Ces relations montrent que :
* si nous connaissons vy (à t=0) = vy,0 , y (à t=0) = y0 et ay(à t=0) =ay,0 , alors nous pouvons en déduire vy (à t=t1= Dt) = vy,1 et y (à t=t1=Dt) = y1 .
* Nous pouvons ensuite , par le même procédé , déterminer vy,2 et y2 à t=t2=2Dt , puis vy,3 , y3 etc.....
Si bien que finalement , nous pouvons construire la courbe de l'ensemble de points (tj, yj) . Nous avons ainsi réalisé une intégration numérique .
Nous comprenons que la méthode d'Euler donnera des résultats d'autant plus précis que le pas Dt sera "petit".
De l'équation différentielle précédemment écrite , nous déduisons :
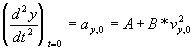
vy,0 et y0 sont accessibles à partir du
tableau de mesures de Regressi :Fenêtre "Grandeurs"/Variables
(ligne 0)
Nous montrerons (questions complémentaires) que A = - 9,5 ms-2 et B = 0,26 m-1
Nous allons charger le fichier de traitement avec Notepad (bloc notes de windows) et par un copier/coller nous allons l'incorporer à Regressi :
*Fichier/Nouveau/Notepad
*Fichier/ouvrir/C:\regwin\euler.txt
*Edition/selectionner tout
*Edition/copier
*Fichier/quitter
Dans Regressi : Activer la fenêtre "GRANDEURS"/Expressions
*placer le curseur de la souris en dessous de la dernière ligne
*Edition/coller
*
Mise à jour (si nécessaire)
Activer la fenêtre "GRAPHE"
Effectuer les opérations nécessaires pour visualiser dans la même fenêtre graphique :
* y(t) : courbe expérimentale
* ye(t) : courbe obtenue par intégration numérique de l'équation différentielle à partir des conditions initiales
Q5)Comparer les deux courbes . Conclure .
V/Questions complémentaires :
Q6)La chute de la boulle de pétanque permet t-elle de retrouver la valeur numérique du champ de pesanteur g = 9,8 m.s-2 . Justifiez votre réponse
Q7)Donnez un sens physique aux coefficients a,b et c calculés par Regressi dans II
Q8)Le rayon de la boule de polystyrène est égal à R=4 cm . Sa masse est égale à 11,6 g .
La masse volumique de l'air est égale à 1,3 g/L . g= 9,8 m/s2 . Retrouver la valeur de A précedemment annoncée .
Q9)Justifiez le fait que lorsque la vitesse limite Vlim est atteinte alors : A+B*v2lim=0 . En déduire la valeur de B . Calculer k .
TELECHARGEMENT DES FICHIERS RW3 ET EULER.TXT (compressés Zip)
TELECHARGEMENT DES FICHIERS AVI (nécessite l'installation du Codec Indeo® video 5)
TP P8 : Correction :
1)
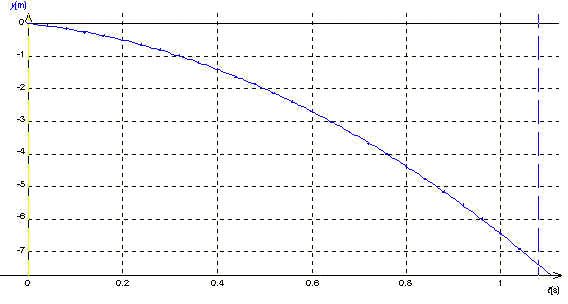
Modèle : y = ct2+bt+a
c = - 4,9 m.s-2
b = - 1,53 m.s-1
a = 0,004 m
écart relatif : 0,54 %
2)
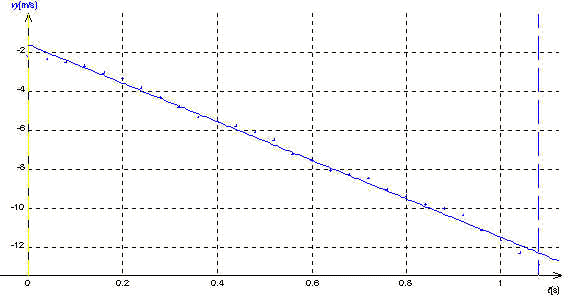
Modèle vy= at+b
a = - 9,8 m.s-2
b = -1,61 m.s-1
écart relatif : 3,2 %
3)
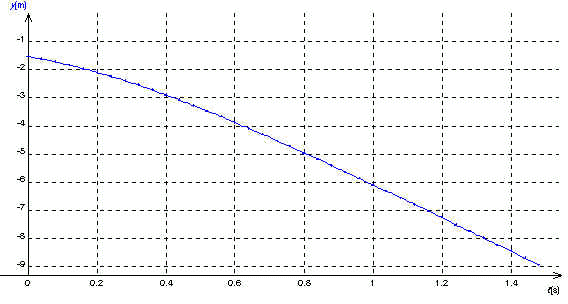
On remarque la partie linéaire de la courbe qui correspond à la phase où la balle a atteint sa vitesse limite (voir ci-après).
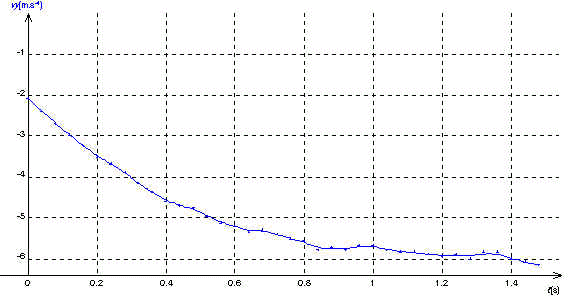
4)Vy,lim = -6 m/s
5)
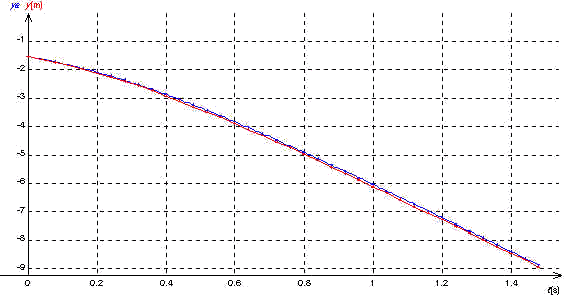
Il est clair que y(t) [courbe expérimentale] et ye(t) [courbe théorique obtenue par intégration numérique par la méthode d'Euler] sont pratiquement confondues .
6) Dans l'expression du modèle nous devons avoir ( voir IV a ) c=-g/2 = -9,8/2 = - 4,9 m/s2 : c'est effectivement ce que nous obtenons .
7)
*a est homogène à une distance (m) : c'est la "position" de la balle à t=0 (y(0)) dans le modèle donné par Regressi . On remarque que cette valeur est très proche de 0 . Cette valeur est notamment liée à la précision du premier pointage après avoir défini l'origine dans Regavi .
* b est homogène à une vitesse : c'est la vitesse de la balle à t=0
* c est homogène à une accélération (m.s-2) : voir question précédente .
8)
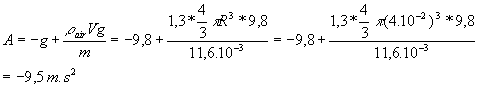
c'est ce qu'il fallait vérifier .
9)Lorsque la vitesse limite est atteinte vy = cte et donc d2y/dt = dvy/dt = 0 et l'équation différentielle peut alors s'écrire : A+B.(vy,lim)2 = 0 . D'où B= -A/(vy,lim)2 = 9,5 /36 = 0,26 m-1.
Or B=k/m et donc k = B*m = 0,26 * 11,6 10-3 = 3 10-3 kg.m-1 .