TP - ETUDE EXPERIMENTALE D'UNE BOBINE
Mesurer l'inductance L d'une bobine ,
Une tension en dents de scie est appliquée aux bornes d'un dipôle constitué par une résistance R et une bobine d'inductance L.
L'étude des oscillogrammes donnant uR = f(t) et uL = g(t) permet de déduire L connaissant R .
III/ Protocole expérimental :
1/Mesurer la résistance r de la bobine à l'ohmmètre.
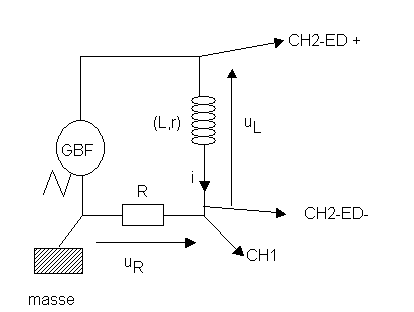
2/Réaliser le montage ci-dessous :
R est un conducteur ohmique de 10 kΩ
La bobine est utilisée sans noyau
Q1)Exprimer uR en fonction de R et i
Q2)Quelle est la tension observée en voie CH1 ?Q3)Quelle est la tension observée en voie CH2 ? (entrée différentielle)
Q4)Ecrivez l'expression de la tension instantanée uL aux bornes de la bobine en fonction de r, L et i. Que devient cette relation lorsque la résistance de la bobine peut être négligée ?Q5)Etablir la relation qui relie R, L, uL et lorsque r est négligée(Nous admettrons que les conditions expérimentales de l'expérience permettent de faire cette approximation) .
* signal délivré par le GBF de forme triangulaire
*fréquence : 500 Hz environ
4)Effectuer les réglages de l'oscilloscope :
* synchronisation voie CH1
* centrage des traces (ou réglage du zéro au milieu de l'écran )
* utilisation simultanée des deux voies ( voyant « ALT » ou "CHOP" allumé)
*calibrages (voies et base de temps adaptées aux signaux à observer ) : faire en sorte que l'oscillogramme occupe pratiquement tout l'écran sur environ deux périodes du signal )
*S'assurer que le voyant « TRIG » est bien allumé sinon le calibrage de la base de temps serait incorrect ).
IV/ Exploitation de l'oscillogramme :
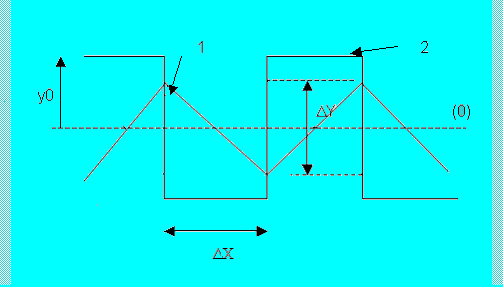
L'oscillogramme doit avoir l'allure ci-dessus
Q6)Représentez l'oscillogramme obtenu sur votre copie (soyez précis )et précisez à quelles voies correspondent les courbes (1) et (2)Q7)Quelles sont les valeurs :
1- du coefficient d'amplification de la voie CH1 : α1=.........?
2- du coefficient d'amplification de la voie CH2 : α2= ..... ?
3- de la sensibilité β de la base de temps ?
Utilisez les bonnes unités .
Q8)Mesurer en" div", y0, ΔX et ΔY et calculer u0 =α2 * y0 ,Δt=β*ΔX et ΔUR= α1* ΔY(ne pas oublier les unités)
Q9)Justifiez le fait que la courbe (2) est à une constante multiplicative près égale à la dérivée par rapport au temps de la courbe (1)
Q10)Monter que 
et
calculer L
Q11)Sur quelle voie l'intensité algébrique i est-elle visualisée indirectement ? Justifiez votre réponse.
2)En CH1 , on observe uR
3)En CH2 (entrée différentielle) on observe uL
4)
. Lorsque r est négligeable , cette
relation devient : 
5)En
utilisant la relation (1) , nous obtenons 
.
Autrement dit , à une constante multiplicative
près uL est
égale à la dérivée
de uL
par rapport au temps .
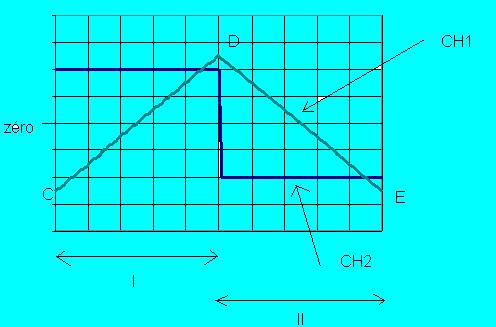
La courbe (1) ou uR , est visualisée en CH1 , la courbe (2) ou uL est visualisée en CH2
7)α1 = 2 V.div-1 ; α2 = 0,05 V.div-1 ; β= 0,2 ms.div-1 .
8)Sur l'oscillogramme ci-dessus :
y0= 2 div , ΔX = 5 div , ΔY= 4 div ; u0=0,05*2=0,1 V ; Δt=0,2*4=0,8 ms ; ΔUR=2*4=8 V
9)La relation établie à la question Q5 , revient bien à affirmer que uL est à une constante multiplicatives près (L/R) , la dérivée (par rapport au temps) de uR . Autrement dit , la tension observée en CH2 , qui correspond à la courbe (2) est égale à une constante multiplicative près à la tension observée en CH1 qui correspond à la courbe (1). La courbe (2) est donc bien à une constante multiplicative près, la dérivée de la courbe (1) par rapport au temps.
10)Considérons les deux courbes de l'oscillogramme sur la première partie de l'oscillogramme (zone I). La courbe (1) est une fonction affine qui peut par conséquent se mettre sous la forme uR= a*t + b .Il est clair dans ce cas que duR/dt= a=
(coefficient directeur) .
La courbe (2) est une constante u0 .
Finalement
, comme u0= 
,
nous en déduisons u0=
,
relation qui s'écrit aussi :
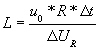c.q.f.d
Numériquement
: L=
11)i est visualisée indirectement sur CH1 car uR = Ri (Deux grandeurs proportionnelles ont la même "allure" ).