TP 11 : L'OSCILLATEUR MECANIQUE
I/Acquisition :
Elle est faite au bureau (poste professeur) .
*Matériel utilisé : banc magnum (soufflerie , règle ,ressorts , mobile) : voir le cours
*Paramètres : masse du mobile : m=50 g
constante de raideur du ressort équivalent à l'ensemble des deux ressorts : k=3,04 N.m-1.
*logiciel d'acquisition : OSCGTI . Ce logiciel permet de réaliser l'acquisition et fournit un fichier au format Regressi (extension rw3).
*logiciel de traitement : Regressi
Remarque : la constante de raideur du ressort équivalent est égale à la soome des constantes de raideur de chacun des deux ressorts .
On réalise deux acquisitions :
* la soufflerie est utilisée à pleine puissance : dans ce cas l'amortissement est négligeable
fichier d'acquisition : nonamorti.rw3
* la puissance de la soufflerie est réduite : l'amortissement n'est pas négligeable .
fichier d'acquisition : amorti.rw3
Q1)Proposez une méthode qui permette de déterminer simplement la constante de raideur d'un resort (on rappelle que la tension d'un ressort est proportionnelle à son allongement)
II/L'oscillateur non amorti :
A partir du dossier "Travaux Pratiques" sur le bureau de l'ordinateur, ouvrir le sous-dossier "Oscillateur mécanique" . Double-cliquer sur l'icône " Oscillateur non amorti " . Regressi est lancé et charge le fichier nonamorti.rw3
a)Période et amplitude :
A partir de la fenêtre Graphe de Regressi (l'activer si elle ne l'est pas) :![]()
*Curseur standart/réticule
Q2)Mesurer la période T0 de l'oscillateur en détaillant la méthode utilisée .T0 = ............
Q3)La relation ![]() est-elle vérifiée ?
est-elle vérifiée ?
Q4)Montrer que ![]() est homogène à un temps .
est homogène à un temps .
Q5)Mesurer l'amplitude des oscillations en détaillant la méthode utilisée . Xm = ................
*![]() Modéliser/
Modéliser/![]() Modèle prédéfini/
Modèle prédéfini/ sinusoïde pure/Ok
sinusoïde pure/Ok
*Ajuster
Le modèle proposé par Regressi est de la forme :x(t)=a+b*sin(2*pt/T+j)
Q6)Quelles sont les valeurs de a,b,T et j ?Comparer a et b et en déduire une expression simplifiée de x(t) . Comparer b et Xm , T et T0 .
Q7)Donner l'expression littérale de x à t=0 et la valeur numérique de x(0) . En déduire le valeur de j à partir de celle de x(0) . Comparer à la valeur de j donnée par Regressi (question précédente)
b)Energie :
![]() est l'énergie potentielle élastique
du mobile soumis à l'action du ressort de constante de raideur k ( lorsque le ressort est
dans sa position de repos x=0 , autrement dit x est égal à l'allongement ou à la
contraction du ressort )
est l'énergie potentielle élastique
du mobile soumis à l'action du ressort de constante de raideur k ( lorsque le ressort est
dans sa position de repos x=0 , autrement dit x est égal à l'allongement ou à la
contraction du ressort )
![]() est l'énergie cinétique de la masse m
lorsque sa vitesse est égale à V
est l'énergie cinétique de la masse m
lorsque sa vitesse est égale à V
![]() est l'énergie
potentielle de pesanteur de la masse m dans le champ de pesanteur
est l'énergie
potentielle de pesanteur de la masse m dans le champ de pesanteur ![]() . L'axe Oz est un axe ascendant dont l'origine est par exemple au
niveau de la table sur laquelle a été posé l'ensemble MAGNUM lorsqu'a été réalisée
l'acquisition .
. L'axe Oz est un axe ascendant dont l'origine est par exemple au
niveau de la table sur laquelle a été posé l'ensemble MAGNUM lorsqu'a été réalisée
l'acquisition .
![]() est l'énergie mécanique de la masse
m soumise à l'action du ressort et placée dans le champ de pesanteur
est l'énergie mécanique de la masse
m soumise à l'action du ressort et placée dans le champ de pesanteur ![]()
Q8)Que peut-on dire de l'énergie potentielle de pesanteur au cours de l'expérience ?
Par la suite , nous ne prendrons plus en compte l'énergie potentielle de pesanteur et nous appellerons Energie mécanique du système {ressort-masse} la grandeur :
![]()
*Activer la fenêtre GRANDEURS ![]()
*Activer l'onglet EXPRESSIONS s'il ne l'est pas
*Recopier dans la fenêtre les expressions (attention , Regressi distingue les minuscules des majuscules) :
v=DIFF(x,t)
Ec=0.5*0.05*v^2
Ep=0.5*3.04*x^2
E=Ep+Ec
Pour afficher x(t) dans la fenêtre graphique : (x et t étant déjà reconnues par Regressi)
*Coordonnées ![]()
*Compléter la fenêtre : 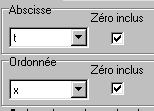 /Ok
/Ok
Pour Ajouter une courbe supplémentaire y(t) dans la fenêtre graphique :( y et t étant déjà reconnues par Regressi)
*Coordonnées ![]()
*Ajouter une courbe :![]()
*Compléter la fenêtre :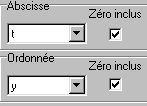 /Ok
/Ok
Pour choisir deux axes (l'un à gauche , l'autre à droite) indépendants
Choix de l'axe vertical à droite
*Coordonnées ![]()
* Sélectionner l'onglet correspondant à la courbe dont on veut que l'axe des ordonnées soit situé à droite
* dans la liste déroulante "echelle " choisir "à droite"  /Ok
/Ok
*Afficher dans la fenêtre graphique :x(t) , Ep(t) ,Ec(t) et E(t)
* Choisir l'axe correspondant à Ox à droite de l'écran
Q9)Comparer la période T0 de x(t) à celle des énergies Ep et Ec
Q10)Que peut-on dire des signes des différentes énergies ?
Q11)"Aux fluctuations près ", l'énergie mécanique est-elle conservée ?
Q12)Que peut-on dire des sens de variation de E
p et Ec ? Interprétez .Q13)Que peut-on dire de l'énergie potentielle lorsque l'énergie cinétique est nulle ? de l'énergie cinétique lorsque l'énergie potentielle est nulle ?
III/L'oscillateur amorti :
Fermer Regressi (Fichier/quitter ....... sans sauver!)
A partir du dossier "Travaux Pratiques" sur le bureau de l'ordinateur, ouvrir le sous-dossier "Oscillateur mécanique" . Double-cliquer sur l'icône " Oscillateur amorti " . Regressi est lancé et charge le fichier amorti.rw3
a)Pseudo-période :
Q14)Déterminer la pseudo-période T et comparer à T0 .
b)Energie :
Dans la fenêtre EXPRESSIONS , recopier les mêmes fonctions que dans II/-b
Visualiser dans la fenêtre graphique x(t) , Ep(t) ,Ec(t) et E(t) , l'axe de x étant à droite de l'écran .
Q15)Comparer la pseudo-période T de x(t) à celle des énergies Ep et Ec
Q16)Comparer E et E
p lorsque Ec est nulle . Comparer E et Ec lorsque Ep est nulle .Q17)L'énergie mécanique du système {masse-ressort} est-elle conservée au cours du temps ?
Q18)Interprétez la perte d'énergie mécanique du système .
TP 11 : correction
1)On mesure la longueur à vide du ressort L
0 . On suspend ensuite une masse m à ce ressort . La masse m au repos est soumise à deux forces : son poidsComme T=k(L
0-L) , nous en déduisons k= mg/(L0-L) .2)
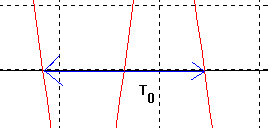
T
0 = 1230-415=815 ms = 0,8 s3)
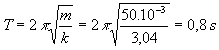
T=T
0 : la relation est donc vérifiée .4)
En remarquant que [F]=[m][a] ou N= kg.m.s
-2 , nous pouvons écrire : c.q.f.d
c.q.f.d
5) La courbe étant centrée , nous pouvons mesurer X
m directement :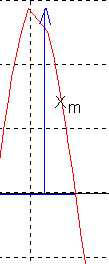
X
m= 29,5 mm
6) la modélisation avec Regressi donne :
a=-0,297 mm
b=29 mm
j
=-0,1 radT= 0,8 s
Nous avons ici a<< b et nous pouvons alors écrire
![]()
Nous obtenons donc b=X
m et T=T0 .7)x(0)= b.sin
jx(0) = -3,6 mm (valeur mesurée avec le curseur) d'où sin
j = -3,6/29= -0,12 ou j= - 0,12 rad , ce qui correspond pratiquement à la valeur calculée par Regressi au cours de la modélisation .8)L'oscillateur étant horizontal , l'énergie potentielle de pesanteur est constante au cours de l'expérience .
9)La période des énergies est égale à T
0/210)Les énergies sont positives
11)Aux fluctuations près l'énergie mécanique est pratiquement constante : elle est donc conservée .
12)E
p et Ec varient en sens inverse . Cela signifie que lorsque l'oscillateur perd de l'énergie potentielle il gagne de l'énergie cinétique : il y a donc échange entre les deux formes d'énergie , de façon à ce que leur somme soit constante (système conservatif)13)L'énergie potentielle est maximale lorsque l'énergie cinétique est nulle . L'énergie cinétique est maximale lorsque l'énergie potentielle est nulle .
14)T=0,79 s pratiquement égale à T
0 .15)La pseudo-période des énergies est égale à T/2
16)Lorsque E
c=0 , E= Ep . Lorsque Ep=0 , E=Ec .17)Il apparaît que E est une fonction décroissante du temps . E n'est donc pas conservée au cours du temps .
18)La perte d'énergie mécanique est due aux frottements .