Oscillateur mécanique :
Dans un plan horizontal, on considère un système oscillant formé d'un mobile autoporteur lié à deux points fixes par l'intermédiaire de deux ressorts élastiques identiques, de masses négligeables, et de même axe . Le système initialement au repos est écarté de sa position d'équilibre en déplaçant le centre d'inertie G du mobile le long de l'axe des deux ressorts . L'ensemble des deux ressorts est équivalent à un ressort de constante de raideur k = 15,4 N.m-1 .
On rappelle que :
* les notations ![]() représentent respectivement les dérivées première et seconde de y par rapport au temps
.
représentent respectivement les dérivées première et seconde de y par rapport au temps
.
* L'élongation y d'un oscillateur linéaire sans amortissement
satisfait à l'équation différentielle ![]() ,
dont les solutions y(t) sont sinusoidales de pulsation w
,
dont les solutions y(t) sont sinusoidales de pulsation w
Une table à numériser permet la détermination des positions
successives y de G dans un repère lié à la table ; la trajectoire de G est portée par
l'axe y'y. Un logiciel de traitement de données permet d'afficher les points
correspondant aux couples (t,y), (t,![]() ), ou
toute autre fonction souhaitée, et d'en représenter les courbes.
), ou
toute autre fonction souhaitée, et d'en représenter les courbes.
1- Première partie
Dans toute cette partie, le mobile a pour masse m=220 g et le système considéré est non amorti.
a) La figure 1 représente l'ensemble des points d'enregistrement (t,y). Ces points se situent sur une courbe d'allure sinusoïdale. Déterminer graphiquement la valeur de la période T et de l'élongation maximale Ym de y . A partir de la valeur de T , calculer la pulsation w de cet oscillateur .

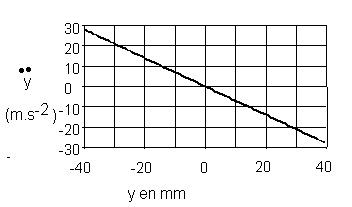 fig1 fig 2
fig1 fig 2
b)La figure 2 ci-dessus , représente les couples ![]() . Montrer que ce graphique est en accord avec
l'équation différentielle proposée . Que représente le coefficient directeur de la
droite support de cet ensemble de points ? Déterminer graphiquement sa valeur (attention
aux unités ) et en déduire l'ordre de grandeur de la pulsation w de l'oscillateur .
. Montrer que ce graphique est en accord avec
l'équation différentielle proposée . Que représente le coefficient directeur de la
droite support de cet ensemble de points ? Déterminer graphiquement sa valeur (attention
aux unités ) et en déduire l'ordre de grandeur de la pulsation w de l'oscillateur .
c)Les valeurs expérimentales de la pulsation déterminées en a/ et b/
sont-elles compatibles avec la valeur théorique de la pulsation propre w0 =
![]() de cet oscillateur ?
de cet oscillateur ?
d)Ecrire la relation de conservation de l'énergie E pour un
oscillateur se déplaçant en translation sans frottement . Montrer qu'elle peut s'écrire
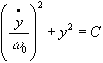 où C est une constante qui s'exprime en
fonction de k et de E .
où C est une constante qui s'exprime en
fonction de k et de E .
Exprimer C en fonction de Ym et calculer sa valeur
e)Pour traduire la conservation de l'énergie sur un graphe , on peut utiliser les représentations des couples :

Reporter sur votre feuille les deux représentations choisies parmi les trois proposées, en précisant les grandeurs portées sur les axes .

2- Deuxième partie
Les ressorts étant inchangés, un dispositif d'amortissement est désormais fixé sur le mobile . On réalise un nouvel enregistrement représenté sur la figure 3
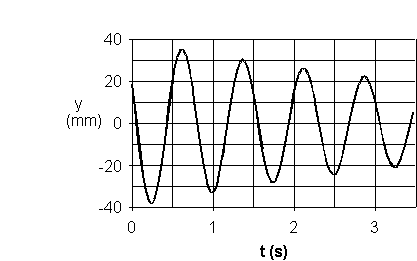
En utilisant deux valeurs consécutives de la valeur maximale de y, donner un ordre de grandeur du pourcentage de l'énergie perdue par l'oscillateur au cours d'une période .
Quelles sont les causes physiques de la dissipation ?
CORRECTION :
Première partie :
a)La durée entre deux maxima consécutifs correspond à une période T=0,75 s
L'amplitude est égale à l'élongation maximale autour de la position d'équilibre : l'enregistrement donne ym=40 mm . La pulsation est donnée par w= 2p/T=8,3 rd.s-1 .
b)L'équation différentielle ![]() s'écrit aussi
s'écrit aussi ![]() , autrement dit d2y/dt2 est une fonction linéaire de y , ce qui correspond bien à la figure 2 . le
coefficient directeur de la droite correspondante est négatif et égal à -w2 .
Soient les points A (yA=-30 mm et (d2y/dt2)A=2 m.s-2 et B (yB=-30 mm et (d2y/dt2)B= -2 m.s-2 ) de la droite . Le coefficient directeur est :
, autrement dit d2y/dt2 est une fonction linéaire de y , ce qui correspond bien à la figure 2 . le
coefficient directeur de la droite correspondante est négatif et égal à -w2 .
Soient les points A (yA=-30 mm et (d2y/dt2)A=2 m.s-2 et B (yB=-30 mm et (d2y/dt2)B= -2 m.s-2 ) de la droite . Le coefficient directeur est :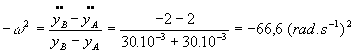
Nous en déduisons ![]()
c) ![]() . Cette valeur est
compatible avec les deux valeurs précedemment trouvées .
. Cette valeur est
compatible avec les deux valeurs précedemment trouvées .
d)Les oscillations ne sont pas amorties: le système est par conséquent conservatif et son énergie mécanique est constante .
![]() . Or
. Or ![]() et donc
et donc
 d'où nous déduisons
d'où nous déduisons ![]()
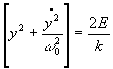 . C'est l'expression
cherchée en posant : C=2E/k.
. C'est l'expression
cherchée en posant : C=2E/k.
Or l'énergie est aussi égale à E=1/2kym2 (quand y=ym dy/dt=0) et par conséquent C=ym2
AN C= 1,6.10-3 m2 .
e)*Le système étant conservatif ,E= cste quelque soit t . Dans la représentation (t,E) cela correspond au graphe du milieu de l'énoncé .
*La relation 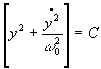 s'écrit aussi
s'écrit aussi  . Dans la représentation
. Dans la représentation 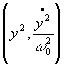 , cela correspond
au graphe de gauche (fonction affine à coefficient directeur négatif)
, cela correspond
au graphe de gauche (fonction affine à coefficient directeur négatif)
Deuxième partie:
Sur l'enregistrement , les deux premières valeurs consécutives de la valeur maximale de y sont y1,m=35 mm et y2,m =30 mm .
Quand y(t) est maximale , dyLdt est nulle et par conséquent E=1/2kym2 (énergie cinétique nulle)
E1=1/2 kym,12 = 9,4.10-3 J E2=1/2 kym,22 = 7.10-3 J
La variation relative d'énergie mécanique sur une durée correspondant à une pseudo-période est donc : (E1-E2)/E1 = 25 %
Remarque : Même pour un système non conservatif , nous pouvons toujours écrire E=Ep+Ec .