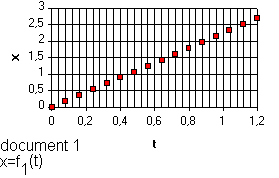
Mouvement d'une balle de tennis :
Documents :On étudie le mouvement d'une balle de tenis considérée comme un point matériel .
Ce mouvement est filmé avec un camescope dont l'axe de visée est perpendiculaire au plan de la trajectoire. Le fim est ensuite observé , image par image sur l'écran d'un téléviseur à l'aide d'un magnétoscope .
En s'aidant d'un quadrillage posé sur cet écran, on relève les coordonnées x et z de l'image de la balle . L'axe Ox est horizontal, l'axe Oz est vertical ascendant .La première image est prise à l'instant t=0, et on considère qu'à cette date les coordonnées x et z sont nulles . Le camescope enregistre 25 images par seconde, la date des autres images est alors connue.
Les valeurs de x,z et t sont entrés dans un fichier , puis traités par un logiciel adapté . Celui-ci permet de tracer les différents graphes figurant sur les documents ci-après
QUESTIONS
Sur les documents , toutes les valeurs numériques sont exprimées avec les unités du système international S.I. L'étude est faite dans le référentiel terrestre .
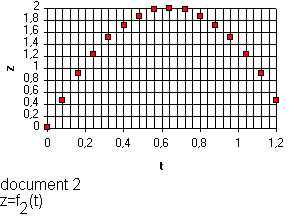
Les documents 1,2,3 et 4 représentent respectivement x=f
1(t) , z=f2(t) , z=f3(x) et vz=f4(t).1/Parmi ces quatres courbes, laquelle représente la trajectoire de la balle? Justifiez la réponse .
2/a-D'après le graphe x=f
1(t) quelle est la nature du mouvement de la projection de la balle sur l'axe Ox ?b-Calculer la valeur de la composante v
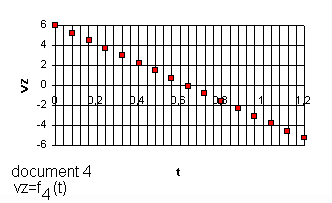
z du vecteur vitesse .3/Calculer la valeur de la composante v
z(0) du vecteur vitesse à la date t=0, en précisant le graphe utilisé .4/Calculer la valeur de l'angle
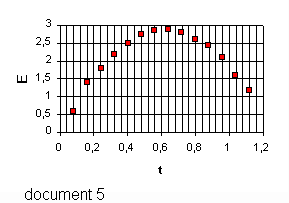
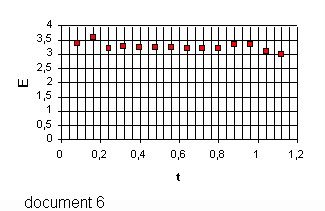
a de tir à t=0 .5/Les documents 5,6 et 7 représentent en fonction du temps les graphes de l'énergie cinétique , de l'énergie potentielle et de l'énergie mécanique de la balle dans le champ de pesanteur.
Identifier chaque graphe en justifiant la réponse sans faire de calculs .
6/a-Déterminer la date et la position de la balle pour lesquelles l'énergie cinétique du système est minimale .
b-A cette date , quelle est la valeur de chaque composante du vecteur vitesse ?


CORRECTION :
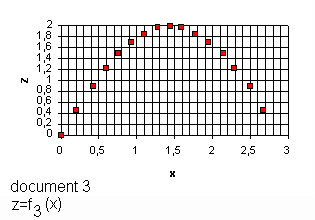
1/Le document 3 (z=f3(x)) représente la trajectoire de la balle . x et z sont des coordonnées d'espace , x suivant une direction horizontale , z suivant une direction verticale.
2/a- x=f1(t) est une fonction linéaire du temps : le mouvement projeté de la balle suivant cette direction est donc un mouvement uniforme .
b/vx = dx/dt =a car x=at et a est le coefficient directeur de la droite .vx=2,2 m/s
3/vz(0) peut être déterminée en utilisant le graphe du document 4 . vz(0) = 6 m/s
4/Nous utilisons le document 3 . Soit A le point de coordonnées xA=0,2 m et zA= 0,5 m. Ce point appartient à la tangente à z=f3(x) en O . L'angle de tir en O est tel que tg a = zA/xA , d'où a=68°
5/*document 5 : représente l'énergie potentielle Ep(t) avec Ep=mgz (référence prise au niveau du sol) . Ep(t) et z(t) ont donc la même allure
*document 7 : représente l'énergie cinétique Ec(t)=1/2 mv2=1/2 m(vx+vz)2 avec vz=vz,0-bt (document 4) où finalement , vx étant une constante :
Ec(t) = C+1/2 mb2t2-mvz,0bt (C: constante)
La forme analytique de Ec(t) correspond à celle du document 7.
*document 6 :représente l'énergie mécanique E=Ec+Ep
6/a-Ec(t) est minimale à t=0,64 s et nous avons alors x=1,4 m et z= 2 m (altitude maximale atteinte)
b-A t=0,64 s vx=dx/dt = 2,2 m/s ; vz=dz/dt = 0 m/s (document 4)