I/Objectifs :

* Connaître les trois lois de Kepler .
* Comparer les caractéristiques du vecteur accélération suivant que la trajectoire du centre d'inertie du satellite est un cercle ou une ellipse .

II/Les lois de Kepler :

A partir du Dossier "Travaux Pratiques" situé sur le bureau de l'ordinateur , ouvrir le dossier "Satellites" et lancer le fichier "Kepler" .

Utiliser cette documentation pour répondre aux questions suivantes :

Q1)Qui est Kepler ?

Q2)Enoncez la première loi de Kepler .Utilisez l'applet pour visualiser la trajectoire de Pluton autour du soleil . Le centre du soleil occupe un point particulier , caractéristique de l'ellipse :quel est le nom de ce point ?

Q3)Quelle est en mètres la valeur de l'unité astronomique (U.A ou A.U) ? Que représente cette distance ?

Q4)Enoncez la seconde loi de Kepler . Utilisez l'applet pour illustrer cette seconde loi . Faites  un schéma qui illustre cette  loi sur votre copie .

Q5)Enoncez la troisième loi de Kepler .L'applet qui illustre cette loi représente trois planètes en   mouvement autour du soleil : mercure , Vénus et la Terre . Quelles sont en jours les périodes de rotation de ces trois planètes autour du soleil ?

Q6)La période de rotation de la terre autour du soleil est égale à 365 jours et grand  axe de la trajectoire du centre de la terre autour du soleil est égal à 1 U.A.
En utilisant la troisième loi de Kepler, calculer en U.A. les grands axes de Mercure et de Vénus.

Q7)Les lois de Kepler s'appliquent-elles uniquement au mouvement des planètes ?

III/La trajectoire de Pluton :

a)La force gravitationnelle :

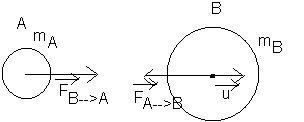
Etant données 2 deux m_A et m_B à symétrie sphérique (les masses sont sphériques et la masse volumique ne  dépend que de la distance du point considéré au centre de la sphère) : ces masses s'attirent réciproquement :

    

    

 

 

 : vecteur unitaire ; G = 6,67 10^-11 S.I.  : constante de gravitation universelle .

Les deux forces sont opposées (principe de l'action et de la réaction ou troisième loi de Newton)

b)Interaction Soleil-Pluton :

 

 

 

Le mouvement de Pluton sera étudié dans le plan Oxy , plan de sa trajectoire (voisin de l'écliptique) .

Pluton est uniquement soumise  à la force gravitationnelle :

              

D'après la deuxième loi de Newton , nous pouvons écrire : , d'où finalement :

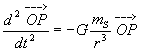                            avec r=OP = (distance soleil-Pluton) ,
x et y sont les coordonnées du vecteur .

Si nous projetons cette relation vectorielle sur les axes , nous obtenons :

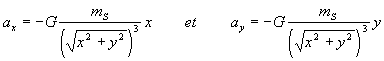
La valeur de G donnée plus haut est celle du système international . Si on exprime les distances en UA , les masses en kg , les accélérations en UA.jour^-2 , les vitesses en UA.jour^-1, on peut montrer que les deux relations écrites ci-dessus s'écrivent , sachant que m_S = 1,98 10³⁰ kg :

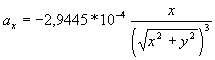     (1)   et  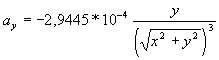           (2)

Ces expressions sont plus difficiles à gérer que celles obtenues lors de l'étude de la chute libre  ou d'une particule chargée dans un champ électrique. Pour cela , il est possible d'utiliser des méthodes numériques . Pour ce qui nous concerne , nous n'exploiterons pas ces équations ! Le fichier Regressi suivant nous permettra d'étudier quelques caractéristiques du mouvement de Pluton .

IV/Trajectoire elliptique et trajectoire circulaire :

a)Trajectoire elliptique de Pluton :

A partir du dossier "Satellites " , lancer le fichier "Pluton Regressi " . Ce fichier contient des données relatives au mouvement de Pluton .

Dans la fenêtre graphique de Regressi est représentée la trajectoire de Pluton avec les vecteurs vitesse et accélération .

Q8)Le mouvement de Pluton sur sa trajectoire est-il uniforme ? Justifiez votre réponse .

L'origine O du repère coïncide avec le centre du soleil :

Q9)Que peut-on dire de la direction du vecteur accélération à différents instants ? Comparez cette direction à celle de la force gravitationnelle . Cette observation est-elle cohérente avec la seconde loi de Newton ?.

Q10)La norme du vecteur accélération est-elle constante au cours du temps ?

b)Trajectoire circulaire :

Nous allons simuler un satellite dont le mouvement serait circulaire uniforme .

Sans quitter Regressi :

Fichier/Nouveau/simulation

Dans la fenêtre "EXPRESSIONS" écrire les deux relations suivantes :

x=40*cos(2*3.14*t)

y=40*sin(2*3.14*t)

puis Mise à jour

Activer la fenêtre GRAPHIQUE

Coordonnées

Activer l'onglet "Mecanique" si il ne l'est pas et cocher les cases :

            vitesse
            accélération
Axes orthonormés

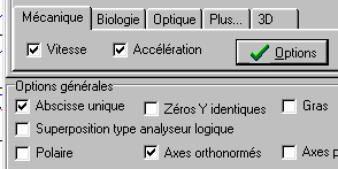
Ok

Q11)Commrent vérifier que le mouvement du satellite est bien uniforme ? Le vecteur vitesse   du satellite est-il constant ?Peut-on parler de mouvement circulaire uniforme ?

Q12)Que peut-on dire de la direction du vecteur accélération dans le cas d'un mouvement  circulaire uniforme du satellite ?

Q13)La norme du vecteur accélération est-elle constante dans le cas du mouvement circulaire   uniforme ?

V/Questions complémentaires :

Q14)Comment construire une ellipse avec deux pointes , un crayon et une ficelle .

Q15)Définir sur un schéma les différents éléments caractéristiques d'une ellipse :

            * foyers F et F'
            * grand axe
            * petit axe
            *centre de l'ellipse
            * distance c du centre au foyer
            *excentricité .

Q16)Un cercle peut -il être considéré comme un cas particulier de l'ellipse ? Quelle est son excentricité ?

VI/Exercices :

-travailler exercice résolu page 216

-chercher page 215 : 6,7 et 8  et page 219 : n°19

TP Satellites : correction

1)Johannes Kepler est un astronome allemand, qui établit que les orbites planétaires n'étaient pas circulaires, mais elliptiques. Kepler décrivait le mouvement des planètes à partir de trois lois.

2)première loi de Kepler :L'orbite de chaque planète est une ellipse et le Soleil occupe un foyer.Le soleil est au foyer de l'ellipse .

3)

1 UA = 1,49597870 · 10¹¹ m . L' UA est définie comme la distance moyenne entre la terre et le soleil

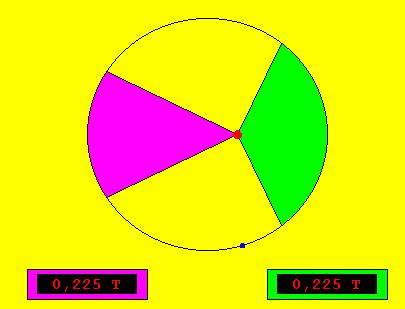
4)Seconde loi de Kepler :La ligne joignant la planète au soleil balaye des secteurs égaux dans des intervalles égaux de temps.

 

 

 

 

 

 

 

 

 

les aires balayées par le rayon vecteur pendant des intervalles de temps égaux  (ici 0,225 unités de temps ).sont égales .

5)Troisième loi de Kepler :Les carrés des périodes des planètes ( une période T représentant la durée d’une révolution complète autour du Soleil ) sont proportionnels aux cubes du demi grand axe de l'ellipse ( ou plus simplement du rayon r de la trajectoire si on néglige l'excentricité de l'orbite ). Plus une planète est loin du Soleil , plus elle met de temps pour parcourir son orbite.

 

T_Mercure = 88 jours

T_venus = 224 jours

T_terre = 365 jours

6)

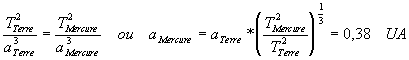
De la même manière , on trouve : a_Venus = 0,72 UA 

7)Les lois de Kepler peuvent être généralisées aux mouvements des satellites .

8)La norme du vecteur vitesse n'est pas constante : Pluton n'a donc pas un mouvement uniforme sur sa trajectoire .

9)Le vecteur accélèration est centripète : quel que soit la position de la planète , la direction du vecteur accélération passe par le foyer de l'ellipse (centre du soleil).

La force gravitationnelle exercée par le soleil sur Pluton a donc la même direction que le vecteur accélération , ce qui est tout à fait conforme à la seconde loi de Newton puisque  (la force gravitationnelle est la seule force extérieure appliquée à Pluton ).

10)Sur le graphique , on constate que la norme du vecteur accélération n'est pas constante .

11)Avec la trajectoire circulaire , la norme du vecteur vitesse est constante : il s'agit donc bien d'un mouvement circulaire uniforme .

12)L'accélération est centripète .

13)Dans le cas du mouvement circulaire uniforme , la norme du vecteur accélération est constante .

14)Pour construire l'ellipse , on fixe les deux pointes en F et F' auxquelles on attache les deux extrêmités de la ficelle . Avec le crayon , on maintient la ficelle tendue et nous pouvons ainsi tracer l'ellipse (l'ellipse est l'ensemble des points M telle que MF+MF'= constante ).

15)

                        

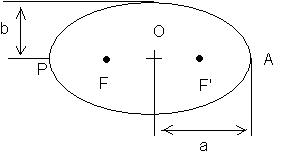
a: demi-grand axe

b: demi-petit axe

c = OF = OF' : demi-distance focale

e = c/a : excentricité de l'ellipse

De plus , on peut montrer que c² = a²  -  b²

^{16)Le cercle est une ellipse particulière d'excentricité nulle : e=c/a = 0/R = 0}

Satellites - correction des exercices :

Exercice 6 page 215:

a. La courbe ainsi obtenue est une ellipse : Tout point M de la courbe vérifie :P1M + P2M = cte (P₁ et P₂ sont les foyers de l'ellipse)

b. Mercure se situe sur la courbe (le point M par exemple) et le soleil doit se situer en P1 ou P2. En effet, d’après la 1e loi de Kepler ou loi des orbites, Mercure décrit, dans le référentiel héliocentrique, une ellipse dont le Soleil occupe l’un des foyers.

Exercice 7 page 215 :

a. D’après la 2e loi de Kepler ou loi des aires, le rayon [SP], qui relie le centre du Soleil à celui de la planète, balaie des aires égales pendant des durées égales : A = A’.

b. Pour respecter l’égalité précédente, P3P4 < P1P2. La distance parcourue pendant une même durée est plus grande lorsque la planète est plus loin du Soleil. Ainsi, la vitesse n’est pas la même entre P1 et P2 et entre P3 et P4.

P est plus rapide sur le trajet P1P2.

Exercice 8 page 215 :

a. En utilisant les valeurs données dans le tableau de l’exercice, nous avons :

Satellite	T2/r3 (jours2.km-3)	T2/r3 (s2.m-3)
Io	4,17.10-17	3,11.10-16
Europe	4,17.10-17	3,11.10-16
Ganymède	4,17.10-17	3,11.10-16
Callisto	4,17.10-17	3,11.10-16

la troisième loi de Képler T²/r³ = cste est vérifiée pour ces satellites

b) la cste dépend uniquement du centre attracteur , ici , plus exactement de la masse de Jupiter. A partir de ces données on peut donc calculer la masse de Jupiter.

Exercice 19 page 218 :

 a) La courbe T² = f(r³) est une droite passant par l’origine.  T² est proportionnel à r³. La 3eme loi de Kepler est vérifiée pour les satellites de la Terre : T² = k*r³  (k est une constante)

b)r_S = 24.10³ km  , d'où r_S³ = 1,4.10²² m³ . L'ordonnée du point d'abscisse 1,4.10²²  m³ étant T_S² = 1,4.10⁹ s² , nous en déduisons la période du satellite S : T_S = 3,7.10⁴ s.