I/Objectifs

- Suivre et comprendre par simulation avec Excel  l’expérience de déviation des électrons.

- Obtenir des graphes de trajectoires.

-Etudier l’influence des paramètres U_d : tension de déviation et U_a : tension accélératrice

-Déterminer l'équation de la trajectoire des électrons entre les plaques .

 

 

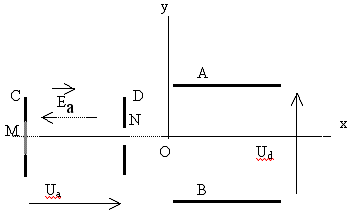
II/Description de l'’expérience.  (application : l'oscillographe cathodique)

Un faisceau d’électrons , émis par une cathode C , est accéléré par une tension V_D-V_C = U_DC = U_a =délivrée

par un générateur de haute tension .  

    

 

 

 

 

 

                                                                  

Le champ électrique     est uniforme .                                                                                                       

Le faisceau passe ensuite entre deux plaques

A et B, parallèles , distantes de  d = 40 mm                                                                                          

et soumises à la tension  U_AB = U_d .                                                                                        

L’utilisation de deux générateurs indépendants                                                          

permet d’observer expérimentalement l’influence  de chaque tension U_a et U_d sur la trajectoire des électrons.

III/Mouvement des électrons  :

a)Tension accélératrice

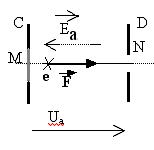
Q1)Reproduire le schéma des plaques C et D . Sur ce schéma représenter la force à laquelle est soumis un électron sur sa trajectoire MN .

Q2)Quelle est la nature du mouvement d'un électron entre M et N ?Justifiez clairement votre réponse .

Entre N et O on peut négliger le poids des électrons si bien que l'on peut considérer qu'ils ne sont soumis à aucune force  .

Q3)Que peut-on dire de la nature du mouvement d'un électron entre N et O ? Justifier clairement votre réponse .

Q4)Comparer la vitesse d'un électron en O à sa vitesse en N ?

Lorsque les électrons quittent la cathode, leur vitesse est pratiquement nulle .

On peut montrer que la vitesse d'un électron en O est donnée par la relation , où m est la masse d'un électron , e la valeur absolue de sa charge (appelée "charge élémentaire").

Q5)calculer V₀ lorsque la tension accélératrice est égale à U_a= 5000 V

b)Mouvement des électrons entre les plaques A et B

Q6)Représentez sur votre copie l'ensemble des plaques A et B ainsi que les axes Ox et Oy. Sur ce schéma représentez le champ électrique  dans l'hypothèse où la tension U_d serait positive .Complétez votre schéma en représentant la force à laquelle est soumis un électron entre les plaques A et B .   

Q7)Représentez le vecteur vitesse d'un électron en O.

Q8)Quelle est l'allure de la trajectoire d'un électron entre les plaques A et B ?

Q9)Déterminer les composantes du vecteur accélération dans le système d'axes Ox et Oy entre les plaques A et B en fonction de e , m , U_d et la distance d entre les plaques.

Q10)Déterminer en fonction du temps , les composantes du vecteur vitesse d'un électron entre les plaques A et B.

Q11)Montrer que les composantes du vecteur vitesse d'un électron lorsqu'il "sort" du champ électrique entre les plaques A et B (on appellera S le point de sortie)  sont :

                         

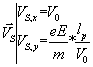
Q12)Déterminer l'équation de la trajectoire d'un électron entre les plaques A et B . En déduire que les coordonnées du point de sortie S sont :

                          

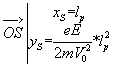
où l_p est la longueur des plaques A et B

c)Déviation :

Q13)A quelles forces est soumis un électron après le point S . Justifiez le fait que la trajectoire de l'électron est une droite entre S et l'écran

Nous pouvons écrire (voir schéma): 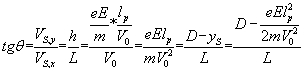 dont nous déduisons :

  ou  

Comme E =  , d étant la distance entre les plaques A et B , nous obtenons finalement :

                             

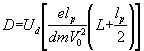
Pour une tension accélératrice donnée (autrement dit pour V₀ donnée) , l'expression entre crochets est une constante . Si nous posons 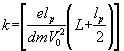 , nous obtenons D = k*U_d .  La déviation du faiseau d'électrons est donc proportionnelle à la tension appliquée entre les plaques A et B

                               

IV/Simulation :

Lancer "CHAMPE" à partir du dossier Microsoft

Le fichier est constitué de deux feuilles :

*Feuil1 : le tableau de calculs

*Feuil2 : la page graphique

a)Influence de U_d sur la déviation

Le curseur vertical permet de faire varier la tension de déviation entre - 3000 V et 3000 V.

Fixer avec le curseur horizontal la tension accélératrice à 8000 V.

Pour faire une mesure :

*Fixer U_d avec le curseur horizontal

*Cliquer sur le graphique (pour l'activer) : en déplaçant la souris sur le graphique , vous devez pouvoir lire les coordonnées x et y de la souris en bas de la page .

En cas de problème , il faut :

1-cliquer à l'extérieur du graphique

2-cliquer ensuite sur le graphique pour l'activer .

Q14)Effectuer une dizaines de mesures et tracer la courbe qui représente la déviation D sur l’écran en fonction de U_d . Conclure. Cela est-il conforme à ce qui a été vu ci-dessus ?

Q15)Justifiez le sens de déviation des électrons suivant que la tension U_d est négative ou positive .

b)Influence de U_a sur la déviation

Fixer la tension déviatrice à 1000 V

Faire varier la tension accélératrice entre 3000 et 8000 V

Q16) Quelle est l'influence de la tension accélératrice sur la déviation D .Comment peut-on justifier simplement ce résultat ?

V/Exercices

- voir exercice résolu 13 page 196

-chercher exercices 26 page 200 et 28 page 201.

TP correction : particule dans un champ électrique

1)L'électron est soumis à une force électrique avec q_e = - 1,6.10^-19 C . Comme q_e<0 la force électrique et le champ sont de sens contraires.

2)Un électron est soumis à son poids et à la force électrique , mais la masse de l'électron est suffisamment petite et la force électrique suffisamment grande pour que l'on puisse négliger le poids devant cette force électrique . Autrement dit, nous admettrons que l'électron est uniquement soumis à la force électrique et celle-ci est constante puisque le champ électrique est uniforme . D'après la seconde loi de Newton  où  est l'accélération de l'électron . Comme la force est constante , l'accélération  est constante .

Finalement , entre M et N , un électron a un mouvement rectiligne à accélération constante : il s'agit par conséquent d'un mouvement rectiligne uniformément varié .

3)Tout se passe entre N et O comme si l'électron n'était soumis à aucune force , autrement dit le "système électron" est isolé . En raison du principe d'inertie , un électron a un mouvement rectiligne uniforme .

4)Le mouvement d'un électron étant rectiligne uniforme , sa vitesse en N est la même qu'en 0 :

5)

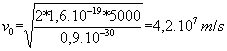
6)

Nous avons U_d=U_AB= . Les deux vecteurs ont la même direction . Comme le produit scalaire est positif (U_d >0) , ces deux vecteurs ont également le même sens , d'où la représentation de  sur le schéma ci-dessus .

Comme un électron est soumis à la force  , la force électrique à laquelle est soumis un électron est orientée de B vers A.

Nous sommes en fait dans un cas de figure analogue à celui d'une masse m dans un champ de pesanteur , le poids étant remplacé par la force électrique.

7)

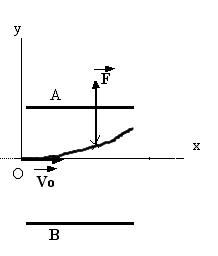
8)Entre les plaques A et B la trajectoire des électrons est une parabole .

9)Comme nous l'avons dit à la question 2) , nous négligeons le poids d'un électron devant la force électrique à laquelle il est soumis . Nous pouvons par conséquent écrire en appliquant la seconde loi de Newton :

                       où m est la masse d'un électron (m=0,9.10^-30 kg)

Comme de plus  , nous en déduisons  d'où 

Or les composantes de  dans le repère Oxy sont E_x = 0  et E_y = -E  (où E est ici , la norme du champ électrique).Les composantes de  dans ce même repère sont :

                    

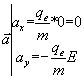
Sachant que U_d= , nous obtenons finalement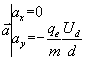

10)Nous savons que  , autrement dit , les composantes du vecteur vitesse  sont les primitives des composantes du vecteur accélération . Il s'en suit que :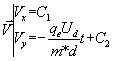 

Or à t=0 , les composantes de ce vecteur vitesse sont celles du vecteur vitesse  , ce qui implique C₁=V₀ et C₂ = 0 . Et donc , finalement , les composantes du vecteur vitesse , sont quel que soit l'instant t considéré :

                                        

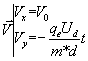
11)Les composantes du vecteur vitesse  que nous venons de déterminer à la question précédente montrent que le mouvement projeté d'un électron sur l'axe Ox est un mouvement rectiligne uniforme . Autrement dit , l'abscisse x_S du point de sortie est tel que x_S=V₀*t_S =l_p  (l_p est la longueur des plaques A et B), t_S étant le temps que met l'électron pour passer de O à S .

Sachant qu'en S 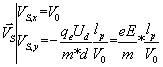  , nous obtenons finalement en remarquant que q_e=-e où e est la charge élémentaire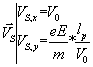   c.q.f.d.

12)L'intégration des composantes du vecteur vitesse en fonction de temps , nous permet de déterminer les composantes du vecteur déplacement :

                             

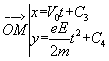
Sachant qu'à t=0 s , l'électron était en O de coordonnées (0,0) , nous en déduisons que nécessairement C₃=C₄ = 0, d'où quelque soit l'instant t considéré :

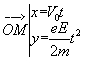                                , ce qui donne lorsque M est en S 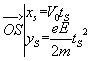 d'où en définitive , sachant que l_p=V₀*t_S=x_S  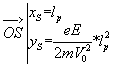:          c.q.f.d.

13)Entre S et l'écran les électrons ne sont soumis à aucune force (ils vont suffisamment vite pour ne pas "sentir" la pesanteur) : leur mouvement est donc un mouvement rectiligne uniforme en raison du principe d'inertie . Leur trajectoire entre S et l'écran est par conséquent une droite .

14)

Ud(V)	2489	2089	1689	989	389	0	-711	-1000	-1610
D (cm)	3,4	2,87	2,4	1,32	0,62	0	-0,97	-1,4	-2,17

Nous pouvons tracer la courbe correspondante D=f(U_d)

                       

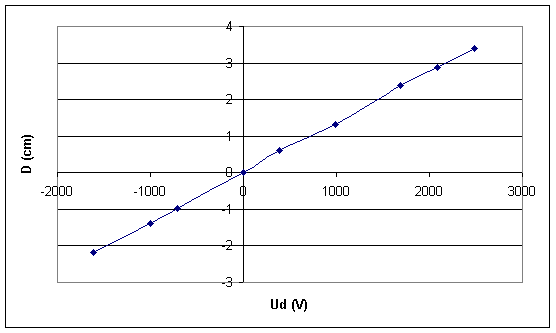
Nous observons bien que la déviation est proportionnelle à la tension U_d .

15)Quand U_d >0 , le champ électrique est orienté "vers le bas" , la force électrique est donc orientée vers le haut et la déviation se fait par conséquent vers le haut.

Quand U_d<0 , la force électrique est orientée vers le bas et la déviation se fait dans le même sens .

16)Plus la tension accélératrice U_a est élevée ,plus la déviation D est faible . D'après ce qui a été vu  ci-dessus , nous voyons que V₀ augmente avec U_a ( ) .Par ailleurs , quand V₀ augmente D diminue () .

Exercice 26 page 200

1/Le système que l’on étudie est l’électron entre les plaques P₁ et P₂.

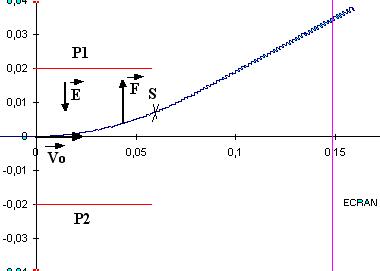
*les électrons sont déviés vers la plaque P₁ . Ils sont par conséquent soumis à une force dirigée vers le haut comme indiqué sur le schéma ci-dessus. Or cette force résulte du fait que l'électron de charge q_e =-e=-1,6.10^-19 C est dans le champ électrique . Comme  avec q_e<0 , il s'en suit que  sont colinéaires et de sens contraires (voir schéma)

* La force électrique est la seule force à laquelle un électron est soumis (le poids est négligeable devant cette force) et donc en raison de la deuxième loi de Newton (appliquée dans le repère terrestre galiléen (O,x,y) ) , nous pouvons écrire :

 d'où

*comme E_x=0 et E_y=-E  avec  , nous en déduisons a_x=0  et a_y= eE/m (attention aux signes)

2/a. Pour établir l’équation de la trajectoire, on établit dans un premier temps les coordonnées

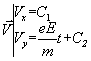du vecteur vitesse qui est le vecteur primitive par rapport au temps du vecteur accélération (car  ). Nous obtenons :  où C₁ et C₂ sont des constantes (constantes d'intégration).

Or à t=0 . Il en découle que nécessairement C₁=V₀ et C₂=0 . D'où finalement , quel que soit l'instant t considéré :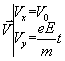

Comme 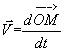 , le vecteur déplacement est une primitive du vecteur vitesse . En prenant en compte le fait qu'à t=0 , M est en O (origine des axes) , vous obtenons finalement :. L'équation de la trajectoire est obtenue en "reportant" t de la première coordonnée dans la seconde et nous obtenons :

  c.q.f.d.

b.La trajectoire est une parabole .

c.y_S est l'ordonnée du point de sortie du champ . L'abscisse de S est x_S = l (longueur des plaques) et donc y_S= [eE/(2mV₀²) ] l² = [eU/(2dmV₀²)]l² = [e/(2dmV₀²)]l² * U (sachant que E=U/d - voir TP), ce qui est bien de la forme y_S=kU

3.a : y_A= [e/(2dmV₀²)]l² * U * 2L/l = [eLl/(dmV₀²)] * U . La déviation est donc proportionnelle à la tension appliquée entre les plaques P₁ et P₂ .

b.Si on diminue U sans changer de signe , le spot(point d'impact A) descend tout en restant dans la moitié supérieure de l'écran .

Si U change de signe , l'ordonnée du spot devient négative (y_A<0)

Exercice 28 page 201

a)

Pour déterminer le sens du vecteur champ électrique il suffit de considérer une charge test positive (voir TP) . Ici  avec q=e>0 .

b.p = mg soit p = 4,8 × 10^-26 × 9,8 = 4,7 × 10^-25 N

f_e = 1,6 × 10^-19 × 1,0 × 10² = 1,6 × 10^-17 N

Il est clair que f_e >>p

c.Si était la seule force appliquée , nous pourrions écrire , en utilisant la seconde loi de Newton (le vecteur accélération a donc ici le direction et le sens du champ électrique )et donc en projetant sur l'axe Oz : qE_z=ma_{z .} Comme a_z=dv_z/dt , v_z est une primitive  de a_z et par conséquent (en remarquant ici que E_z=E) v_z = (eE/m)t+C . La vitesse v_Z étant nulle à t=0 , la constante C est donc nécessairement nulle , autrement dit v_z est une fonction linéaire du temps

 D'où la représentation ci-dessous . Il est clair que cette courbe ne correspond pas à l'évolution réelle de la vitesse.

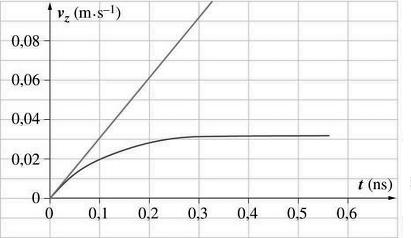
Il est clair que la particule n'est pas soumise qu'à la force électrique considérée mais également à d'autres forces non négligeables .

d.La vitesse limite étant constante , cela signifie que l'accélération est nulle , donc la somme vectorielle des forces extérieures appliquées à la particule est nulle :  où représente l'ensemble des autres forces appliquées à la particule. On peut penser que ces forces sont dues à d'autres ions présents dans l'atmosphère .