I/Objectifs :

* Etudier les paramètres du mouvement du centre d'inertie d'une balle lancée dans le champ de pesanteur avec une vitesse initiale.

* s'intéresser à la nature des "mouvements projetés" de la balle .

II/Acquisition :

A partir du dossier "REGRESSI" lancer "REGAVI" .

Lecture d'un fichier Avi

Ouverture d'un fichier image  / chutpar.avi

Agrandir la fenêtre au maximum  . Si l'image n'occupe pas tout l'écran , procéder à un rafraichissement (click  ).

Cliquer plusieurs fois sur  et observer la chute de la boule , puis revenir à la première image

Mesures :

* Echelle

* Amener le curseur sur le  trait supérieur de la règle (il n'est pas très visible !) /click /Amener le curesur sur  le trait inférieur de la règle /click / Longueur en mètre : 1 /ok.

* Faire défiler quelques images  de façon à voir nettement la balle .

* Origine /Amener le curseur sur la balle et cliquer

* Début des mesures

* Amener le curseur sur la balle (soyez précis) et cliquer . Répéter l'opération jusqu'à ce que la balle soit pratiquement au sol .

*  pour terminer les mesures/ pour transmettre les mesures à Regressi

* S'assurer que la case "Nouveau fichier" est cochée :

Ok

III/Equation de la trajectoire :

*Activer le fenêtre "GRAPHE "  si elle ne l'est pas

*click  ("Coordonnées")/décocher la case "Axes Orthonormés

*cocher l'option "ligne" si elle ne l'est pas  

*Ok

*Début Modélisation /Modèle prédéfini /Parabole /Ok

*Ajuster

            Q1)Ecrire sur votre copie l'expression de l'équation de la trajectoire et donnez les valeurs des             coefficients a,b et c calculés par Regressi .

*Curseur standart/Réticule

            Q2)Quelle est l'altitude maximale Y_F atteinte par le balle ou flèche ?Quelle est la valeur             numérique de l'abscisse X_F correspondante ?

            Q3)Quelle est  l'abscisse X_D du point D de la courbe (autre que l'origine) pour lequel Y_D = 0 ?

            Cette distance est appelée "portée"

IV/Etude des "mouvements projetés" du centre d'inertie de la balle :

a)notion de mouvement projeté :

Etant donné un point M de la trajectoire de coordonnées X_M et Y_M , soit  M_X un point de l'axe Ox tel que = X_M , et M_Y un point de l'axe OY tel que , les mouvements de M_X et M_Y sont les mouvements projetés de M .

b)Equation horaire de M_X ou x(t) :

*Fermer la fenêtre de modélisation (cliquer sur l'icône correspondante)

*click  ("Coordonnées")

*changer les paramètres de façon à visualiser x(t) /Ok

*Modéliser en choisissant le modèle linéaire (droite):/Remplacer modèle/ Ajuster

            Q4)Ecrire sur votre copie l'expression de l'équation de l'équation horaire x(t)  et donnez les             valeurs des   coefficients a et b  calculés par Regressi

c)Equation horaire de M_Y ou y(t)

Procéder comme précedemment (y(t) - modélisation) , mais en choisissant le modèle parabolique :

            Q5)Ecrire sur votre copie l'expression de l'équation de l'équation horaire y(t)  et donnez les             valeurs des   coefficients a , b et c  calculés par Regressi .

d)Vitesse de M_Y  ou v_Y(t)

*Activer la fenêtre "Grandeurs"

*Créer grandeur

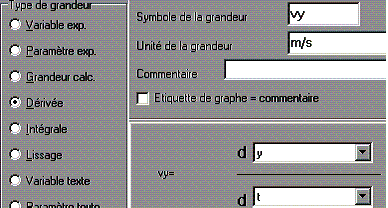
* Compléter la fenêtre comme indiqué ci-contre (Dérivée , vy , m/s, dy/dt)

* Activer la fenêtre graphe

*Activer la fenêtre graphique

*Visualiser vy(t) [voir précédemment]

*Modéliser

            Q6)Ecrire sur votre copie l'expression de l'équation de l'équation vy(t)  et donnez les     valeurs             des coefficients a et b   calculés par Regressi .

e) vx (t)

On pourra créer vx et visualiser vx(t) et vérifier qu'aux erreurs de pointage près vx(t) est pratiquement constante .

f)Conclusion :

* M_X a un mouvement uniforme car sa vitesse est constante ou x(t) est une fonction affine du temps

* M_Y a un mouvement uniformément varié car sa vitesse est une fonction affine du temps

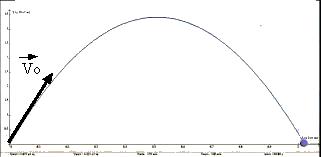
V/Bien viser !

Ouvrir le dossier Logiciel et lancer le logiciel "MOVE" .

            Q7)Lancez le boulet pour qu'il atteigne la cible  . Notez les valeurs de a et V₀ .

VI/Etude théorique :

            Q8)Donner une définition de la chute libre

1/Mise en équation :

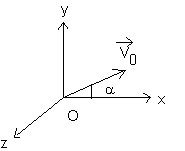
Le repère Oxy est un repère terrestre . Une masse ponctuelle m est lancée du point O à t=0 avec une vitesse initiale . On néglige les frottement de l'air .

Le vecteur vitesse   est dans le plan Oxy et fait un angle a avec l'axe Ox .

La durée de chute de la masse m étant relativement courte , le repère terrestre utilisé peut être considéré comme étant galiléen . Il est donc possible d'appliquer le théorème du centre d'inertie (ou deuxième loi de Newton) à la masse m dans ce repère .

            Q9)Représentez sur un schéma (sans faire de calculs) l'allure de la trajectoire de la masse     m.

            Q10)Soit M un point de la trajectoire . Effectuer le bilan des forces appliquées à la masse m   en M lorsque celle-ci est en chute libre. Représenter ces forces .

            Q11)Ecrire le théorème du centre d'inertie ou deuxième loi de Newton. En déduire les             composantes du vecteur    accélération de la masse m à un instant quelconque.

Par intégrations successives , nous allons en déduire , les composantes du vecteur vitesse à un instant t quelconque et l'équation de la trajectoire .

Comme     et que 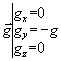 , nous pouvons écrire les composantes de 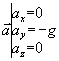  , ce qui s'écrit aussi  :               

Ce sont les équations différentielles du mouvement de M (g est la norme du vecteur de champ de pesanteur )

 *   : la composante du vecteur accélération suivant Oz est nulle .

Reprenant cette égalité  , une première intégration (primitive)conduit à   (C₁ est une constante).

Or à t=0 , la composante de  suivant Oz , est  V_0,z =0 , puisque le vecteur vitesse  est dans le plan Oxy . Comme v_z est constante quelle que soit l'instant t, cette constante ne peut qu'être égale à la valeur de v_z à t=0 , autrement dit C₁=0  : quel que soit t .

Une nouvelle intégration conduit à : z= C₂  quel que soit l'instant considéré.Un raisonnement analogue au précédent permet de conclure que C₂=0 puisque z=0 à t=0 (particule en O à t=0)

Finalement z=0  quel que soit t : quelque soit l'instant considéré , la particule est donc dans le plan Oxy .

 *

Une première intégration de ces deux équations conduit à :

   et     quel que soit t

A t=0  v_x(0)=v_0,x = v₀ cos a        et      v_y(0) = v_0,y = v₀ sin a

Cela signifie que lorsque nous remplaçons t par 0 , dans les deux expressions établies à la question précédente , nous devons obtenir respectivement v_0,x et v_0,y . Cela n'est possible que si :

         C₃= v₀ cos a  et   C₄ = v₀ sin a

Finalement :

         v_x = v₀ cos a        et   v_y = -gt + v₀ sin a     quel que soit t

* En poursuivant l'intégration , nous obtenons , quel que soit l'instant t considéré :

        x = (v₀ cos a) * t + C₅

           y = - 1/2 g t² + (V₀ sin a)*t + C₆ .

Comme à t = 0 , M est en O , c.à.d . x(0) = 0 et y(0) = 0 , nécessairement , les constantes C₅ et C₆ sont nulles .

D'où :x = (v₀ cos a) * t    et      y = - 1/2 g t² + (V₀ sin a)*t

*En éliminant t , nous pouvons à présent en déduire l'équation de la trajectoire .De la première égalité , nous déduisons t= x/(v₀ cos a) , et en reportant dans la seconde , nous obtenons :

                   

C'est l'équation de la trajectoire (parabole)

VII/Exercices :

Pages 198 et suiv:16, 19, 29 et 30

TP Particule dans le champ de pesanteur  - Correction :

1)y(x) = c x² + bx + c

c= -2,5 m^-1 ;  b = 1,7  et c=0,005 m

C'est l'équation d'une parabole . Aux erreurs de pointage près , la valeur de a est pratiquement nulle .

2) x_F= 35 cm ;  y_F =   29,6  cm .

x_F se calcule en écrivant que y(x) est extrêmale en F et par conséquent dy/dx= 0 . On reporte ensuite x_F dans l'équation y(x) pour en déduire y_F .

Remarque : Nous avons aussi en F dy/dx = v_y =0 : composante verticale du vecteur vitesse nulle .

3) x_D = 69,4cm  ;  y_D= 0

On calcule x_D en résolvant l'équation y(x)=0 . Une solution correspond à x_D .

4) x(t) = at + b

a= 1,44 m.s^-1

b= 0,007 m  : valeur pratiquement nulle aux erreurs de pointage près .

5)y(t) = ct² +bt+a

c= -5,04 m.s^-2  ; b= 2,4 m/s  et  a= 0,008 m (valeur pratiquement nulle aux erreurs de pointage près) .

Cette équation ne doit absolument pas être confondue avec y(x) [trajectoire] . y(t) est l'équation horaire du mouvement projeté de M sur l'axe Oy .

6)vy(t) = at+b

a = -9,9 m.s^-2  b=  2,4 m.s^-1 .

Cette expression de la vitesse est caractéristique d'un mouvement uniformément varié (mouvement projeté de M sur Oy) .

7)La simulation permet de constater que pour une cible donnée , il existe plusieurs couples (v₀,a) qui permettent d'atteindre la cible .

Exemples  :v₀=80 m/s  et  a= 30 °  ou    v₀= 85 m/s   et  a= 60°

8)Un corps est en chute libre s'il n'est soumis qu'à une seule force : son poids .

9)La trajectoire du centre d'inertie de la masse m est une parabole :

10)

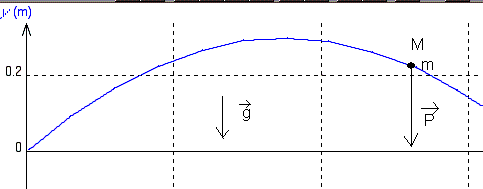
11)

 ( : deuxième loi de Newton .  : accélération du centre d'inertie) .

Comme de plus  , nous en déduisons .

Correction des exercices : Tp pesanteur

Exercice 16 page 198

a et b.

On distingue 3 zones :

 

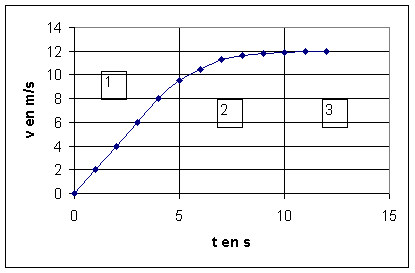
Dans la partie (1) entre 0s et 5 s, v est une fonction linéaire de t. Dans la partie (2) entre 5 s et 10 s, v est une fonction croissante du temps et dans la partie (3) entre 10 s et 13 s, v est une fonction constante (mouvement uniforme)

c)Dans la partie (1), l’accélération est a=dv/dt =coefficient directeur de la droite = 10/5 = 2 m/s2

Le mouvement est rectiligne uniformément accéléré.

d)Dans la partie (3), la vitesse étant constante , l'accélération est donc nulle.

e)À l’instant de date t = 7 s, on calcule l’accélération moyenne entre les dates 6 et 8 s soit :

a₇ = (v(t₈)-v(t₆))/(t₈-t₆) = (11,6-10,5)/2 =0,55 m.s^-2

Exercice 19 page 198 :

*À partir de t = 1 s, la valeur de la vitesse est constante (courbe 2). La chute étant verticale , la trajectoire est une droite .Le mouvement est donc rectiligne  et uniforme : l'affirmation est donc exacte .

*Après t = 1,5 s, l’ordonnée z continue à augmenter : la bille continue donc à descendre, elle n’a donc pas encore atteint le fond de l’éprouvette : l'affirmation est fausse.

*De t = 0 à t = 0,75 s, le mouvement ne peut pas être décéléré puisque la valeur absolue de la vitesse |vz| augmente : affirmation fausse.

Exercice 29 page 201 :

a)La balle est en chute libre puisqu'elle n'est soumise qu'à son poids . Par conséquent , en appliquant la seconde loi de Newton : d'où :

 et donc : a_x=0 m/s²  et a_z= -g

b)Équation de la trajectoire : à partir des coordonnées de l’accélération, par intégration, on obtient successivement les coordonnées du vecteur vitesse de la balle et les coordonnées du vecteur position :

v_x = v₀    v_z = -g × t

x = v₀ × t         z = - ½ g × t² + H

En éliminant t entre x(t) et z(t), on obtient :

c)Pour que la balle passe au-dessus du filet, il faut que lorsque x = x_filet=12 m  on ait z_filet > h .

Or 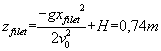 . La balle rentre donc dans le filet .

Exercice 30 page 201 :

a)Coordonnées du vecteur vitesse à t₀ = 0s sont v_0x = v₀cosα  v_0z = v₀sinα

b)Le système étudié est la balle. Le référentiel choisi est le référentiel terrestre galiléen.

La balle est soumise à une seule force, son poids. En appliquant la deuxième loi de Newton pour un solide de masse m constante on obtient : , d'où dans le repère considéré : a_x= 0 m/s² , a_z= -g

c)Par intégration, on obtient les coordonnées du vecteur vitesse :

v_x = C₁ = v₀cosα        et  v_z = -gt + C₂          avec ici C₂ = v₀sinα

d)En intégrant à nouveau , nous en déduisons on établit les coordonnées du vecteur position , en sachant qu'à t₀= 0 s nous devons avoir x=0 m  et  z= 0 m :   x = (v₀cosα)t  et  z = -1/2 gt² + (v₀ sinα)t

e)La vitesse en S n'est pas nulle. Quelle que soit la position de la balle, elle garde une même vitesse de déplacement horizontale v_x = v₀ cosα.

f)En S , la composante verticale de la vitesse est nulle v_S,z= 0 m/s  d'où -gt_S+ v₀ sina=0  et donc t_s=(v₀ sin a)/g . En reportant t_S dans z(t) , nous obtenons :

z_S = -1/2 g[(v₀ sin a)/g]² + (v₀ sinα)*(v₀ sin a)/g = (v₀² sin² a)/2g

g)La portée correspond à z=0 . Or en combinant les deux égalités établies dans d) nous obtenons :

                 z= - 1/2 g * x²/(v₀²*cos² a) + tg a * x

Pour z= 0 , nous obtenons  x*[-1/2g*x/(v₀²cos² a)+(sin a / cos a)].

La solution x=0 ne convient pas (point de départ) . Nous obtenons donc finalement :

             x_I = (2 v₀² cos²a *sin a /g cos a)= 2 v₀² sin a cos a/g = (v₀² sin 2a)/g

h)En remplaçant par les valeurs numériques proposées nous obtenons : z_S = 4,1 m      et   x_I = 29 m