Correction des exercices "principes de la mécanique"

Eercice 3 page 174:

Un objet tombe dans un train en mouvement.

Dans le référentiel du train, la trajectoire de son centre d’inertie est une droite verticale.

Dans le référentiel terrestre, la trajectoire est une courbe, combinaison du mouvement de chute et du mouvement du train.

Exercice 4 page 174:

 a. À t₀ = 0 s, x(t₀) = 1 et y(t₀) = 3.

Le vecteur position est par définition :                   

b. Le vecteur vitesse est la dérivée du vecteur position par rapport au temps :

c. Le vecteur vitesse est un vecteur constant, la trajectoire est une droite et le mouvement est rectiligne uniforme.

Exercice 5 page 175:

a. Le vecteur vitesse est la dérivée du vecteur position par rapport au temps.

b. L’expression approchée du vecteur vitesse étant :

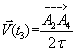
Le vecteur vitesse à la date t₃ a même direction et même sens que le vecteur    .

 Sa valeur est donnée par : V₃=A₂A₄/2t

Pour tout le quadrillage : 13 carreaux correspondent à  13 cm dans la réalité et mesurent 7,0 cm

sur le papier.

A₂A₄ a une mesure de 2,4 cm sur le papier.  Les grandeurs réelles  son proportionnelles aux grandeurs sur le papier: cela signifie que A₂A₄ dans la réalité et 13 cm sont respectivement proportionnels à A₂A₄ sur le papier (2,4 cm) et  à 7 cm. Par conséquent:

  ou A₂A₄ réalité = 13*2,4/7 = 4,5 cm

Finalement V₃= (4,5.10^-2)/(2*40.10^-3)=0,56 m/s.

Exercice 6 page 175:

a. Le tracé correspondant au centre d’inertie du mobile est celui du traceur « B ».

b. Le tracé correspondant au centre d’inertie est formé de points alignés et régulièrement

répartis : le mouvement du centre d’inertie est rectiligne uniforme. D’après le principe d’inertie, le système étudié

dans un référentiel considéré comme galiléen est alors un système isolé si :

                 

c. Le mobile autoporteur est en interaction avec la Terre, le coussin d’air et l’air ambiant d’où le diagramme suivant :

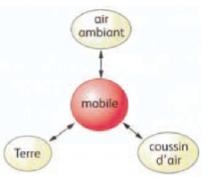
L’action due à la Terre est modélisée par le poids , l’action du coussin d’air par une force . En négligeant l’action de l’air ambiant :  soit

Exercice 7 page 175:

7. a. Le vecteur quantité de mouvement d’un point matériel de masse m et animé d’une vitesse  est :

Le vecteur quantité de mouvement d’un système matériel est égale à la somme des vecteurs quantités de mouvement des n points matériels qui le constituent :                          .

b.  p = mv = 1.10³ * =3,3.10⁴ kg.m.s^-1 .

c. On note M, la masse du camion et V, sa vitesse.

 p = mv = MV ; d’où V=(m/M)*v = 120/30= 4 km.h^-1 .

Exercice 8 page 175:

a. Dans le référentiel terrestre considéré comme galiléen, on étudie le système constitué par les deux patineurs.

b. Avant qu’ils ne se repoussent, les patineurs sont immobiles, leur quantité de mouvement est nulle. La quantité de mouvement du système est alors nulle :

Lorsque A et B se sont repoussés, la quantité de mouvement du système est . Les frottements étant négligeables, chaque patineur est soumis à deux forces qui se compensent, son poids et la réaction du sol : le système étudié est isolé.

Dans ce cas , il y a conservation de la quantité de mouvement:   soit   .Les vecteurs quantité de mouvement de A et de B sont opposés :                         .

c. L’égalité précédente se traduit par :  d'où finalement :

Les vecteurs vitesse ont même direction mais des sens opposés.

 Si v_A = 4,0 m×s^-1, v_B = m_A/m_B * v_A = 50/80*4=2,5 m.s^-1.

Exercice 12 page 175:

a. Les trajectoires sont des droites. Les points sont régulièrement répartis : les vitesses sont constantes. A et B sont donc en mouvement rectiligne uniforme.                       

b. La vitesse est v =  d/Dt   , d étant la distance parcourue pendant un intervalle de temps Δt.                      

La distance parcourue par B est plus grande que la distance parcourue par A pendant le même intervalle de temps Δt donc : v_B > v_A.

B est le mobile qui a acquis la plus grande vitesse.

c. Les quantités de mouvement étant égales : p_A = p_B soit m_Av_A=m_Bv_B et si  v_B > v_A, m_B < m_A.

A est le mobile le plus lourd.

Exercice 19 page 178:

a. Le mouvement est rectiligne uniforme si le vecteur vitesse est un vecteur constant                                                  

Le mouvement est étudié dans le référentiel terrestre considéré galiléen.

b. Les actions mécaniques qui s’exercent sur le système constitué par le parachutiste et son parachute sont : l’action exercée par l’air et l’action exercée par la Terre.

c.D’après le principe d’inertie, le mouvement étant rectiligne uniforme, le système est isolé:

  soit

Le poids P est une force verticale dirigée vers le bas, de valeur P = mg ;

                                         P = 90 * 9,8 = 8,8 × 10² N

La force F est une force verticale dirigée vers le haut, de valeur F = P ; F = 8,8 × 10² N.

d. La distance parcourue est d = 400 m et la durée est Dt = 1 min 30 s = 90 s.

La vitesse du parachutiste est v =  d/Dt  soit v=400/90=4,4 m.s^-1 .       .

Exercice 3 page 194 :

La vitesse n’est pas une fonction affine du temps : l’accélération n’est donc pas constante et le mouvement n’est pas uniformément varié.

 

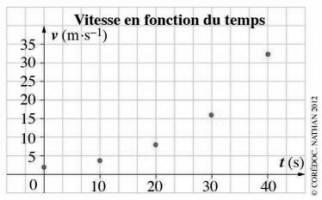Remarque : le mouvement est accéléré.

Exercice 4 page 194 :

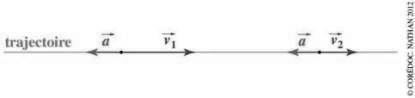
a. La valeur de l’accélération est : a = |DV|/Dt= 2 m.s^-2 .

b. Le mouvement du point est uniformément décéléré : le vecteur accélération est donc de sens opposé au vecteur vitesse. On choisit un sens de déplacement : le vecteur vitesse  a le sens du déplacement et sa valeur diminue alors que le vecteur accélération  est dans le sens opposé au vecteur vitesse  et garde une valeur constante.

 

Exercice 9 page 195:

 

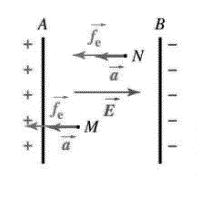a. Le champ  est uniforme ; il est donc identique en M et N. Ce champ est orthogonal aux plaques A et B, son sens est de la plaque portant une charge positive A à la plaque B et sa valeur est :

E=400/0,10= 4000 V.m^-1 .

La force qui s’exerce sur un électron est alors

elle est identique pour un électron en M ou en N. La force  est orthogonale aux plaques A et B, son sens va de la plaque B portant une charge négative à la plaque A et sa valeur fe = 1,6×10^-19 × 4×10³ = 6,4×10^-16 N.

b. et c.  . L’accélération  a donc même direction, même sens que la force électrique et sa valeur est :

a = 6, 4 x10^-16/9,1x10^-31 =7,4.10¹⁴ m.s^-2 .

Exercice 12 page 195 :

Caractéristiques de la particule :

- charge q = +2e = 3,2×10^-19 C ;

- masse m = = 3,35×10^-26 kg.

a. Calcul de la force électrique qui s’exerce sur l’ion :

f_e= (3,1.10^-19*8.10²)/1,2 = 2,1.10^-16 N

b. On applique la deuxième loi de Newton à un ion Ne²⁺ :   soit  

La valeur de l’accélération des ions est alors a = f_e /m=(2,1.10^-16 )/(3,35.10^-26 )=6,3.10⁹  m.s^-2

Exercice 25 page 200 :

Dans l’hypothèse où le mouvement rectiligne de la bille est uniformément varié, alors le vecteur accélération est constant :

Dans un repère (O, ) vertical orienté vers le bas, v = v_y

L’accélération est verticale et a_y =dv_y/dt=dv/dt

La courbe qui passe au mieux entre les points expérimentaux (t,v) est une droite affine d’equation : v_y(t) = at+ β. On a donc a_y=dv/dt=a =cste

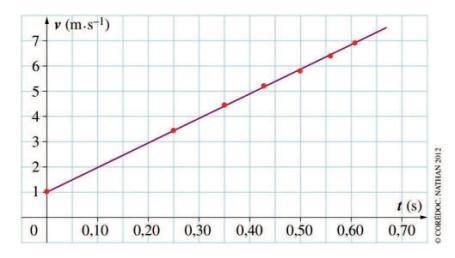
Le mouvement de la bille est bien uniformément varié

Par ailleurs, la vitesse augmente au cours du mouvement (ou les vecteurs vitesse et accélération ont même sens où le produit a_yv_y> 0), on a donc un mouvement uniformément accéléré.

La valeur de l’accélération  le coefficient directeur de la droite. On choisit deux points éloignés sur la droite et on obtient a=(7-2)/0,62=9,7 m.s^-2 .

Exercice 30 page 291:

a. Coordonnées du vecteur vitesse à t₀ = 0 s :

v_0x = v₀cosα   et   v_0z = v₀sinα

b.Le système étudié est la balle. Le référentiel choisi est le référentiel terrestre galiléen.

La balle est soumise à une seule force, son poids. En appliquant la deuxième loi de Newton pour un solide de masse m constante on obtient :

d’où dans le repère proposé : a_x=0 et a_z=-g

c.Par intégration, on obtient les coordonnées du vecteur vitesse :

v_x = C₁ = v₀cosα  ;  v_z = -gt + C₂  soit ici   v_z = -gt + v₀sinα

d.Par intégration, on établit les coordonnées du vecteur position : A t₀=0, on a  x = 0 et z = 0

         x=(v₀cos a) t + C₃     soit ici x =(v₀ cos a)t   car à t₀=0 on a x=0 .

         z=- ½ gt² + (v₀sin a) t + C₄   soit ici z=- ½ gt² + (v₀sin a) t  car à t₀=0 on a z=0

On obtient finalement en éliminant t entre x(t) et z(t) : z = [-gx²/(2v₀² cos²a)] + (tg a) x

e.La vitesse en  S ne peut être nulle, car quelle que soit la position de la balle, elle garde une même vitesse de déplacement horizontale v_x= v₀ cosα.

f.Au point S le vecteur vitesse est tangent à la trajectoire :

v_S,z = 0 s  , soit – gt_S + v₀ sin a =0 d'où t_S= (v₀sin a)/g

d'où 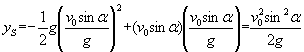  ; c'est la valeur de la flèche

g. La portée du tir correspond à la valeur de la distance OI soit à x_I (abscisse du point d’impact I).

Au point I, on a z_I=0  soit :  pour x différent de 0.

On déduit la portée du tir :

h. calcul de la flèche et de la portée : les calculs donnent  y_S= 4,1 m et x_I= 29 m

i.Ces résultats sont vérifiés avec la simulation .

- Deux tirs ayant la même vitesse de lancement ont la même portée lorsque les angles de tir sont complémentaires.

- La portée est maximale lorsque l’angle de tir est de 45°.