Signaux sonores : caractéristiques
a) Expression mathématique d'un son
Nous allons ici considérer un son , dont nous admettrons que nous pouvons lui associer une expression mathématique :
y=2*sin(2*p*1000*t)+5*sin(2*p*2000*t)
Il s'agit d'un son , somme de deux fonctions sinusoïdales :
-l'une d'amplitude 2 et de fréquence f1=1000 Hz
-l'autre d'amplitude 5 et de fréquence f2=2000 Hz
b)diagramme temporel :
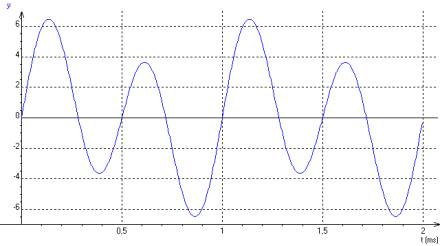
le diagramme temporel de ce signal est représenté ci-dessous ( t en abscisse , y en ordonnée) :

En utilisant les graduations du graphique , nous pouvons observer que la période de ce signal est T = 1ms.
c)diagramme fréquentiel ou spectre
Il est représenté ci-dessous :
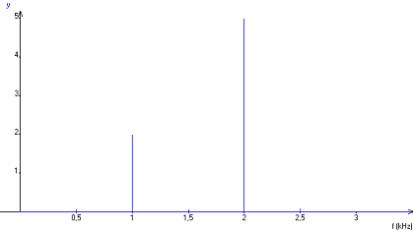
Chaque "bâton" correspond à une composante fréquentielle du signal défini sous forme mathématique plus haut :
f1= 1 kHz
f2= 2 kHz
Les tailles des "bâtons" sont liées aux amplitudes des deux composantes du signal
d)harmoniques :
- fondamental ou harmonique 1 : c'est la composante du signal dont la fréquence est la plus basse . La fréquence du fondamental est ici f1= 1000 Hz.
-harmonique 2 : c'est la composante du signal dont la fréquence est e double de celle du fondamental . Ici la fréquence de l'harmonique 2 est f2=2000 Hz.
e)Série de Fourier :
Soit f une fonction périodique, de période T , on appelle série de Fourier de f, la série :
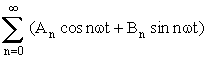 en ayant posé : w=2*p/T
en ayant posé : w=2*p/T
II/Hauteur et timbre d'un son :
a)Hauteur du son :
C'est la fréquence du fondamental soit ici 1000 Hz . Nous remarquons que la période du signal temporel est précisément T=1/f1 = 1/1000= 1 ms , autrement dit , la période d'un signal sonore est égale à l'inverse de la fréquence du fondamental .
b)Timbre d'un son
Il est lié au spectre du signal . Deux sons qui ont le même spectre ont le même timbre.
Remarque : Si deux spectres sont tels que les tailles des "bâtons" sont proportionnelles , le spectres peuvent être considérés comme identiques : les sons correspondants ont le même timbre , mais leur intensité est différente .
III/Intensité du son :
a)Intensité sonore :
L'intensité I (en W/m2) est liée à la puissance sonore P (en W) reçue par une surface S (en m2) :
![]()
b)Niveau sonore :
Le niveau sonore noté L est tel que :
![]()
avec I0= 10-12 W/m2
L se mesure en décibels (dB)
IV/Son pur :
La fonction associée à un son pur est une fonction sinusoïdale (pas d'harmoniques 2 ou supérieurs)
V/Exercices :
* A chercher page 63 : 3,4,5,10,12,18,21
*Exercice résolu page 64