2de physique - TP7 :Mouvement et inertie

Références :

Chapitre 15 pages 230 à 245.

A retenir : l’essentiel page239

Chrono page 240

Exercice résolu page 242 : le parachutiste.

I/Caractère relatif de la trajectoire :

Pour mettre en évidence le caractère relatif du mouvement , nous allons utiliser la vidéo d’un cycliste en mouvent qui laisse tomber une balle qu'il tenait à la main 

A/Acquisition : utilisation de la vidéo :

a)Visualisation de la vidéo

*Double-clic sur le dossier REGRESSI

* Double-clic sur l'icône du logiciel REGAVI

*Sélectionner : "Lecture d'un fichier . AVI".

*Cliquer sur l'icône  pour ouvrir une boîte de Dialogue qui va permettre de sélectionner le fichier veloboul.avi, puis "OUVRIR"

*Si la bicyclette n'est pas sur le côté gauche de l'écran , cliquer sur l'icône  , pour l'y amener .(attention toutes ces icônes se ressemblent !)

*Pour visualiser le mouvement , cliquer sur . On peut visualiser une nouvelle fois le mouvement en ramenant la bicyclette à gauche (click sur ) , puis cliquer à nouveau sur .

b)Echelle :

Il faut informer le logiciel de la correspondance entre les distances réelles et les dimensions de l'image :

*Cliquer sur l'icône  située en haut de l'écran pour définir l'échelle de l'enregistrement .Puis cliquer une première fois (simple click) sur l'axe de la roue arrière et ensuite sur l'axe de la roue avant .Lorsqu'une fenêtre demande ensuite l'échelle "longueur en mètre" , répondre 1 (mètre) , puis Ok

c)Enregistrement :

Nous allons enregistrer les mouvements au cours du temps de deux points particuliers :

- le mouvement du centre de la boule lâchée par le cycliste

- l'axe de la roue avant

On s'eforcera de faire des pointages qui soient les plus précis possibles :

Le mouvement de chacun des points va être rapporté à un repère terrestre (O,x,y) d'origine O .

Il faut faire savoir au logiciel ou se situe cette origine sur l'image :

* Ramener le cycliste sur la gauche

*Cliquer sur l'icône  , viser ensuite la balle et faire un click gauche lorsque la balle est à l'intérieur du viseur .

*Programmer le logiciel pour qu'il retienne deux points par image :

*Cliquer sur  pour lancer les mesures .

*"Prendre" la balle dans le viseur et par un click gauche de la souris , "marquer" la position de la balle .

*"Prendre" l'axe de la roue avant de la bicyclette et par un click gauche de la souris , "marquer" la position de l'axe de la roue avant .

*On passe ensuite automatiquement à l'image suivante. On marque la position de la balle, puis celle de l'axe de la roue avant de la bicyclette comme précédemment .

On effectue ainsi 12 couples de pointages.

*Lorsque les mesures sont terminées , cliquer sur l'icône STOP , puis sur l'icône  qui permet de lancer Regressi . Une fenêtre s'ouvre : cliquer uniquement sur Ok .

B/Les trajectoires : une trajectoire dépend du référentiel .

a)Visualisation des trajectoires :

En principe , les deux trajectoires doivent apparaître à l'écran . Si tel n'est pas le cas , activer la fenêtre graphique en cliquant en haut à gauche de le fenêtre Regressi sur l'icône :.

Il se peut que les différents points des deux trajectoires soient reliés deux à deux par des lignes transversales :pour faire disparaître ces lignes :

*Clic "COORDONNEES" /Plus d'options/mécanique

*Décocher la case "Fil de Fer "

Si besoin est , agrandir la fenêtre en cliquant sur  (en haut à droite de la fenêtre) .

Q1)Représentez sur votre copie les deux trajectoires obtenues , en précisant :

-quelle est celle de la balle

-quelle est celle de l'axe de la roue avant .

Q2)Quelle est la nature de chacune des deux trajectoires (droite , parabole ) ?

b)Trajectoire relative :

Nous allons nous interesser à présent à la trajectoire de la boule par rapport à la bicyclette.

Mathématiquement cela revient à construire la courbe Dy = y1-y2 en fonction de Dx= x1-x2 .

*Activer la fenêtre GRANDEURS en cliquant sur l'icône (en haut à gauche) 

*Click CREER GRANDEUR 

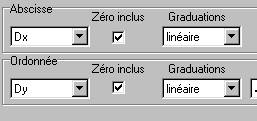
*Compléter la fenêtre comme indiqué ci-contre :

*Ok

*Créer ensuite en procédant de la même façon Dx=x1-x2

Reste à visualiser la courbe Dy=f(Dx)

*Activer la fenêtre GRAPHE 

*Clic COORDONNEES 

*Ajouter 

*Mettre à jour la fenêtre :

* Ok

Q3)Représentez sur votre copie les trois trajectoires . Désigner :

*celle qui correspond au mouvement de la boule par rapport au sol .

*celle qui correspond à la trajectoire de l'axe de la roue avant de la bicyclette par rapport au sol .

*celle qui correspond à la trajectoire de la boule par rapport à la bicyclette . Quelle est la nature de chacune des trajectoires ? Conclure

Quitter Regressi (Fichier/Quitter) . Fermer également les autres fenêtres sans sauver les fichiers.

c)Autre exemple : trajectoire de Mars :

Nous venons de constater que la trajectoire d'un point mobile dépend du référentiel . Nous allons nous interesser à présent à la trajectoire de la planète Mars dans deux cas :

* Le référentiel est le soleil

* Le référentiel est la terre .

*Ouvrir le dossier LOGICIELS (double-click)

*Lancer le programme ASTRO (double-click)

*Appuyer sur F1 : Modèles Hélio <> geo Soleil Terre Mars

*Année de départ : 2005

*Année finale : 2006

*choix du mode : 2 (mode manuel)

*Appuyer ensuite sur la barre Espace (en bas du clavier)

Observer les trajectoires qui se dessinent à l'écran .

Q4)Représentez les schémas sur votre copie . Lequel correspond à la trajectoire de Mars par rapport à la terre ?

Appuyer sur la touche "Echap" du clavier pour sortir et sur F10 pour terminer .

d)Conclusion :

La trajectoire d’un point dépend du référentiel

II/Caractère relatif de la vitesse :

On dispose de deux documents obtenus à la suite de la précédente acquisition (veloboul) :

-un document sur lequel sont représentées la trajectoire de la balle par rapport au sol (A) et la trajectoire de l’axe de la roue (B) avant de la bicyclette par rapport au sol .

-un document sur lequel est représentée la trajectoire de la balle par rapport à la bicyclette (C)

Ces deux documents sont à l’échelle 1/10 .

Q5)1 cm sur le document correspondent à combien de centimètres dans la réalité ?

a)Définition de la vitesse moyenne d’un point en mouvement

la vitesse (moyenne) d’un point en mouvement , par rapport à un référentiel donné est égale au rapport de la distance parcourue « d » par le point , par la durée « Dt » mise par celui-ci pour parcourir cette distance :

Dans le système international , une vitesse se mesure en m.s^-1 .

b)Mesures et calcul

Q6)A partir des deux documents précédents , complétez les tableaux suivant(on indiquera les valeurs des grandeurs indiquées sur la première ligne) :

C2C3 enregistrement

C2C3 réel

V’2,3

C9C10 enregistrement

C9C10 réel

V’9,10

A2A3 enregistrement

A2A3 réel

V2,3

A9A10 enregistrement

A9A10 réel

V9,10

Données :

-échelle au 1/10

-durée entre 2 pointages : Dt = 44 ms

-V’ est une vitesse par rapport au référentiel vélo

-V est une vitesse par rapport au sol

Q7)Comparer V’_2,3 et V_2,3 .Comparer V’_9,10 et V_9,10 . Est-ce que la vitesse dépend du référentiel ?

c)Conclusion relative à la vitesse

La vitesse dépend du référentiel

III/Forces et mouvement

a)Action et force :

L’image ci-contre représente une personne qui porte une valise . Cette action est modélisée , c’est à dire représentée par une force .

Une force est un vecteur (lié):

Un vecteur est caractérisé par sa direction , son sens et sa norme . Si on affecte un point particulier à l’origine du vecteur , on dit qu’il est lié .

Sur l’image , la force modélise l’action du personnage sur la valise. Le point d’application de la force est un point de contact entre la main du personnage et la poignée de la valise .

VIDEO : lesite.tv (forces_sitetv.mp4)

Q8)Représenter la force exercée par la laisse sur le chien

Quels sont :

- la direction de cette force

- le sens de la force

-le point d’application de cette force (origine du vecteur) ?

Q9)Représenter la force exercée par la laisse sur la main du personnage. Quels sont , le point d’application , la direction et le sens de cette force ?

b)Action et mouvement :

Le mouvement d’un corps peut être influencé de 2 manières sous l’action d’une force :

-modification de la trajectoire

-modification de la vitesse

VIDEO : Dailymotion

c)Les types de forces :

On distingue deux types de forces (ou d’actions) :

*les forces à distances . Ce sont :

-les forces électriques Exemple : une règle frottée avec un tissu attire de petits bouts de papier lorsqu’on approche la règle.

-magnétiques : actions entre aimants par exemple .

-gravitationnelles : le poids d’un corps (le poids d’un objet résulte de l’attraction que la terre exerce sur cet objet).

*les forces de contact. Ces forces nécessitent qu’il y ait contact entre les objets qui interagissent.

Remarque : les actions à distance ne nécessitent pas qu’il y ait de contact entre les objets qui interagissent.

Parmi les forces de contact , nous distinguerons :

- les contacts sans frottements

La force de contact est perpendiculaire aux surfaces en contact .

Sur le schéma représente l’action du support sur l’objet lorsqu’il n’y a pas de frottements.

Q10)Reproduire le schéma ci-dessus et représenter l’action de l’objet sur le support (lorsqu’il n’y a pas de frottements)

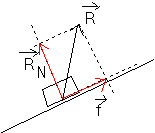
-les contacts avec frottements

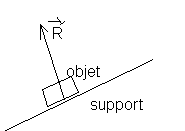
Sur le schéma ci-contre , on représente par exemple l'action de contact qu'exerce un support incliné sur un objet en mouvement vers le bas .

Un vecteur peut toujours être considéré comme la somme vectorielle de deux vecteurs et ici , nous pouvons écrire :

avec pour les vecteurs les propriétés suivantes :

-  est tangente aux surfaces en contact

-  est perpendiculaire aux surfaces en contact

est appelée force de frottement (lorsqu'il y a mouvement , elle est opposée au vecteur vitesse)

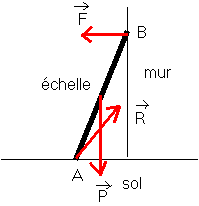
d)Exemple : échelle contre un mur

L'action de contact entre l'échelle et le mur est supposée sans frottement .

L'échelle est soumise à :

* une action à distance : l'action de la terre sur l'échelle , le poids de l'échelle . Le point d'application de cette force est le centre de gravité (ou centre d'inertie) de l'échelle)

Il n'y a pas d'autres actions à distance .

* deux actions de contact , car il y a deux contacts .

- L'action du mur sur l'échelle  . Le contact étant sans frottement , la force est perpendiculaire au mur .

-l'action du sol sur l'échelle : le contact est avec frottement (sinon l'échelle ne peut ps être immobile ) et par conséquent , cette force n'est pas perpendiculaire au sol .

trajectoires sont différentes : nous constatons là encore que la trajectoire dépend du référentiel .

e)Mesure de la valeur (ou intensité ) d’une force :

Pour mesurer la valeur d’une force , nous pouvons utiliser un dynamomètre

Q11)On suspend une masse m à un dynamomètre m=......... Quelle est la valeur indiquée par le dynamomètre (dans le système international , une force se mesure en newtons (N)

IV/Principe d’inertie

a)Condition d’équilibre d’un solide :

Pour qu’un solide soit en équilibre , il faut nécessairement que la somme vectorielle des forces qui lui sont appliquées soit nulle.

Dans l’exemple de l’échelle ci-dessus , cela s’écrit :

b)Principe d’inertie :

Nous pouvons nous poser la question suivante : Si la somme vectorielle des forces appliquées à un solide est nulle , le solide est-il pour autant en équilibre ? la réponse est non !

Que dit le principe d’inertie ?

Si les forces qui s’exercent sur un solide se compensent (somme vectorielle nulle) :

-son centre de gravité (ou son centre d’inertie) reste au repos s’il n’a pas de vitesse initiale .

-son centre de gravité a une mouvement rectiligne (la trajectoire est une droite) uniforme (sa vitesse est constante) s’il possède une vitesse initiale .

Réciproquement, si un corps est au repos ou si son centre de gravité a un mouvement rectiligne uniforme , les forces qui s’exercent sur lui se compensent (leur somme vectorielle est nulle)

c)Expérience : mise en évidence du centre d’inertie :

-objets sur table soufflante

- VIDEO : CentreInertie.swf

V/Exercices :

Page 240 et suivantes : 4 ,5,8, 11, 12 13 (sauf a), 15, 19 (sauf d) , 23 et 28 (sauf d)

TP7 physique - 2de - Mouvement et inertie -correction

1)

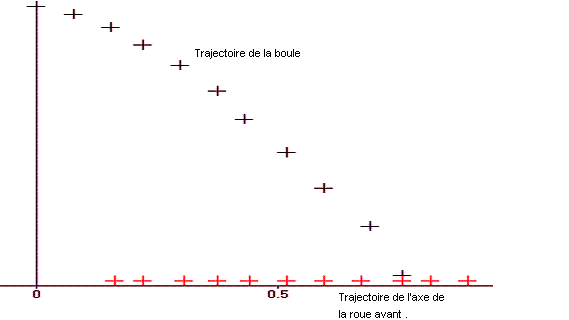
2)La boule a une trajectoire parabolique

La trajectoire de l'axe de la roue est une droite .

3)

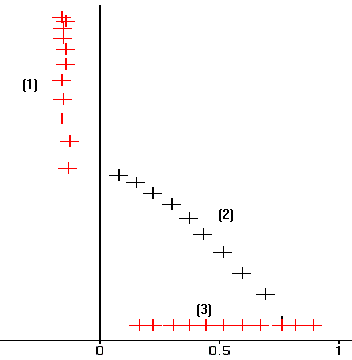
(1) : Dy = f(Dx) : trajectoire de la boule par rapport à la bicyclette . C'est une droite

(2) : trajectoire de la boule par rapport au sol . C'est une parabole .

(3) : trajectoire de l'axe de la roue par rapport au sol .

Pour les courbes (1) et (2) , il s'agit de la trajectoire de la boule dans des référentiels différents . Ces deux courbes sont différentes , autrement dit , la trajectoire d'un "objet " dépend du référentiel .

4)

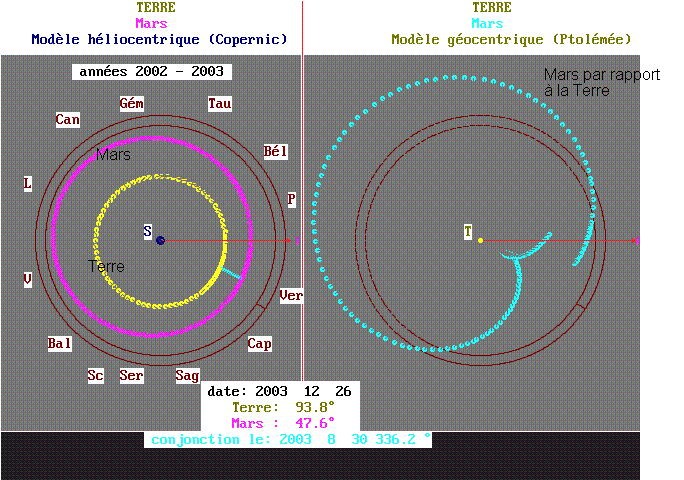
La fenêtre de gauche montre les trajectoires de la Terre et de Mars par rapport au référentiel .

La fenêtre de droite montre la trajectoire de Mars par rapport à la terre . Il est évident que ces deux trajectoires sont différentes : nous constatons là encore que la trajectoire dépend du référentiel .

5)A l’échelle 1/10 , 1 cm sur le document correspond à 10 cm dans la réalité .On écrira :

1 cm <----> 10 cm

6)

C2C3 enregistrement	C2C3 réel	V’2,3	C9C10 enregistrement	C9C10 réel	V’9,10
0,95 cm	9,5 cm	216 cm/ms	1,8 cm	18 cm	409 cm/ms

A2A3 enregistrement	A2A3 réel	V2,3	A9A10 enregistrement	A9A10 réel	V9,10
1,1 cm	11 cm	250 cm/ms	2 cm	20 cm	454 cm/ms

7)V’_2,3 est différent de V_2,3 et V’_9,10 est différent de V_9,10 . Autrement dit , la vitesse dépend du référentiel . La vitesse de la balle est plus importante dans le repère terrestre (sol) que dans le repère du vélo .

8)

-direction de la force : celle de la laisse

-sens : du chien vers le personnage

-point d’application : contact laisse-collier

9)

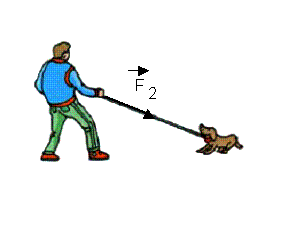
-direction de la force : celle de la laisse

-sens de la force : vers le chien

-point d’application : contact main-laisse.

10)

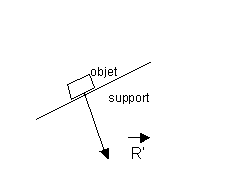
L’action de l’objet sur le support est l’opposée de l’action du support sur l’objet , d’où la représentation ci-dessus 

11)Si m=100 g = 0,1 kg , le dynamomètre indique 1 N . Ce résultat est en fait en rapport avec la relation entre poids et masse qui a été vue en collège P=m*g , avec g=10 N.kg^-1 .

Avec cet exemple nous avons P = 0,1*10 = 1 N.