REFRACTION

TP 2de : REFRACTION

Objectif : Etudier expérimentalement la loi de Descartes sur la réfraction.

l/Mise en évidence du phénomène de réfraction.

a)Expérience 1

Placer une pièce au fond d'un récipient opaque. S'éloigner de la tasse jusqu'à ce que la pièce

ne soit plus visible. Une deuxième personne verse de l' eau dans le récipient.

Q1)Qu'observe la première personne quand il y a suffisamment d'eau dans le récipient ?

b)Expérience 2 :

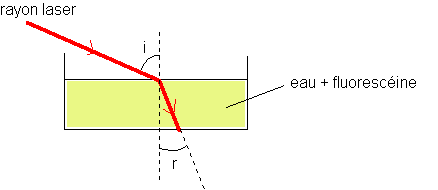
Q2)Décrire le comportement du rayon laser . Se propage t-il en ligne droite ?

Q3)A partir de cette expérience , justifier l'observation de l'expérience précédente (faire un schéma)

II/Etude de la loi de Descartes sur la réfraction.

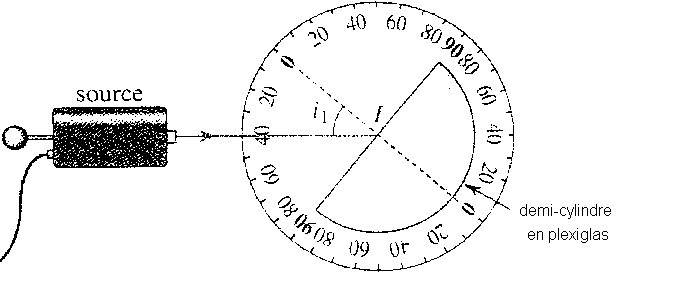
Matériel : - Une source de lumière blanche équipée d'une fente de sortie permettantd'obtenir un fin pinceau lumineux.

- Un hémicylindre de Plexiglas monté sur un disque gradué en degrés.

Eclairer l'hémi-cylindre sur la face rectangulaire avec un pinceau de lumière dirigé vers son centre .

Q4)Comment peut-on repérer l'angle d'incidence et l'angle de réfraction ?Dans quels milieux les rayons lumineux se propagent-ils ?

Q5)Faire arriver le faisceau incident perpendiculairement à la face plane. Décrire les

observations.

Q6)Faire arriver le faisceau sous l'incidence i et mesurer la valeur r de l'angle de réfraction.

Complétez sur votre copie un tableau analogue au tableau suivant :

i (en °)	0	10	20	30	40	50	60	70	80
r (en °)
sin i
sin r

Q7)Pourquoi le faisceau qui traverse la face cylindrique du bloc n'est-il pas dévié ?

Q8)Tracer sur papier millimétré la courbe représentant l'angle de réfraction en fonction de

l'angle d'incidence.Y a-t-il une relation de proportionnalité entre i et r ?

Q9)Tracer la courbe représentant sin r en fonction de sin i. En déduire une relation entre sin r et sin i.

Cette relation est une loi de Descartes sur la réfraction : sin i = n sin r

Q10)Déterminer l'indice de réfraction n du Plexiglas en exploitant la courbe précédente ..

TP 2de : Réfraction (correction)

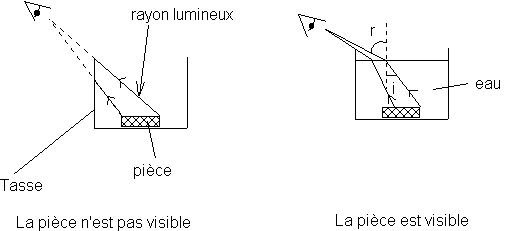
1)Lorsqu'il y a suffisamment d'eau dans le récipient , la première personne voit la pièce qui auparavant n'était pas visible .

2)Le rayon laser se propage en ligne droite dans l'air . Lorsqu'il atteint la surface de l'eau , il change de direction . Dans l'eau , le rayon laser est rectiligne , mais sa direction est différente de celle du rayon dans l'air .

3)Le phénomène de réfraction permet d'expliquer l'expérience précédente "de la pièce" :

L'angle d'incidence i est l'angle que fait le rayon incident avec la normale au dioptre plan air/plexiglas

L'angle de réfraction est l'angle que fait le rayon réfracté avec la normale au dioptre .

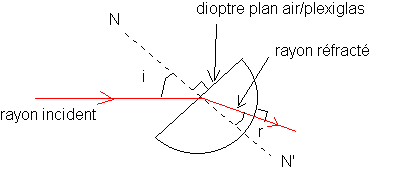
NN' : normale au dioptre plan

Le rayon incident se propage dans l'air

Le rayon réfracté se propage dans le plexiglas .

5)Dans ce cas de figure (rayon incident perpendiculaire au dioptre plan , c.à d. i=0) , le rayon lumineux n'est pas dévié , autrement dit , il a la direction NN' .

i (en °)	10	20	30	40	50	60	70	80
r (en °)	7	13	19,5	25	31	35	38	40
sin i	0,17	0,34	0,5	0,64	0,76	0,86	0,94	0,98
sin r	0,12	0,22	0,33	0,42	0,51	0,57	0,61	0,64

Le rayon qui traverse la face cylindrique du bloc n'est pas dévié car ce rayon est toujours perpendiculaire au dioptre cylindrique plexiglas/air (se reporter à la question Q5)

La courbe obtenue n'est pas une droite : il ne peut donc pas y avoir proportionnalité entre i et r .

Posons x= sin i et y= sin r . y est une fonction linéaire de x , donc de la forme y=ax . a est le coefficient directeur de la droite .

Le point M appartient à la droite : ses coordonnées vérifient donc l'égalité (sin r)_M = a * (sin i)_M . En remarquant sur le graphique que (sin r )_M = 0,4 et (sin i )_M = 0,6 , nous obtenons a = (sin r )_M /(sin i )_M =0,4/0,6 =0,65 .

10)Nous pouvons aussi écrire :

Nous retrouvons bien la seconde loi de Descartes relative à la réfraction :

n_air sin i = n_plexiglas * sin r

avec n_air= 1 (indice de réfraction de l'air) et n =n_plexiglas =1,5 (indice de réfraction du plexiglas .