DETERMINATION DU RAYON DE LA TERRE - ERATOSTHENE - TP 2de

I/Objectif :

Déterminer le rayon d'une sphère en utilisant la méthode d'Eratosthène

II/Eratosthène :

Sur le bureau de l'ordinateur , ouvrir le dossier "Travaux Pratiques " (double-clic) et le sous-dossier "Eratosthene". Double-clic sur "Document"

Q1)Quelle est l'hypothèse émise par Aristarque de Samos ?

Q2)Qui était Eratosthène , quelle était son activité ?Qu'a t-il proposé ?

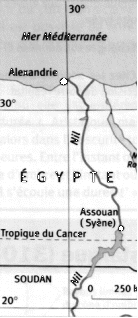
Q3)Quelles sont les deux villes "utilisées" par Eratosthène pour réaliser son expérience ?Mettre en rouge ces deux villes sur le document ci-contre .

Q4)Ces deux villes sont-elles situées sur le même méridien ?

Q5)Que signifie l'expression :"le soleil est au zénith" ?

III/Détermination du rayon de la terre :

a)Expérience :

On utilise une sphère en polystyrène avec deux petits bâtons . L'ensemble est éclairé par un rétroprojecteur . Les rayons lumineux envoyés par le rétroprojecteur sont parallèles .

Q6)Décrivez en vous appuyant sur le schéma ci-dessous , l'expérience réalisée .

Q7)Justifiez l'égalité des angles a et b .

Q8)Définir "l'ombre portée"

Nous admettrons que :

Autrement dit , la connaissance de AB (distance entre deux villes situées sur le même méridien), de BC' (ombre portée) et h (hauteur du bâton) , nous permettent d'en déduire R (rayon de la sphère)

b)Mise en évidence par simulation de l'ombre portée

A partir du sous-dossier "Eratosthène" , lancer (double-clic) "Gnomon"

Avec la souris , ajuster la date au 180 eme jour environ .

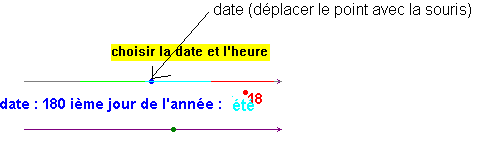
En déplaçant avec la souris le point de l'axe des heures , on met en évidence l'évolution de l'ombre du gnomon (bâton) au cours de la journée .

c)Rayon de la terre :

* distance entre les deux villes (distance AB): 5000 stades (1 stade = 157 m)

* b=7 °

Q9)Sachant que a*R = , a étant exprimé en radians , calculer le rayon terrestre R . Donner la valeur de R en km .

IV/Exercice complémentaire :

Nous reprenons la figure de la question Q6 .

h=8m ; BC'=1 m . Claculer tan a et en déduire la valeur numérique de a . Comparer la valeur numérique de a exprimé en radians et la valeur numérique de la tangente .

TP3 : Eratoshène - CORRECTION

1)Aristarque de Samos émet l’hypothèse que la Terre est ronde .Il justifie cette hypothèse à partir d'expériences astronomiques (notament la forme du cône d’ombre sur la Lune pendant une éclipse de Lune).

2)Eratosthène est né à Cyrène en Libye .Il était t directeur de la grande bibliothèque d'Alexandrie en 236 avant J.C .Il a proposé de déterminer par une méthode géométrique la taille de la terre .

3)Les deux villes "utilsées" par Eratosthène pour réaliser son expérience sont Alexandrie et Syène , en Egypte

4)La carte fait apparaître que les deux villes ne sont pas situées sur le même méridien , contrairement à ce que pensait Eratosthène .

5)Dire que le "soleil est au zénith" en un lieu donné , signifie qu'il est à la verticale de ce lieu . Lors de l'expérience d'Eratosthène , à Syène , le soleil était au zénith .

6)Le soleil étant très éloigné de la terre , on peut admettre que les rayons du soleil reçus par la Terre sont parallèles entre eux .

On considère deux villes A et B situées sur le même méridien . Si en A , le soleil est au zénith ,un bâton planté verticalement dans le sol n'aura pas d'ombre (ombre portée) .En B , par contre , si le soleil n'est pas au zénith , à cause de la sphéricité de la terre, un bâton planté verticalement aura une ombre (notée BC' sur le schéma).

L'idée d'Eratosthène fut de mesurer "la longueur" l'ombre portée en B et connaissant la distance entre les deux villes (5000 stades) , ainsi que la taille du bâton , d'en déduire le rayon terrestre .

7)a et b sont des angles alternes-internes : ils sont donc égaux .

8)L'ombre portée est l'ombre due à l' objet lorsqu'il est éclairé par le soleil (ou toute autre source lumineuse)

9) égalité de conversion : p radian = 180 ° ou 1°= p/180 rad

Et donc 7° = 7p/180 rad = 0,12 rad .

R= AB/a = (5000*157)/0,12=6,54.10⁶ m =6540 km

Exercice complémentaire :

Or nous avons trouvé a= 0,12 rad . Autrement dit tang a = a_radians (approximation des petits angles)

Remarque : Dans tous ces calculs , nous avons confondu la corde BC et l'arc , ce qui est tout à fait acceptable dans le cadre des petits angles .