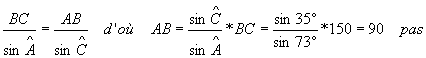TP 2 : Mesures de longueurs.
Problème : Comment mesurer la taille ou la distance qui nous sépare d’objets lointains ?
I/ Rappel du théorème de Thalès.
Enoncé :

Application : on donne AN = 1,5 m, AC = 4,9 m et MN = 2,3 m. Donne l’expression littérale de BC puis calcule sa valeur.
II/ Mesure de la taille d’objets lointains.
1) Manipulation : méthode de la visée.
Objectif : appliquer la méthode de la visée pour mesurer la hauteur d’un objet (on cherche à mesurer la hauteur H d’une éprouvette graduée )
Protocole expérimental :
L’éprouvette graduée est placée sur la bureau ( côté mur ou côté fenêtre ).
*Tenir, verticalement, à bout de bras une règle graduée.
*Fermer un oeil et placer l’autre de façon à faire coïncider la graduation zéro de la règle avec le bas de l’éprouvette graduée
*Noter la graduation qui coïncide avec l’extrémité supérieure de l’éprouvette graduée. Soit h la portion de règle utilisée.
*Faire mesurer par le binôme la distance d séparant les yeux de la règle.
*Mesurer la distance D séparant l’éprouvette graduée de votre œil du bord de la table.
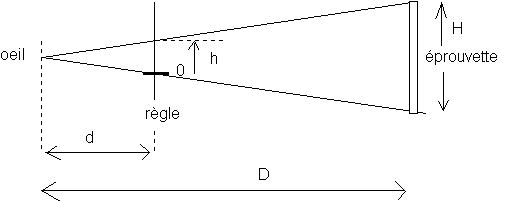
Q1) Exprimer H en fonction de d, D et h
Q2)Noter les valeurs numériques de d,D et h . Déterminer la hauteur H de l'éprouvette .
Q3)Comparer la hauteur H trouvée à la valeur de H mesurée directement Hdirecte et en déduire l'incertitude relative
2)Diamètre apparent de l'éprouvette :
On appelle diamètre apparent d’un objet l’angle a sous lequel on voit cet objet depuis un point.
Q4)Faire apparaître sur un schéma le diamètre apparent de l’éprouvette graduée. En utilisant les
relations trigonométriques, calculer sa valeur en degré.
III/Etude d’un document : utilisation des ombres portées.
Objectif : découvrir la méthode utilisée par Thalès pour déterminer la hauteur d’une pyramide.
Document :

« Le mathématicien grec Thalès (625 av. J.C. – 546 av. J.C.) aurait formulé son célèbre théorème en voulant mesurer la hauteur des pyramides de Gizeh. Thalès utilisa un gnomon, c’est-à-dire un bâton droit de hauteur h, qu’il planta verticalement dans le sol. Eclairé par les rayons du soleil supposés parallèles, le gnomon projetait une ombre de longueur d.
Thalès mesura d ainsi que la longueur D de l’ombre d’une pyramide. Il en déduisit la hauteur H de cette dernière. »
Q5) Dessiner la figure correspondant à l’application du théorème de Thalès. Désigner les sommets des deux triangles par des lettres. En comparant cette figure au document ci-dessus, fais figurer les longueurs d, h, D et H du problème.
Q6)Donner l’expression littérale de H en fonction de d, h et D.
Q7)La pyramide est celle de Kheops . Calcule sa hauteur sachant que : d = 27 cm, h = 1,5 m et D = 25 m.
IV/Questions complémentaires :
1)Quelle est l'unité légale de longueur ?
2)Qu'est-ce que le diamètre apparent d'un objet ?
3)Exercice 15 page 32
TP2 : Mesure des longueurs - CORRECTION :
1)
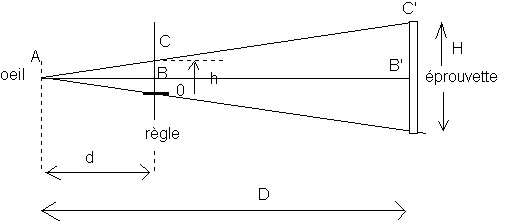
On applique le théorème de Thalès aux tringles ABC et AB'C' : ![]()
Cette égalité s'écrit aussi :![]() et donc finalement :
et donc finalement : ![]()
2)Les mesures effectuées dépendent de la place du "groupe" dans la classe (D) et de la longueur des bras de l'opérateur (d) .
3)Hdirecte =30 cm
L'incertitude relative ne doit pas dépasser 10 % (dans le cas contraire , c'est que les mesures ont été mal faites !)
4)
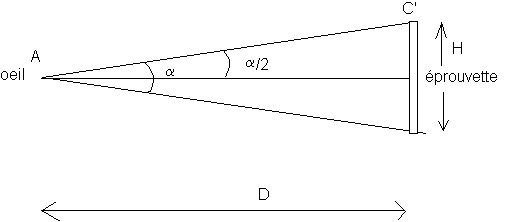
![]()
Exemple : pour un élève situé à 6 mètres de l'éprouvette (D=6 m) tan(a/2)=0,30/6= 0,05
A la calculette , on obtient a/2 = tan-1(0,05) = 2,8 ° = 0,05 rad
(On remarque que la tangente est pratiquement égale à la valeur de l'angle exprimée en radians . Cette approximation n'est valable que pour les petits angles(<10°)) .
Finalement a= 5,6 ° = 0,1 rad .
5)
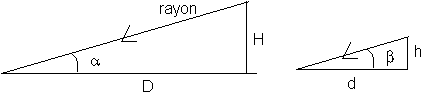
6)Les rayons du soleil étant parallèles a=b et donc :
![]() et finalement
et finalement ![]()
7)Application numérique :
H=1,5*25/0,27 = 139 m
Questions complémentaires :
1)L'unité de longueur légale est le mètre (m)
2)Le diamètre apparent d'un objet est l'angle sous lequel on voit cet objet .
3)Exercice 15 page 32 :
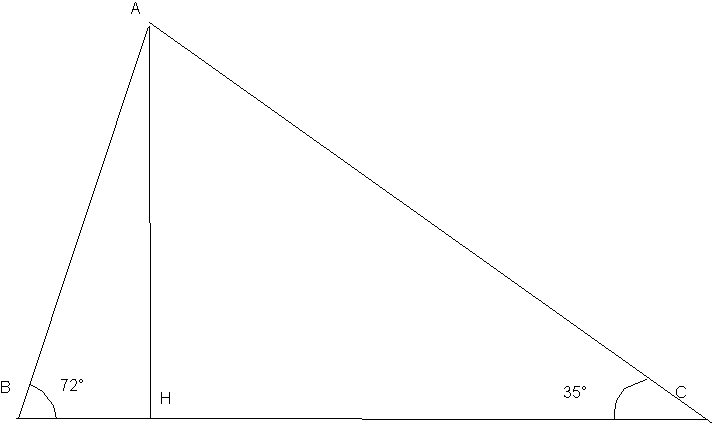
2)BC =150 pas = 17 cm sur le graphique
AB=10,3 cm sur le graphique
Or 1 cm sur le graphique= 150/17=8,8 pas et par conséquent AH= 10,3*8,8=90 pas.
Aurélie est donc située à 90 pas du clocher .
3)D'après le graphique :
![]()
![]() BC=BH+HC
BC=BH+HC ![]()
De ces égalités nous déduisons :
![]()
![]()
![]() et donc finalement :
et donc finalement :
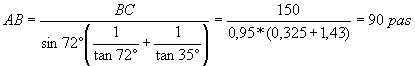
Autre méthode :
L'angle ![]() est égal à 180-(72+35)=73°
est égal à 180-(72+35)=73°
Les relations dans le triangle ABC :