
DE LA CHUTE LIBRE AU SATELLITE
I/Objectifs
*Montrer que la mise en orbite d'un satellite a un rapport avec le mouvement de chute libre avec vitesse initiale .
* Mettre en évidence l'influence de la force d'attraction gravitationnelle .
II/"Lancement " d'un objet
*Ouvrir le dossier LOGICIELS (double-click)
*Lancer IP (double-click)
*Agrandir les fenêtres 
*Fichier/ouvrir/decol.ip
La sphère centrale représente la terre (masse MT= 6.1024 Kg) , la petite sphère (bleue) correspond à un objet S au niveau du sol .
Nous allons faire "décoller" l'objet S en agissant sur :
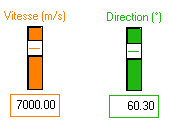
* la vitesse de décollage : V (vitesse)
*l'angle de décollage par rapport à " l'horizontale" (direction)
La vitesse peut varier entre 0 et 10 km/s en agissant sur le curseur Vitesse (orange)
L'angle peut varier entre 0 et 90 ° en agissant sur le cirseur Direction (vert)
On pourra observer les résultats obtenus pour les conditions initiales qui sont regroupées dans le tableau suivant :
| Cas | Vitesse | Direction |
| 1 | 1000 | 0 |
| 2 | 1000 | 45 |
| 3 | 5000 | 45 |
| 4 | 5000 | 90 |
| Cas | Vitesse | Direction |
| 5 | 7000 | 45 |
| 6 | 7600 | 60 |
| 7 | 7600 | 70 |
| 8 | 7600 | 81 |
Déroulement de chaque simulation
*Click REINIT
*Click Effacer Traces
*Réglage des curseurs
*EXEC ..... ARRET
Q1)Pour chaque cas , faites part de vos observations sur votre copie et réprésentez pour quelques cas les trajectoires observées .
Quelle conclusion tirez vous de ces observations ?
Q2)La simulation prend t-elle en compte d'éventuels frottements entre S et la terre ? Justifiez votre réponse .
III/Satellite :

Les simulations précédentes nous ont montré que l'objet revient en général (si la vitesse n'est pas trop grande) vers le sol .
Pour mettre un objet en orbite , il faut en fait procéder en deux temps :
1-décollage en donnant une impulsion à l'objet (![]() )
)
2-mise en orbite en communiquant à l'objet une seconde impulsion qui a
pour effet de modifier la trajectoire de l'objet) (![]() )
)
Nous allons à présent nous interesser à la phase 2:
*Fichier/fermer Si le logiciel vous demande si vous voulez sauver le fichier , cliquez NON
*Fichier/ouvrir/satellit.ip (agrandir au maximum la fenêtre si nécessaire ).
Comme précedemment , les deux curseurs permettent de faire varier
l'intensité de ![]() et sa direction par
rapport à "l'horizontale" (qui peut varier ici entre -90° et + 90°)
et sa direction par
rapport à "l'horizontale" (qui peut varier ici entre -90° et + 90°)
On pourra envisager les cas suivants :
Cas |
Vitesse |
direction |
||
1 |
0 |
0 |
||
2 |
5000 |
-90 |
||
3 |
5000 |
+90 |
||
4 |
3000 |
+90 |
||
5 |
3000 |
0 |
||
6 |
5000 |
0 |
||
7 |
4500 |
0 |
||
8 |
4000 |
0 |
||
9 |
4000 |
-20 |
||
Le déroulement de la simulation s'effectuera comme dans II
Q3)Quelles sont vos observations et vos conclusions ?Le satellite reste t-il en orbite quelle que soit la vitesse initiale ?Y a t-il un ou des cas où le satellite s'éloigne indéfiniment de la terre ? Détaillez votre réponse .
Q4)Essayez de déterminer la vitesse initiale du satellite pour que son orbite soit circulaire
Q5)A quelle force est soumis le satellite ?.Que deviendrait le mouvement du satellite si cette force disparaissait ?
Q6)Quelle est la valeur en km.h-1 de V=5 km/s ?
Q7)Un satellite en orbite consomme t-il du carburant ?
Q8)Que pensez vous de l'affirmation : "Le satellite en orbite est en chute libre . Il tombe vers la terre sans jamais la rencontrer" ?
IV/Deux satellites :
Nous allons nous interesser aux mouvements simultanés de deux satellites et visualiser , comme cela a déjà été fait dans un précédent TP, la trajectoire de l'un relativement à l'autre :
*Fichier/fermer Si le logiciel vous demande si vous voulez sauver le fichier , cliquez NON
*Fichier/ouvrir/2satel.ip (agrandir au maximum la fenêtre si nécessaire ).
Ici la terre n'est pas visualisée (On devine cependant la position de son centre) .
a)Trajectoires des satellites dans le repère géocentrique :
Q9)Rappelez la définition du repère géocentrique .
On pourra envisager les cas suivants :
Cas |
V1 |
Dir 1 |
V2 |
Dir2 |
1 |
4000 |
0 |
4000 |
0 |
2 |
3000 |
0 |
4000 |
0 |
3 |
4500 |
0 |
4500 |
180 |
4 |
||||
5 |
||||
6 |
Les cases libres sont laissées à votre initiatives
Q10)Quelles sont les natures des trajectoires des satellites dans le repère géocentrique ?
b)Trajectoire de satellite 1 par rapport à satellite 2 :
*Effacer Traces
*REINIT
Régler les curseurs : V1 = 4400 m/s Dir1 = 0°
V2= 4400 m/s Dir 2=0°
*Cliquer sur le bouton SATELLITE 2 (Satellite 2 sert alors de référentiel - on pourra revenir au repère géocentrique en cliquant sur TERRE)
*EXEC ... ARRET
Q11)Conclure .
Correction du TP : de la chute libre au satellite :
1/cas 1 (par exemple) : vitesse faible , verteur vitesse initial tangent au sol (direction 0 °):

Le satellite tourne autour de la terre en restant en contact avec le sol .

Cas 3 : vecteur vitesse initial incliné de 45° par rapport à l'horizontale . Le satellite est lancé (comme une pierre) et retombe sur le sol .
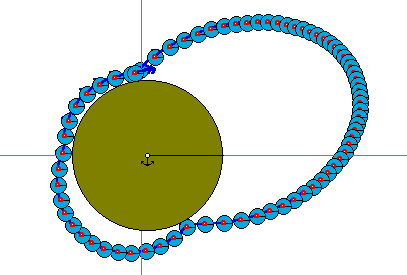
cas 5 :
Dans tous les cas envisagés , le satellite quitte le sol et reprend contact avec le sol .
2/La simulation ne prend pas en compte les frottements entre S et la terre , car sinon le satellite s'arrêterait "de lui-même" sur le sol , ce qui n'est pas le cas (pour que le satellite s'arrête , il faut cliquer sur le bouton "arrêt".
3/cas 1 : mouvement de chute libre sans vitesse initiale , mouvement rectiligne (pas de mise en orbite)
cas 2: chute libre avec vitesse initiale verticale , mouvement rectiligne
cas 3 et 4 : chute libre avec vitesse initiale verticale . Dans le cas 3 le S "s'élève" davantage que dans le cas 4 . S s'élève d'abord et redescend ensuite .
cas 5 : S touche le sol (vitesse insuffisante pour être satellisé)
cas 6,7 , 8 et 9 : S est satellisé
cas 10 : direction 0° , vitesse=10000 m/s : S s'éloigne indéfiniment de la terre .
4/direction : 0° , vitesse = 4200 m/s : dans ce cas l'orbite de S est circulaire .
5/Le satellite est soumis à la force gravitationnelle : ![]() où mS est la masse de S , mT la masse de la terre et d la distance entre le centre de la terre et le
satellite . C'est la seule force appliquée au satellite . Si celle-ci disparaissait le
satellite aurait un mouvement rectiligne uniforme (principe d'inertie)
où mS est la masse de S , mT la masse de la terre et d la distance entre le centre de la terre et le
satellite . C'est la seule force appliquée au satellite . Si celle-ci disparaissait le
satellite aurait un mouvement rectiligne uniforme (principe d'inertie)
6/ 1 h=3600 s et donc ![]()
Donc
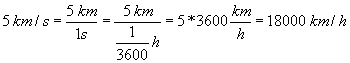
7/Un satellite en orbite ne consomme pas de carburant . Le satellite tourne autour de la terre sans la mise en marche de moteurs qui dépenseraient de l'énergie .
8/L'affirmation est exacte .
9/Le repère géocentrique a son origine au centre de la terre et ses trois axes sont orientés vers trois étoiles fixes .
10/ Dans le repère géocentrique , les deux satellites ont des trajectoires elliptiques .
11/
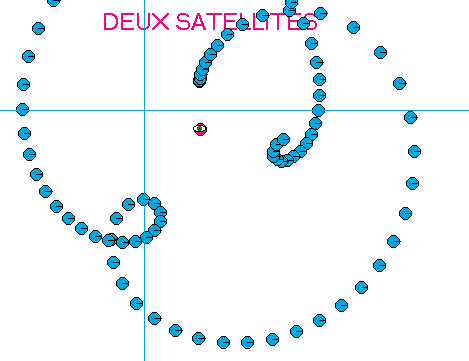
La trajectoire du satellite 1 par rapport au satellite 2 n'a plus rien d'elliptique : pas étonnant , car nous savons que la trajectoire d'un objet en mouvement dépend du référentiel .