pour ouvrir une
boîte de Dialogue qui va permettre de sélectionner le fichier veloboul.avi, puis
"OUVRIR"EXAO - RELATIVITE DU MOUVEMENT - TP 2de
I/But du TP
Mettre en évidence que la trajectoire d'un point mobile dépend du référentiel .
II/La vidéo :
Un cycliste en mouvent laisse tomber une balle qu'il tenait à la main .
a)Visualisation de la vidéo
*Double-click sur le dossier REGRESSI
* Double-click sur l'icône du logiciel REGAVI
*Sélectionner : "Lecture d'un fichier . AVI".
*Cliquer sur l'icône pour ouvrir une
boîte de Dialogue qui va permettre de sélectionner le fichier veloboul.avi, puis
"OUVRIR"
*Si la bicyclette n'est pas sur le côté gauche de l'écran , cliquer
sur l'icône 
, pour l'y amener .(attention toutes ces icônes se
ressemblent !)
*Pour visualiser le mouvement , cliquer sur 
.
On peut visualiser une nouvelle fois le mouvement en ramenant la bicyclette à gauche
(click sur ) , puis cliquer à nouveau sur .
b)Echelle :
Il faut informer le logiciel de la correspondance entre les distances réelles et les dimensions de l'image :
*Cliquer sur l'icône 
située en haut de
l'écran pour définir l'échelle de l'enregistrement .Puis cliquer une première fois
(simple click) sur l'axe de la roue arrière et ensuite sur l'axe de la roue avant
.Lorsqu'une fenêtre demande ensuite l'échelle "longueur en mètre" , répondre
1 (mètre) , puis Ok
c)Enregistrement :
Nous allons enregistrer les mouvements au cours du temps de deux points particuliers :
- le mouvement du centre de la boule lâchée par le cycliste
- l'axe de la roue avant
On s'eforcera de faire des pointages qui soient les plus précis possibles :
Le mouvement de chacun des points va être rapporté à un repère terrestre (O,x,y) d'origine O .
Il faut faire savoir au logiciel ou se situe cette origine sur l'image :
* Ramener le cycliste sur la gauche
*Cliquer sur l'icône 
, viser ensuite la
balle et faire un click gauche lorsque la balle est à l'intérieur du viseur .
*Programmer le logiciel pour qu'il retienne deux points par image :
*Cliquer sur 
pour lancer les mesures .
*"Prendre" la balle dans le viseur et par un click gauche de la souris , "marquer" la position de la balle .
*"Prendre" l'axe de la roue avant de la bicyclette et par un click gauche de la souris , "marquer" la position de l'axe de la roue avant .
*On passe ensuite automatiquement à l'image suivante. On marque la position de la balle, puis celle de l'axe de la roue avant de la bicyclette comme précédemment .
On effectue ainsi 12 couples de pointages.
*Lorsque les mesures sont terminées , cliquer sur l'icône STOP , puis
sur l'icône 
qui permet de lancer Regressi . Une fenêtre
s'ouvre : cliquer uniquement sur Ok .
III/Les trajectoires :
a)Visualisation des trajectoires :
En principe , les deux trajectoires doivent apparaître à l'écran .
Si tel n'est pas le cas , activer la fenêtre graphique en cliquant en haut à gauche de
le fenêtre Regressi sur l'icône :
.
Il se peut que les différents points des deux trajectoires soient reliés deux à deux par des lignes transversales :pour faire disparaître ces lignes :
*Click "COORDONNEES" 
/Plus
d'options/mécanique
*Décocher la case "Fil de Fer "
Si besoin est , agrandir la fenêtre en cliquant sur 
(en haut à droite de la fenêtre) .
Q1)Représentez sur votre copie les deux trajectoires obtenues , en précisant :
-quelle est celle de la balle
-quelle est celle de l'axe de la roue avant .
Q2)Quelle est la nature de chacune des deux trajectoires (droite , parabole ) ?
b)Animation :
Regressi permet de revoir l'animation en visualisant uniquement les trajectoires des points concernés .
*Cliquer sur le menu OPTIONS /Graphique
Ajuster la taille des points à 8 : 
/Ok
Si la taille des points ne change pas click COORDONNEES et refermer la fenêtre en cliquant Ok
*Cliquer ensuite sur ANIMATION 
pour lancer
l'animation
*Régler le nombre de pas à 12 :
*Pour suivre l'évolution du mouvement pas à pas , cliquer sur :
(s'assurer qu'uncune des cases à cocher n'est cochée :
*Click FIN ANIMATION 
c)Trajectoire relative :
Nous allons nous interesser à présent à la trajectoire de la boule par rapport à la bicyclette.
Mathématiquement cela revient à construire la courbe Dy = y1-y2 en fonction de Dx= x1-x2 .
*Activer la fenêtre GRANDEURS en cliquant sur l'icône (en haut à
gauche) 
Click CREER GRANDEUR 
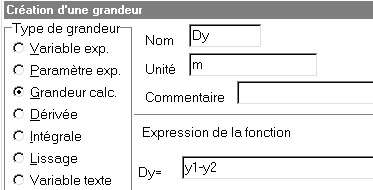
*Compléter la fenêtre comme indiqué ci-contre :
*Ok
*Créer ensuite en procédant de la même façon Dx=x1-x2
*
Reste à visualiser la courbe Dy=f(Dx)
*Activer la fenêtre GRAPHE 
*Click COORDONNEES 
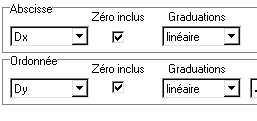
*Ajouter 
*Mettre à jour la fenêtre :
* Ok
Q3)Représentez sur votre copie les trois trajectoires . Désigner :
*celle qui correspond au mouvement de la boule par rapport au sol .
*celle qui correspond à la trajectoire de l'axe de la roue avant de la bicyclette par rapport au sol .
*celle qui correspond à la trajectoire de la boule par rapport à la bicyclette . Quelle est la nature de chacune des trajectoires ? Conclure
Quitter Regressi (Fichier/Quitter) . Fermer également les autres fenêtres sans sauver les fichiers.
IV/Trajectoire de Mars :
Nous venons de constater que la trajectoire d'un point mobile dépend du référentiel . Nous allons nous interesser à présent à la trajectoire de la planète Mars dans deux cas :
* Le référentiel est le soleil
* Le référentiel est la terre .
*Ouvrir le dossier LOGICIELS (double-click)
*Lancer le programme ASTRO (double-click)
*Appuyer sur F1 : Modèles Hélio <> geo Soleil Terre Mars
*Année de départ : 2002
*Année finale : 2003
*choix du mode : 2 (mode manuel)
*Appuyer ensuite sur la barre Espace (en bas du clavier)
Observer les trajectoires qui se dessinent à l'écran .
Q4)Représentez les schémas sur votre copie . Lequel correspond à la trajectoire de Mars par rapport à la terre ?
Appuyer sur la touche "Echap" du clavier pour sortir et sur F10 pour terminer .
CORRECTION :
1)
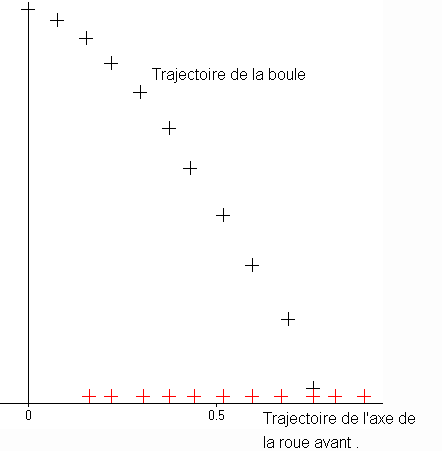
2)La boule a une trajectoire parabolique
La trajectoire de l'axe de la roue est une droite .
3)
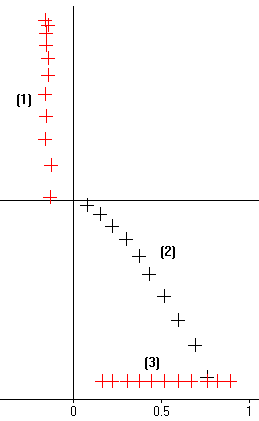
(1) : Dy = f(Dx) : trajectoire de la boule par rapport à la bicyclette . C'est une droite
(2) : trajectoire de la boule par rapport au sol . C'est une parabole .
(3) : trajectoire de l'axe de la roue par rapport au sol .
Pour les courbes (1) et (2) , il s'agit de la trajectoire de la boule dans des référentiels différents . Ces deux courbes sont différentes , autrement dit , la trajectoire d'un "objet " dépend du référentiel .
4)
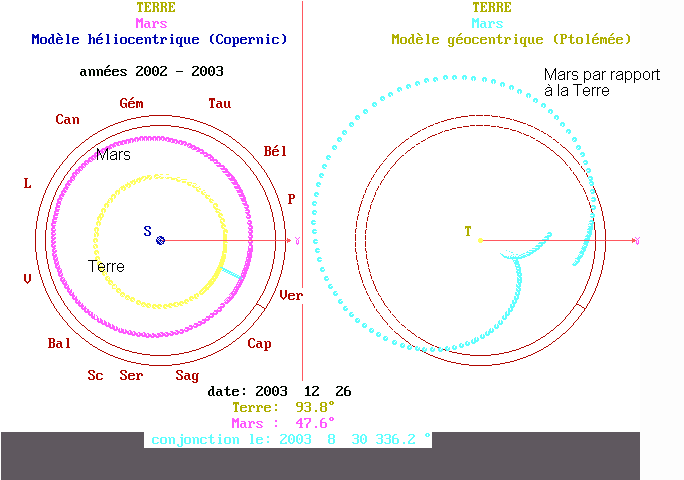
La fenêtre de gauche montre les trajectoires de la Terre et de Mars par rapport au référentiel .
La fenêtre de droite montre la trajectoire de Mars par rapport à la terre . Il est évident que ces deux trajectoires sont différentes : nous constatons là encore que la trajectoire dépend du référentiel .