TP P5 : CHUTE LIBRE
I/But du TP
Il s'agit de mettre en évidence les lois de chute libre en déterminant :
* l'équation horaire x(t)
* la loi de vitesse v(t)
II/Le dispositif
Le dispositif d'acquisition est constitué d'une diode qui envoie un faisceau lumineux vers une cellule réceptrice . On dispose d'une règle , constituée d'une succession de bandes transparentes et opaques .
On abandonne la règle en chute libre perpendiculairement au faisceau lumineux . Le dispositif permet ainsi de suivre le déplacement "x" de la règle en fonction du temps.
III/Acquisitions
*Relier la fiche DIN du dispositif d'acquisition à la fiche A de l'interface Orphy
*Mettre l'interface en marche
*Lancer le logiciel CHUTELIB (dans document LOGICIELS en C25).
Déroulement d'une d'acquisition :
*click souris MESURE - un message apparait "FAIRE LA MESURE"
*tenir la règle suspendue au-dessus du faisceau , perpendiculairement à celui-ci , par le fil fixé à la règle .
*lâcher le fil (la règle est alors abandonnée en chute libre)
*lorsque l'acquisition est terminée , cliquer Ok ; Le message " Je trie les mesures " apparaît alors ... Patientez . En fin de traitement le message s'efface .
Losque le tri des mesures est terminé :
*click souris REGRESSI (le logiciel Regressi , tableur- grapheur est alors chargé en mémoire). Les valeurs obtenues au cours de l'acquisition sont alors transférées automatiquement vers Regressi .
*Revenir à CHUTLIB en cliquant sur le coin supérieur droit de la fenêtre de Regressi :
*Refaire une nouvelle acquisition (voir ci-dessus)
*Click souris REGRESSI . A la question qui suit : " Nouvelle page ?" , cliquer OUI
*Revenir ensuite à CHUTELIB (voir ci-dessus) .........
Faire en tout 4 acquisitions (pages 1 à 4 )
IV/Traitement des données (avec Regressi)
revenir à la page 1 en utilisant la souris 
a)Equation horaire
*activer la fenêtre graphique si elle ne l'est pas déjà 
Q1)A quel type de courbe correspond à priori l'équation horaire x(t) ?
*modélisation
-De la fenêtre GRAPHE , cliquer sur l'icône Modélisation
-Dans la fenêtre Expression du modèle , taper x=0.5*a*t*t+b*t+c (modèle parabolique)
-cliquer sur le bouton Ajuster : le logiciel donne les différents paramètres a, b et c
Q2)Reporter dans le tableau les différentes valeurs numériques de a pour chacune des pages : (à chaque page cliquer sur le bouton AJUSTER )
page 1 |
page 2 |
page 3 |
page 4 |
|
a |
||||
b |
Quelle est l'unité de a ?Comparer la valeur du paramètre a à la norme du champ de pesanteur . Conclure .
b)la vitesse
Etant données deux positions successives de l'extrêmité "avant" de la règle à deux instants t1 et t2 , x1 et x2 étant les abscisses correspondants , la vitesse moyenne de la règle entre les instants t1 et t2 est donnée par l'expression :
On peut admettre , si l'intervalle t2-t1 est suffisamment petit , que cette grandeur représente bien la vitesse instantanée de la règle à un instant t compris entre t1 et t2
Autrement dit :
Comme cela sera vu en mathématiques, la définition de V(t) n'est autre que la dérivée de x(t) par rapport à l'instant t .
Le logiciel permet de calculer V(t)
*cliquer sur l'icône Fin de modélisation
*Rendre active la fenêtre Grandeurs
*Cliquer sur l'icône : Creer une grandeur 
*Compléter la fenêtre comme indiqué ci-dessous:
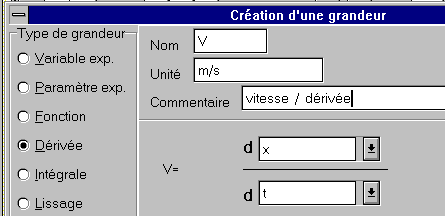
Vous constatez que la dérivée est notée 
.
C'est la notation qu'utilisent les physiciens pour dire que V est la dérivée de x par
rapport au temps .
Remarque sur l'unité de V :Tenant compte des unités qui ont été retenues lors de l'acquisition , t en ms et x en mm , V s'exprime alors en mm.ms-1 . On remarquera que cette unité est identique à des m.s-1 .
*Cliquer Ok et Mise à jour
*Revenir à la fenêtre graphe
*Cliquer sur l'icône COORDONNEES et choisir V comme ordonnée au lieu de x ; Ok
*Modéliser en proposant pour V(t) une expression de la forme : V(t) = p*t+q
*Click AJUSTER
Q3)Comparer a et p , b et q pour chacune des pages . Conclure
c)Interprétation des différents paramètres
Q4)Quelles sont les unités de a , b et c si on exprime x en mètres et V en mètres par seconde . Donnez une interprétation physique simple de b et c .
d)Mouvement de chute libre sans vitesse initiale
Si nous choisissons l'origine du repère telle qu'à t=0 on ait x=0 , l'équation horaire du mouvement de chute libre sans vitesse initiale s'écrit :
Q5)Posons c = x0 , b=V0 . Montrer que :
V/Exercice complémentaire :
On étudie la chute libre d'une bille d'acier dans l'air à l'aide du dispositif schématisé ci-dessous . La bille est initialement maintenue par un électro-aimant.
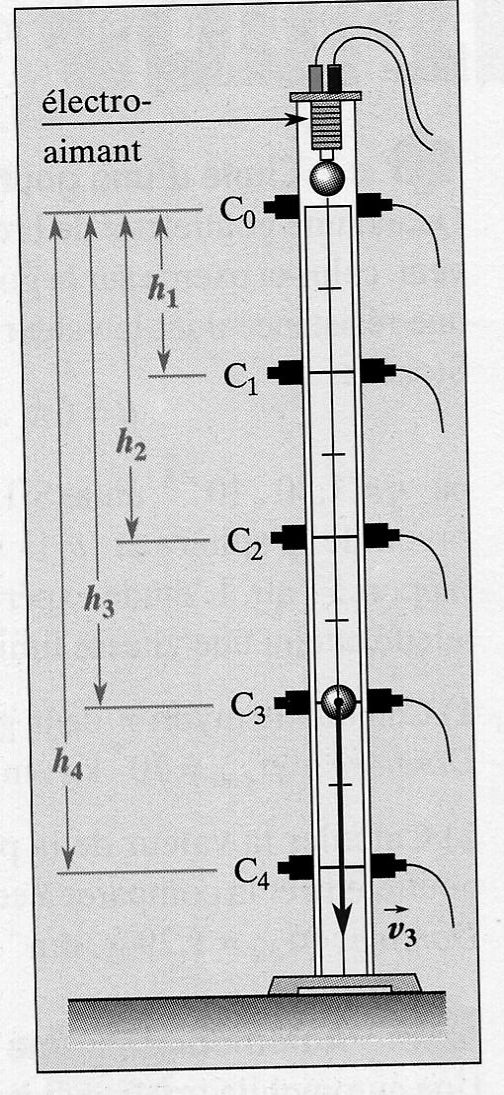
On dispose d'une règle verticale équipée de photocapteurs distants de L .
L'appareil mesure la durée Dt mise par la bille pour passer devant chaque cellule . Ces capteurs sont reliés à un ordinateur qui calcule la vitesse v pour une hauteur de chute h .
On a relevé le tableau de mesures suivant :
h (cm) |
20 |
40 |
60 |
80 |
v (m.s-1) |
1,980 |
2,803 |
3,433 |
3,964 |
h (cm) |
100 |
120 |
140 |
v (m.s -1) |
4,432 |
4,848 |
5,238 |
a)Tracer le graphe v2 en fonction de h
b)La loi de chute libre est-elle vérifiée ? Si oui , en déduire une valeur moyenne de g
c)Quelles sont les forces , exercées sur la bille , qui apparaissent négligeables au cours de cette chute ?
