TP P2 : Mouvement du centre d'inertie
I/Objectifs :
*Mettre en évidence le caractère particulier du mouvement du centre d'inertie d'un solide .
*Construire des vecteurs vitesse
*Mettre en évidence le caractère relatif du mouvement .
II/Trajectoire du centre d'inertie :
a)Centre d'inertie d'un disque
Un disque en plexiglas est lancé sur une table soufflante horizontale . Le souffle d'air permet de limiter les frottements entre le disque et la table .
Il apparaît que le centre du disque a un mouvement plus simple que les autres : un mouvement rectiligne uniforme . Ce point est le centre d'inertie du disque .
b)Centre d'inertie d'un solide constitué de deux solides de centres d'inertie G
1 et G2Etant donné un solide S constitué de deux solides S
1 et S2 de centres d'inertie G1 et G2 et de masses m1 et m2 , on peut montrer que le centre d'inertie G du solide S est le barycentre de G1 et G2 affectés des coefficients m1 et m2 , c'est à dire que :Q1)Montrer que la relation précédente permet de montrer que :
*G appartient au segment G
1G2*![]()
c)Construction de la trajectoire du centre d'inertie de S :
Le solide S est constitué de deux mobiles autoporteurs cylindriques . Chaque mobile (S1 ou S2) est équipé au centre , dans sa partie inférieure d'une pointe , qui permet d'enregistrer la position du centre d'inertie du mobile (le papier est "brulé" par des décharges électriques) à intervalles de temps égaux .
Le solide S est lancé sur la table et les trajectoires des centres d'inertie G
1 de S1 et G2 de S2 sont enregistrées . Le document joint est un exemple d'enregistrement .Celui-ci a été établi sur une table horizontale .Q2)Sur chacun des documents nommez les différentes positions des deux centres d'inertieA
0, A1 ,A2 ....(pour G1). , B0 ,B1,B2 ...(pour G2).Q3)En utilisant deux couleurs différentes , tracer les trajectoires de G
1 et G2 sur chacun des deux documents .Q4)Les deux mobiles ont la même masse .Construire les positions successives de G, centre d'inertie de l'ensemble : C
0 , C1 , C2 .......III/Exploitation du document
Q5)Tracer la trajectoire de G sur le document . Quelle est la nature de cette trajectoire ? Le centre d'inertie de S a t-il un mouvement rectiligne ?
Q6)La durée entre deux pointages est égale à
t =60 ms .Quelle est la durée de l'enregistrement (entre le premier point et le dernier ) ?Q7)Calculer la vitesse moyenne du centre d'inertie ![]() , où t
, où t
Q8)Un mouvement est uniforme si la vitesse est constante au cours du temps . Le mouvement de G est-il uniforme ? Justifiez clairement votre réponse .
Q9)Enoncez le principe d'inertie .Le mouvement du centre d'inertie G du système S vérifie t-il le principe d'inertie ?Le système est-il pseudo-isolé ? Justifiez clairement cette dernière réponse .
IV/ Vecteur vitesse :
a)Vitesse moyenne et vitesse instantanée :
Une vitesse moyenne est égale au rapport de la distance parcourue sur la durée pendant laquelle est parcourue cette distance .
Comment mesurer une vitesse instantanée si on ne dispose pas de tachymètre ?
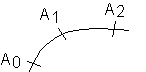
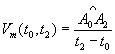 est la vitesse moyenne
entre t0 et t2.
est la vitesse moyenne
entre t0 et t2.
![]() est la distance mesurée sur la
trajectoire.
est la distance mesurée sur la
trajectoire.
Si l'intervalle de temps t
2-t0 est suffisamment petit , nous admettrons que la vitesse instantanée en t1 : V(t1) est telle que V(t1) = Vm(t0,t2) . En général , on peut dans ce cas confondre la mesure du segment A0A2 et la mesure de l'arc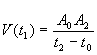
Q10)A partir du document , déterminer en cm.s
-1 la vitesse instantanée du centre d'inertie G du solide S aux instants t2 et t12 .Ce résultat est-il en accord avec votre réponse à la question Q8 ? .b)Vecteur vitesse :

Il peut être intéressant de construire un vecteur vitesse instantanée tel que :
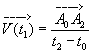
Ce vecteur a la direction du segment A
0A2 , le sens du mouvement (point se déplaçant de A0 vers A2 ) et a pour norme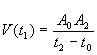 , ce qui la vitesse instantanée à l'instant t1 .
, ce qui la vitesse instantanée à l'instant t1 .
Pour construire ce vecteur :
*on trace le segment A
0A2*on trace une demi-droite dont l'origine est en A
1 et qui est parallèle au segment A0A2 .*on choisit une échelle des vitesses . Choisissons par exemple d'associer à 1 cm.s
-1 ------> 0,12 cm :Pour V(t1) = 20 cm.s-1 , le vecteur vitesseQ11)Sur le document , construire les vecteurs vitesse du centre d'inertie G aux instants t
2 et t12 en choisissant une échelle adaptée , que l'on précisera (On présentera clairement le détail des calculs sur la copie).. Le vecteur vitesse de G est-il constant au cours du mouvement ?V/Caractère relatif du mouvement :
a)Protocole :
En utilisant le document :
1-Sur une feuille de papier calque , tracer deux axes orthogonaux en plaçant l'origine au centre de la feuille .
Soit O' l'origine commune de ces axes .
2-Faire coincider O' et A0 . S'assurer que les axes de la feuille de calque et du document (enregistrement) sont bien parallèles deux à deux .
3-Par transparence , porter C0 sur le papier calque .
4-Faire coïncider O' et A1 ............
Répéter les mêmes opérations qu'en (2) et (3) et reporter C1 sur le calque .
Ce protocole nous permet de construire la trajectoire de G par rapport à un repère R' centré en G
1 .b)Trajectoire de G par rapport à G
1 :
Q12) Quelle est la nature de la trajectoire de G par rapport à G
1 ? Le mouvement de G dans le nouveau repère R' centré en O' (O' est confondu à tout instant avec G1) est-il uniforme ?Q13)Comparer les mouvements de G par rapport au repère R' et par rapport à un repère terrestre .
c)Vitesse angulaire :

Etant donné un point M qui décrit une trajectoire circulaire:
![]()
est la vitesse angulaire de M à l'instant t2
Q14)Si
q est exprimé en degrés et t en secondes , quelle est l'unité de w ? Q15) On s'interresse au mouvement de G dans le repère R' . Déterminer la vitesse angulaire de G aux instants t2 et t7 . ConclureCORRECTION :
1)La relation barycentrique peut aussi s'écrire : ![]() d'où :
d'où :
![]() , soit finalement lorsqu'on passe aux normes :
, soit finalement lorsqu'on passe aux normes :
![]() c.q.f.d.
c.q.f.d.
TELECHARGER LE DOCUMENT COMPLETE
2)voir document
3)voir document
4)Comme les masses des deux mobiles sont identiques, GG1=G1G2/2 , autrement dit , C0 est le milieu de A0B0, C1 est le milieu de A1B1 …………..
5)La trajectoire de G est une droite , autrement dit le centre d'inertie de S a un mouvement rectiligne .
6)Entre C0 et C15 il y a 15 intervalles de 60 ms : t15-t0= 15*60 = 900 ms .
7)C0C15 = 17 cm et donc Vm= 17 cm / 0,9 s = 18,5 cm.s-1 .
8)Le mouvement de G est bien uniforme . L'intervalle entre deux pointages successifs est toujours le même (C0C1=C1C2=C2C3………) et comme l'intervalle de temps entre deux pointages est toujours le même aussi (60 ms) , la vitese de G est constante . G a par conséquent un mouvement uniforme .
9)Le centre d'inertie d'un système persiste dans sont état de repos ou
de mouvent rectiligne uniforme lorsque le système est isolé ou pseudo- isolé .Or ici ,
le système constitué des deux mobiles est bien pseudo isolé lorsque la table est
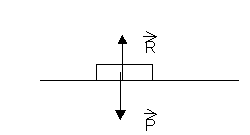
horizontale et en l'absence de frottements puisque le poids ![]() de l'ensemble et l'action de la table sur les mobiles se
comprensent (
de l'ensemble et l'action de la table sur les mobiles se
comprensent (![]() ):
):
10)![]() ;
; ![]()
Ce résultat est bien en accord avec la réponse à la question Q8 (vitesse constante)
11)Choisissons l'échelle de vitesse : 20 cm.s-1 ------->2,5 cm .
Les deux vecteurs ![]() seront représentés par une
flèche de 19,1/20*2,5 = 2,3 cm de longueur (voir document) .Ces deux vecteurs sont égaux
(même direction , même sens , même norme).
seront représentés par une
flèche de 19,1/20*2,5 = 2,3 cm de longueur (voir document) .Ces deux vecteurs sont égaux
(même direction , même sens , même norme).
12)G décrit un cercle par rapport à un repère centré sur G1 .La distance entre deux points successifs étant constante (la durée entre deux pointages succesifs est constante), nous en déduisons que le mouvement de G dans le nouveau repère R' est uniforme .
TELECHARGER LA TRAJECTOIRE DE G PAR RAPPORT A R'
13)les trajectoires de G dépendent du repère : ce ne sont pas les mêmes dans les deux repères .
14)w s'exprime en rad.s-1 .
15)w(t2)=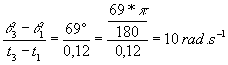 (q3-q1 peut être
mesuré avec un rapporteur). Nous avons q13-q11=69° et donc w(t2)=w(t12)=10 rad.s-1. Ce résultat est tout à
fait en accord avec ce qui précède puisque G a un mouvement uniforme .
(q3-q1 peut être
mesuré avec un rapporteur). Nous avons q13-q11=69° et donc w(t2)=w(t12)=10 rad.s-1. Ce résultat est tout à
fait en accord avec ce qui précède puisque G a un mouvement uniforme .