I/L'énergie cinétique
a)D'une masse ponctuelle m :
b)D'un solide de masse M en translation
Rappel :Tous les points du solide ont à un instant donné (quelque soit cet instant considéré) le même vecteur vitesse .
c)D'un solide en rotation autour d'un axe fixe D
: JD
est appelé "Moment d'inertie" du solide par rapport à l'axe D (en Kg.m2 )
w est la vitesse angulaire du solide à l'instant considéré (en rad.s-1 ) .
II/Energie potentielle :
L'énergie potentielle résulte de l'interaction entre différentes parties d'un système ou entre différents sytèmes .
a)Energie potentielle de pesanteur :
*Système : masse {m} dans le champ de pesanteur
*Force d'interaction : le poids 
Ep=mgz pour une masse ponctuelle
Ep = mgzG pour un solide
L'énergie potentielle de pesanteur est la conséquence de l'association :
On dit que le poids dérive d'un potentiel .
Remarque :Ep dépend de la définition d'un état de référence (état pour lequel l'énergie potentielle est nulle) . La différence d'énergie potentielle entre deux états est par contre indépendante de l'état de référence .
b)Energie potentielle élastique
Système : masse {m} soumise à l'action du ressort (tension 
)
Force d'interaction : la tension (T=k DL avec DL allongement ou réduction de la longueur du
ressort par rapport à sa position de repos)
k est la constante de raideur du ressort (voir chap Systèmes élastiques)
L'énergie potentielle élastique est la conséquence de l'association :
III/Travail d'une force :
a)Rappel :
Le travail est un mode d'échange ordonné d'énergie .
b)Travail d'une force constante :
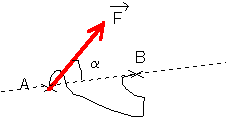
Soit 
une force
constante , dont le point d'application passe de A à B , selon une trajectoire quelconque
:
est le travail de la
force lorsque son point d'application
passe de A à B (a est l'angle tel
que
.
c)Cas particuliers :
* 
est perpendiculaire à 
: =0
Une force perpendiculaire au vecteur déplacement de son point d'application ne travaille pas .
* et ont la même direction et le même sens : = F. (AB)
* et ont la même direction et sont de sens opposés := - F.(AB)
d)Décomposition d'une force :
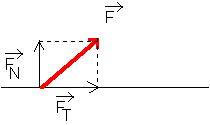
La force est telle que 
a la direction de la tangente à la
trajectoire du point f'application de .
Autrement dit :
est la composante
tangentielle de
est la composante normale de
Alors : 
IV/Conservation de l'énergie mécanique :
a)Energie mécanique :
Pour un système S : E=Ep + Ec .
E est l'énergie du système mécanique S
b)Conditions de conservation :
S'il n'y a pas d'autres forces que celles dont l'énergie potentielle associée est EP pour réaliser un transfert d'énergie par travail mécanique, alors :
L'énergie mécanique du système S est constante .
Un tel système est conservatif (E=cste)
c)Exemples :
* chute libre (voir TP)
* solide en mouvement sur un plan incliné , sans frottement :
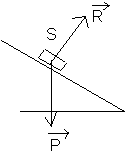
Système : {solide}
Forces :
: travaille . Energie
potentielle Ep
: ne travaille pas
Le {solide} en mouvement sur le plan incliné , dans le champ de pesanteur est un système conservatif . (car nous sommes dans les conditions d'application définies au paragraphe précédent)
c)Conséquences :
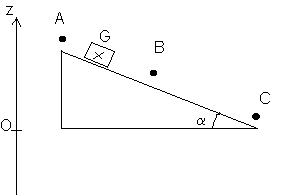
Nous reprenons l'exemple précédent du mouvement d'un solide S sur un plan incliné , sans frottement :
E=Ep + Ec = mgz + 1/2 mV2
Ci-dessous sont représentées les grandeurs E
p , E et Ec en fonction de z
|
|
|
Ci-dessous sont représentées sous forme de bâtons les différentes formes d'énergie lorsque le solide passe de A à B .
Il apparaît que :
* l'énergie mécanique est constante (système conservatif)
* Au cours du mouvement du solide , il y a échange entre l'énergie potentielle et l'énergie cinétique .
en A : E = E
p(A) = mgzA puisque l'énergie cinétique est nulle .en un point M quelconque (non représenté sur les schémas) : E = E
M= 1/2 mV2 + mgzLe système étant conservatif , nous pouvons écrire E=E
A=EM ou :mgz
A = 1/2 mV2 + mgz et doncNous pouvons par ailleurs mlontrer que z-z
A = L sin a où L =AM (distance parcourue par le centre d'inertie du solide entre A et M)et par conséquent :
V
2=2gL sin aV/Systèmes non conservatifs
a)Dans quel cas ?
Lorsqu'il y a des forces qui travaillent et qui ne dérivent pas d'un potentiel , l'énergie mécanique n'est pas conservée , c'est à dire que le système n'est pas conservatif .
Exemple : lorsqu'il y a des forces de frottement .
b)Variation d'énergie mécanique :
Etant donné un système mécanique S . Celui-ci peut être soumis à deux types de forces :
1-celles qui dérivent d'un potentiel (exemple : le poids)
2-celles qui ne dérivent pas d'un potentiel (exemple : force de frottement)
Nous admettrons le résultat suivant :
La variation d'énergie mécanique est égale au travail des forces qui ne dérivent pas d'un potentiel
c)Résolution d'un exercice :
Enoncé: La piste de descente olympique << La face de Bellevarde>>, à Val d'Isère, est longue de 3000 m et présente une dénivelée de 900 m entre le point de départ et le point d'arrivée .
1)Calculer l'énergie potentielle du skieur dans le champ de pesanteur au départ de la piste et à l'arrivée (masse du skieur équipé m=80 kg)
2)Calculer l'énergie mécanique du système {skieur} dans le champ de pesanteur au départ et à l'arrivée en supposant que les frottements sont négligeables.
3)Quelle serait alors la vitesse atteinte par le skieur au bas de la piste ?
4)En ralité , la vitesse maximale mesurée est de 140 km.h-1 .Quelle conclusion peut-on en tirer ? Calculer la variation d'énergie mécanique du skieur .
1-Ep(A) = mgzA où A est le point de départ . AN : Ep(A) =80x10x900= 720.103 J
Ep(C)=mgzC où C est le point d'arrivée . Ep(C)= 0 J (zC=0)
2-Les forces apliquées sont -le poids du kieur équipé : dérive d'un potentiel
- l'action du sol sur le skieur (sans frottement) : ne travaille pas
Le système est donc conservatif : E(A)=E(C)
avec E(A)=Ep(A) puisque l'énergie cinétique au départ est nulle .
finalement E(A)=E(C)=720.103 J
3-En C : E(C)=E=Ep(C)+Ec(C) =Ec(C) puisque Ep(C)=0
et donc 1/2 mVC2 = E d'où 
; AN Vc= 134 m/s = 483 km.h-1
4-La vitesse est en réalité égale à 140 km.h
-1 , donc très inférieure à la valeur précedemment calculée : les frottements ne peuvent donc pas être négligés .E(A)-E(C) = (E
p(A)-Ep(C))+(Ec(A)-Ec(C))AN : E(A)-E(C) = 720.10
3 - 0,5x80x(140000/3600)2 = 660.103 Jet comme 
, nous en déduisons que le travail
des forces de frottement lorsque le skieur descend la pente, est égal à - 660.10
VI/Exercices :
1- n°7 page 175
question 1-a : système : mobile sur la table inclinée dans le champ de pesanteur
question 2-a : le système est-il soumis à des forces non conservatives (ou qui ne dérivent pas d'un potentiel ) ?
2-n°
s 12 et 13 page 1763-n°15 page 176
4-n° 21 page 177
système : eau dans le champ de pesanteur .
5-n° 28 page 178
système : sphère dans le champ de pesanteur .
VII/Exercices complémentaires
Exercice 1 : oscillations d'un pendule
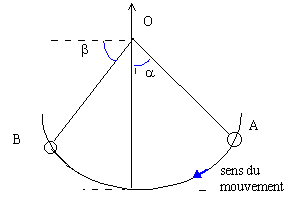
Les frottements sont négligeables. Un bille de masse m est suspendue à un fil de masse négligeable. L'origine de l'énergie potentielle de pesanteur est le point le plus bas.
m=200 g; OA=0,5 m ;
a=0,6rad ; b=1 rad.vitesse initiale en A : 7,2 km h
-1.1 m s
-1 =3,6 km h-1.-1.a)Calculer les altitudes de A et B
b)Calculer l'énergie mécanique en A
c)Calculer la vitesse en B en km h
d)la masse de la bille double, que deviennent
· l'énergie mécanique ? · la vitesse en B ?
Exercice 2 :plan incliné au sommet arrondi
Les frottements négligeables. Un bille de masse m lancée de A à la vitesse V se déplace vers D. L'origine de l'énergie potentielle de pesanteur est le point le plus bas A.
m=1 kg; OB=0,5 m ;AB=2 m ;
a=0,3rad ; b=0,9 rad.vitesse initiale en A : 18 km h
-1. (1 m s-1 =3,6 km h-1).
-1.a)Calculer les altitudes de B , C et D.
b)Calculer l'énergie mécanique en A
c)Calculer la vitesse en D en km h
d)la vitesse initiale est divisée par deux, que deviennent
· l'énergie mécanique ? · la vitesse en C et en D ?
Exercice 3 :descente d'une piste
Les frottements sont négligeables. Un bille de masse m lancée de A à la vitesse V se déplace vers M. L'origine de l'énergie potentielle de pesanteur est le point le plus bas O. Le solide décolle après être passé en M.
m=1 kg; OB=0,8 m ;AB=2 m ;
a=0,1 rad ; b=1,06 rad.vitesse initiale en A : 3,6 km h
-1.-1.a)Calculer les altitudes de A , B et M.
b)Calculer l'énergie mécanique en A
c)Calculer la vitesse en M en km h
d)la vitesse initiale est nulle, que deviennent
· l'énergie mécanique ? · la vitesse en B ?
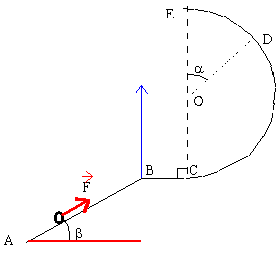
Exercice 4 : bille sur une glissière
Les frottements sont négligeables. Un bille de masse m lancée de A à la vitesse V se déplace vers D. L'origine de l'énergie potentielle de pesanteur est le point A. Une force constante de valeur F=2 N agit entre A et B; l'énergie mécanique en A augmente de F*AB sur le trajet AB.
m=100 g; OD=1 m ;AB=2 m ;
a=0,5 rad ; b=0,2 rad.vitesse initiale en A : 7,2 km h
-1.-1.a)Calculer les altitudes de B et D.
b)Calculer l'énergie mécanique en A et en B
c)Calculer la vitesse en C puis en D en km h
d)la valeur de F est 0,5 N, que deviennent
· l'énergie mécanique ? · la vitesse en B et D ?
Exercice 5 : Le grand huit
Un wagonnet de <<grand huit>> d'une fête foraine, chargé de ses occupants, et de masse totale M=650 kg , passe le point A de la piste avec une vitesse V
A . La portion de piste considérée est représentée ci-contre . Le niveau de référence choisi est celui du point B .
1/On suppose d'abord les forces de frottement et la résistance de l'air négligeables.
a)Quelle doit être la vitesse V
A du wagonnet en A pour qu'il puisse atteindre le sommet D ?b)Calculer alors la vitesse V
B du wagonnet en B .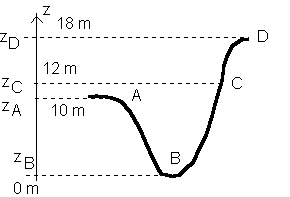
2/En réalité , les forces de frottement et la résistance de l'air ne sont pas négligeables. Avec la vitesse V
A calculée précedemment le wagonnet ne parvient qu'au point C de la piste .a)Calculer le travail W
f des forces de frottement et de la résistance de l'air sur la portion AC.b)Le rapport 
représente le travail des forces de résistance au mouvement par mètre de dénivellation
parcouru. On suppose que la valeur de ce rapport est la même pour tout le parcours AD.
Calculer le travail que doit fournir un moteur annexe pour que le wagonnet puisse atteindre D à faible vitesse .
Exercice 6 : Ressorts
Un mobile autoporteur de masse m=0,612 kg de centre d'inertie G, peut se déplacer sur une table plane et horizontale . Il est accroché à deux ressorts R
1 et R2 identiques, de même constante de raideur k=4,96 N.m-1 , de masses négligeables devant m , tendus entre deux points fixes C1 et C2 . Sa position est repérée par l'abscisse x de son centre d'inertie, comptée à partir de sa position d'équilibre. A l'équilibre du mobile , les ressorts ne sont ni étirés , ni comprimés .Le mobile est écarté de sa position d'équilibre dans la direction C
1C2, puis abandonné sans vitesse initiale . Ses positions sont relevées à intervalles de temps égaux de durée q = 60 ms, sur une feuille de papier déplacée horizontalement à vitesse constante dans une direction orthogonale à C1C2 (fig. suivante).
1/Si l'un des ressorts était utilisé seul pour suspendre le mobile, quel serait son allongement à l'équilibre ?
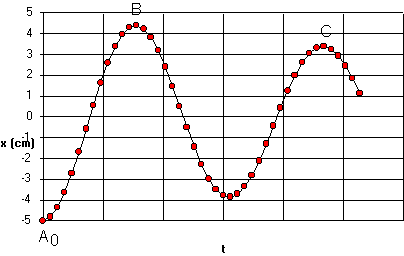
2/Evaluer la "période" (plus exactement pseudo-période dans le cas présent) du mouvement enregistré .
3/Calculer en B , puis en C l'énergie potentielle élastique du système {ressorts-mobile}. On admettra qu'elle est donnée par l'expression E
p = k.x2 .4/Calculer le travail des forces de frottement pour une durée égale à une période .
Exercice 7: Déterminer une force de frottement
Le Erreur! Signet non défini.fil est inextensible et sans masse. La poulie tourne sans frottement et sa masse est négligeable. S' chute d'une hauteur h et S glisse d'une distance d avant de s'arrêter. La vitesse au départ nulle.
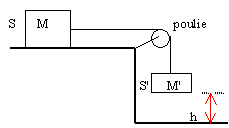
Les frottements sont supposés constants sur le plan horizontal.
a)Ecrire le th. de l'énergie cinétique pour le système {S , fil et S'}.
b)Exprimer la valeur de la force de frottement f en fonction de M, M',d ,h, g
c)Calculer f si M=1 kg; M'=5 kg; h=0,1 m; d=0,3 m;
d)Calculer la vitese maximale atteinte.
