
Chap P7 :Correction des exercices :
Exercice 2 page 159 :
imA,com est négative : cela signifie que le sens conventionnel du courant entre mA et com ,va de com vers mA , autrement dit de N vers M (imA,com = iMN )

Exercice 3 page 159 :
1) Le voltmètre mesure UBA = UV,com
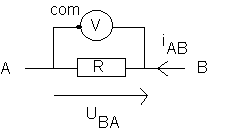
2)La loi d'ohm appliquée au conducteur ohmique , s'écrit ici : UBA = R iBA et donc iBA = 1,32/100 = 13,2 10-3 A = 13,2 mA .
L'intensitée algébrique iBA étant positive , on en déduit que le courant (sens conventionnel) va de B vers A .
Exercice 6 page 159 :
a)puissance électrique reçue : P=UI = 1,5*0,65= 0,97 W , ce qui correspond approximativement à 1 W .
b)Energie : E = P*Dt = 1*2*60 = 120 J
Exercice 12 page 160 :
P=UI et U=RI : en combinant les deux formules nous obtenons P=U2/R et donc R= U2/P = (48)2/1800 = 1,28 W .
I=U/R = 48/1,28= 37,5 A
Exercice 15 page 160 :

P=UI et U=RI : en combinant les deux formules , nous obtenons :P=RI2 . L'énergie thermique correspondante libérée par effet Joule est EJ = P*Dt = RI2Dt . Si on double le courant , l'énergie libérée pendant l'intervalle de temps Dt' est E'J = 4RI2Dt' . Il est clair que les deux énergie sont égales (Ej = E'J ) si 4 Dt' = Dt ou Dt' = Dt/4 = (21*60+12)/4 = 318 s = 5 mn 18 s .
Exercice 17 page 160
1)

Ee =UI(Dt) : énergie électrique reçue par le moteur .
Ee = 4,5*0,75*60 = 202 J
2)EJ= P * Dt = rI2 * Dt = 0,85*0,752 * 60 = 28,5 J
Ee=EJ + EM où EM correspond à l'énergie mécanique fournie par le moteur . EM = Ee- Ej= 173,5 J
Or EM = PM Dt = E'I Dt et par conséquent E'= EM/IDt= 3,8 V .
Exercice 22 page 160 :
1)UPN = E - rI : On trace la fonction UPN = f(I) : c'est une fonction affine d'ordonnée à l'origine E= 22 V et de coefficient directeur - r (pente négative) :
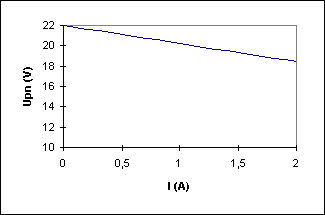
2)PJ = rI2 = 1,78*22 = 7,12 W
P = EI - Pj = 22*2-7,12= 36,8 W
Exercice 23 page 161 :
1)
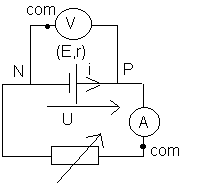
Les appareils sont branchés de façon à donner des mesures positives .
2)
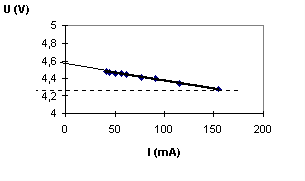
3)U=f(I) est une fonction affine de la forme U= (-r) I + E .
L'ordonnée à l'origine se lit directement sur la courbe : E= 4,6 V
Le coefficient directeur est négatif est égal à -r = (4,25 - 4,6)/(0,155-0) = -0,0023 d'où la résistance interne r= 2,3 W (attention aux unités !).
Schéma équivalent :
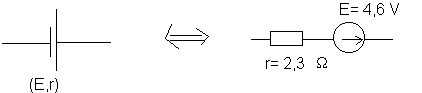
4)-a : I= (E-U)/r= (4,6 - 4,24)/2,3= 0,156 A = 156 mA ; P=UI = 4,24*0,156 = 0,66 W
b : Weg = P*Dt = 20 J
c : Ej = rI2 Dt = 2,3* (0,156)2 * 30 = 1,68 J
d: Ech = EI Dt = 4,6 * 0,156 * 30 = 21,6 J
Exercice 24 page 161 :
1)L'équation-bilan est bien équilibrée .
2)Lorsque l'accumulateur est utilisé en générateur , c'est la réaction inverse qui se produit .
Exercice 1 page 176 :
On se reportera au livre pages 170 et 171 pour la démonstration des résultats suivants :
* Deux résistances R1 et R2 , branchées en série sont équivalentes à une résistance unique R=R1+R2 .
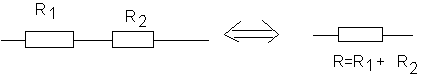
* Deux résistances R1 (de conductance G1 = 1/R1 ) et R2 branchées en parallèle sont équivalentes à une résistance unique R de conductance G=1/R , telle que G=G1+G2 .
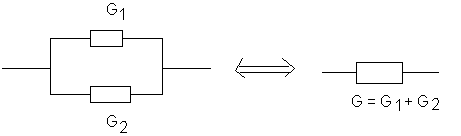
Pour obtenir une résistance de 500 W il faut associer à la résistance de 330 W , une résistance de 170 W en série .
Exercice 2 page 176 :
R1 = 1500 W et donc G1=1/R1 = 6,6 10-4 S = 0,66 mS
R2= 3000 W et G2 = 3,3 10-4 S = 0,33 mS
Si les deux résistances sont branchées en parallèle G=G1+G2 = 1 mS R= 1000 W .
Il est clair que R est inférieure à la plus petite des deux résistances et que G est supérieure à la plus grande des deux conductances .
Exercice 6 page 176 :
* L'association en parallèle de la résistance de 20 W et de la résistance de 40 W est équivalente à une résistance unique R telle que 1/R = 1/20 + 1/40 = 3/40 W-1 , d'où R= 40/3= 13,3 W .
* Cette résistance associée en série avec l'autre de 20 W est équivalente à une résistance unique de 33,3 W .
Vu de la pile , le circuit est donc équivalent à :
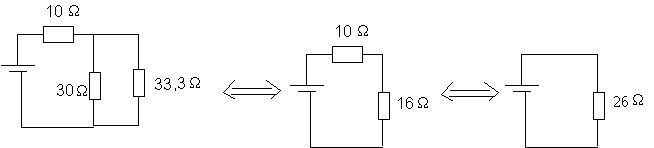
Le dipôle connecté à la pile est donc équivalent à une résistance de 26
W .
Exercice 10 page 176 :
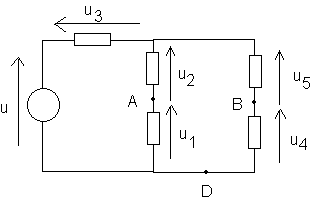
Nous avons : u=u1+u2+u3 et donc u2= u-u1-u3 = 9-4,5-3,6 = 0,9 V
u= u4+u5+u3 et donc u4 = u-u3-u5 = 9-1,8-3,6 = 3,6 V
uAB = u1-u4 = 4,5 - 3,6= 0,9 V
uBD = u4 = 3,6 V
Exercice 14 page 176 :
On applique la loi aux noeuds :
* I+115 = 192 d'où I=192-115= 77 mA
* I + 78 +172 =342 d'où I= 92 mA
Exercice 22 page 177:
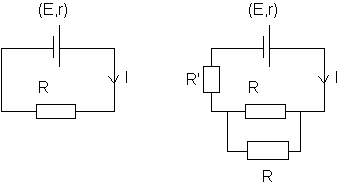
Pour le deuxième circuit , l'association en parallèle des deux résistances est équivalente à une résistance unique R0 = R/2 . Le courant I est le même dans les deux circuits si R'+R0=R ou R'+R/2=R d'où R' =R/2 =3,75 W.
On calcule I en utilisant la loi de Pouillet : E=(R+r)I d'où I=4,55/(7,5+3,75)=0,40 A
Ce courant se divise en deux dans les deux résistances R branchées en parallèle , autrement dit , chacune de ses résistances est traversée par un courant de 0,2 A , circulant de droite à gauche sur le schéma .
Exercice 27 page 177 :
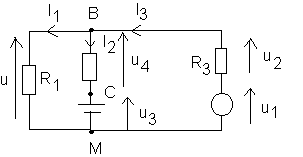
* u= VB - VM . Comme VM=0 (définition de la masse) u= VB .
u=u1+u2 et u2= -R3*I3 = -4,25 V . D'où VB = 12,1-4,25 = 7,85 V
* Nous avons aussi u=R1*I1 , d'où I1= 7,85/7,5= 1,05 A
*I3=I1+I2 d'où I2 = 1,85 - 1,05= 0,8 A
* u=u3+u4 avec u3 = uCM = VC et u4= (1,70)*I2 = 1,36 V
d'où VC= 7,85-1,36 = 6,5 V
Exercice 30 page 178 :
1)
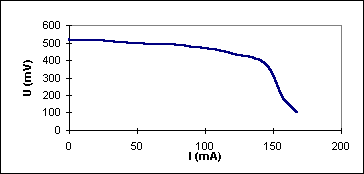
2)
| I(mA) | 0 |
15 |
25,4 |
42,7 |
67 |
82,1 |
111 |
| U (mV) | 518 |
516 |
514 |
506 |
494 |
485 |
458 |
| Peg en 10-6 W | 0 |
7740 |
13056 |
21606 |
33098 |
39819 |
50838 |
123 |
141 |
150 |
156 |
168 |
438 |
400 |
325 |
202 |
100 |
53874 |
56400 |
48750 |
31512 |
16800 |
Il est clair que la puissance Peg = 0,0564 W est maximale pour U= 400 mV et I= 141 mA
3) -a:Les cellules sont branchées en série :La puissance est toujours masimale pour I= 141 mA
b: UPN = 10 * 400 = 4000 mV = 4 V
UPN = R I d'où R = 4/0,141 = 28,4 W .
La puissance dissipée par effet Joule est alors : PJ = RI2 = 28,4 * 0,1412 = 0,56 W
Exercice 44 page 180 :
1/-a : U=RI . Soit R0 = U0/I0 = 4/1,5 = 2,6 W .
Si R> R0 alors I=U/R < I0 et da,s ce cas , d'après la caractéristique U=U0 .
b: Si R< R0 , alors U < U0 : nous somme dans la partie de la caractéristique d'équation I=I0 , ce qui veut dire que l'intensité dans le circuit est égale à I0 .
2/R= 5W > R0 : nous sommes dans le cas a) avec U=U0 et donc I=U0/R =4/5 = 0,8 A . Le point correspondant se situe donc approximativement au milieu de la partie de la caractéristique d'équation U=U0 (point A1 sur le schéma ci-dessous).
3/R=2 W < R0 : nous sommes dans le cas b) . UPN= 2*I0 = 3 V (point A2).
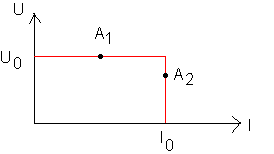
4/ * R>R0 : Per = U0I =U02 / R
* R< R0 : Per = UI0= RI02
