Physique –2de – Exercices de révision

Exercice 1:

En utilisant la notation scientifique, exprimer en mètres les longueurs suivantes:

L₁=150 millions de kilomètres ; L₂=6400 km ;L₃=0,400μm

Exercice 2:

Pour mesurer le diamètre D du bouchon d'une bouteille d'eau minérale on utilise successivement différents instruments.

Un double décimètre: D=3,8cm.
Un pied à coulisse: D=3,82cm

a) Quel est le nombre de chiffres significatifs dans chaque cas?
b) Calculer la surface S du bouchon avec un nombre de chiffres significatifs convenable. On donne l'expression littérale permettant de calculer la surface S d'un cercle de diamètre D:

Exercice 3.

On cherche à déterminer le diamètre D de la Lune. Pour cela on découpe un disque de carton de diamètre d=6,1mm qui, tenu à bout de bras (L=0,70m), occulte (cache) juste le disque lunaire.

a. Faire un schéma simplifié de la situation.

b. Déterminer le diamètre apparent α de la Lune.

c. La distance Terre-Lune, déterminée par la méthode de l'écho laser est TL=3,84.10⁵km. Exprimer littéralement puis calculer le diamètre D de la Lune.

Exercice 4.

a. Déterminer la valeur, en kilomètre, d'une année de lumière (a.l). Vous donnerez le résultat avec un nombre de chiffres significatifs convenable.

b. Donner l'ordre de grandeur correspondant à la valeur trouvée précédemment.

Exercice 5.

L'un des rayons d'un faisceau de lumière se propageant dans l'air pénètre dans un diamant d'indice de réfraction 2,43.

a. Schématiser la situation.

b. Écrire la seconde loi de Descartes.

c. Calculer l'angle d'incidence permettant d'obtenir un angle de réfraction de 20°.

Exercice 6.

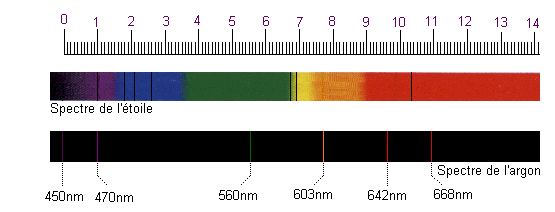
On a obtenu le spectre d'une étoile avec un spectrographe à réseau. Les distances séparant deux raies sont proportionnelles à la différence des longueurs d'onde correspondantes.
On fournit aussi le spectre d'émission de l'argon. Les longueurs d'onde correspondant aux raies de cet élément sont indiquées en dessous.

1. Quel est l'intérêt de fournir le spectre de l'argon?

2 .Expliquer la différence de nature entre les spectres représentés.

3. Déterminer les longueurs d'onde des raies présentes dans le spectre de l'étoile.

Exercice 7.

Une gomme de masse m=10,0g est posée sur une table inclinée.

1. Schématiser la situation.

2. Rappeler la relation existant entre la valeur du poids et la masse du corps (en précisant les unités des grandeurs figurant dans cette relation).

3 Calculer la valeur du poids de la gomme.

4. Représenter le poids à l'échelle 10cm <-> 0,1N.

5. Cette représentation est-elle valable si la gomme glisse?

Donnée: g = 9,81N.kg^-1.

Exercice 8

On reprend l'exercice précédent

1.On suppose que le contact entre la gomme et la table est sans frottement . Sur un schéma , représenter les forces appliquées à la gomme.

2.Que peut-on dire de la somme vectorielle des forces appliquées à la gomme : est-elle nulle ?

3.Nous supposons à présent que la gomme est au repos (immobile). Ecrire la condition d'équilibre de la gomme et représenter dans ce cas sur un schéma les forces appliquées à la gomme .

Exercice 9 :

Trois fils de masse négligeable sont accrochés à un anneau A de masse négligeable . A est maintenu en équilibre comme l'indique le schéma ci-dessous : un corps B de masse m est directement fixé à A, tandis qu'un autre corps C, de masse M est fixé à A par l'intermédiaire d'une poulie P.

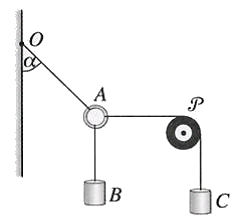
1.Faire le bilan des forces qui s'exercent sur A.

2.Représenter les forces appliquées à l'anneau dans un repère Oxy en plaçant l'origine de ces forces en O .

3.Ecrire la condition nécessaire vectorielle d'équilibre de l'anneau.

4.En déduire les relations entre les coordonnées de ces forces dans le repère Oxy (théorème des projections).

5.Exprimer ces coordonnées en fonction des normes des différentes forces et de l'angle α.

6.On admet que le fil auquel est suspendu le solide C exerce sur l'anneau une force dont l'intensité est égale à M*g (g=10 N.kg^-1) . L'angle α est égal à 45°; La masse de B est égale à m = 0,4 kg.; La masse de B est égale à m = 0,4 kg. Déterminer la masse de M de C.

Exercice 10.

Deux enfants A et B s'amusent sur un manège. Ils sont assis sur des chevaux de bois diamétralement opposés. Le manège tourne. Préciser pour chaque question le référentiel d'étude.

1. Quel est le mouvement de A par rapport à B?

2. Quel est le mouvement de A par rapport au manège?

3. Quel est le mouvement de A par rapport à un spectateur immobile par rapport au sol?

Exercice 9.bis

On considère un satellite qui tourne autour de la Terre sur une orbite circulaire à une altitude de 400km. Il effectue un tour de la Terre en 1h33min.

1. En utilisant le principe de l'inertie, montrer que le satellite est soumis à une force. Qui exerce cette force sur le satellite? Faire un schéma et représenter cette force.

2. Quel est le meilleur référentiel pour étudier le mouvement du satellite? Déterminer la vitesse du satellite dans ce référentiel.

Exercice 10.bis

Depuis un point O situé sur la Terre, on lance avec une vitesse V un solide de petite dimension dans une direction faisant un angle α avec l'horizontale. La vitesse de lancement (vitesse initiale) est suffisamment faible pour que l'on puisse considérer les frottements de l'air comme négligeables. La position du mobile est repérée à intervalles de temps réguliers (voir enregistrement ci-contre).

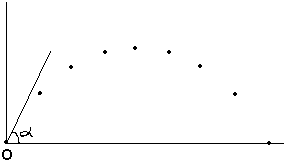
1. En utilisant le principe de l'inertie, montrer que le solide n'est ni isolé ni pseudo-isolé.

2. En un point quelconque de la trajectoire, représenter la force qui agit sur le solide. Nommer cette force.

3. On projette les positions successives du mobile sur un axe perpendiculaire à la force évoquée à la question Quelle est la particularité du mouvement de la projection du solide.

4. Quelle conclusion relative au mouvement d'un corps soumis à une force de direction constante vous inspire le résultat de l'étude faite à la question 3?

Exercice 11 : Vrai ou faux

1- 2-

3 - Un objet est lancé verticalement vers le haut. La vitesse de son centre d'inertie s'annule à l'instant où il atteint son altitude maximale avant de retomber. L'objet est pseudo-isolé à cet instant.

4 - La somme des forces extérieures qui s'exercent sur une automobile qui se déplace à vitesse constante sur une route rectiligne est nulle.

Exercice 12 :

La terre a une masse de 5,98.10²¹ tonnes, la lune a une masse égale à 1/83 de la masse de la terre. La distance terre-lune varie entre 356675 km et 406720 km.

1/donner l'expression des forces d'interaction gravitationnelle entre les deux planètes.

2/Calculer la valeur de cette force entre la terre et la lune lorsque la distance entre les deux planètes est :

a-la plus petite

b-la plus grande.

Exercice 13 :

On visualise sur l'écran d'un oscillographe une tension en dents de scie . L'écran est représenté ci-dessous :

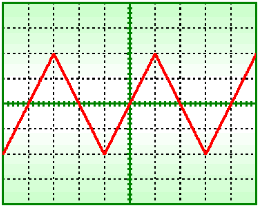
Les réglages sont les suivants :

- sensiblité de la base de temps : 5 ms.div^-1

-sensibilit& verticale : 1 V.div^-1

a)Quelle est la période T de la tension observée ?

b)En déduire la valeur de la fréquence.

c)Quelle est la valeur :

c-1 : de la tension crête à crête ?

c-2 : de l'amplitude ?

Physique –2de – Exercices de révision - CORRECTION

Exercice 1:

L₁= 150.10⁶ km = 150.10⁶*(10³ m) = 150.10⁹ m (car 1 km=10³ m)

L₂ = 6400.10³ m = 6,4.10⁶ m

L₃= 0,400* (10^-6 m) = 4.10^-7 m ( car 1 μm = 10^-6 m)

Exercice 2:

a)On mesure avec un double décimètre: D=3,8cm : 2 chiffres significatifs
On mesure avec un pied à coulisse: D=3,82cm : 3 chiffres significatifs

b) Si on fait la mesure avec le double-décimètre : S = π*D²/4= π*(3,8)²/4= 11 cm² (résultat avec 2 chiffres significatifs)

Si on mesure avec le pied à coulisse S= π*3,82²/4 =11,5 cm² (résultat avec 3 chiffres significatifs)

Exercice 3.

a. Schéma simplifié de la situation.

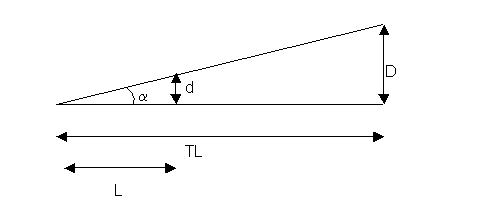
TL est la distance terre-lune , L la longueur du bras , d le diamètre du disque , D le diamètre de la lune et α le diamètre apparent de la lune .

b.tg α = d/L = 6,1 mm/700 mm = 8,7.10^-3 . α est le diamètre apparent de la lune α = tang^-1(8,7.10^-3)= 0,5 °

c. Nous avons aussi tg α = D/TL d'où D=tg α;*TL = 8,7.10^-3*3,84.10⁵ km = 3340 km

Exercice 4.

a. La célérité (ou vitesse) de la lumière dans le vide est c=3.10⁸ m.s^-1 . Une année lumière (a.l.) est égale à la distance parcourue par la lumière en un an : L=c* (365,25*24*3600) = 3.10⁸ m.s^-1 * 3,15.10⁷ s = 9,46.10¹⁵ m = 9,46.10¹² km (résultat donné avec 3 chiffres significatifs)

b. L'ordre de grandeur est de 10¹³ km..

Exercice 5.

a. Schéma de la situation.

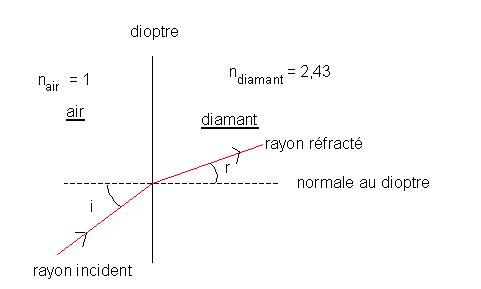
b. La seconde loi de Descartes s'écrit n_air sin i = n_diamant sin r

c.De la seconde loi de Descartes nous déduisons :

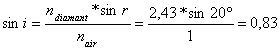
. Et par conséquent : i = sin^-1 0,83= 56,2 °.C'est l'angle d'incidence qui permet d'obtenir un angle de réfraction de 20°.

Exercice 6.

1. Le spectre de l'argon permet d'étalonner le spectrographe , c'est à dire qu'en déterminant la position d'une raie en "divisions" , nous pouvons en déduire la longueur d'onde correspondante .

2 Le spectre de l'argon est un spectre d'émission (raies de couleur sur fond noir) alors que le spectre de l'étoile est un spectre d'absorption (raies noires sur fond de spectre de la lumière blanche)

3. Le tableau ci-dessous donne la correspondance entre les longueurs d'onde des raies du spectre de l'argon et les divisions du spectrographe .

Nous pouvons alors tracer la courbe λ = f(d) :

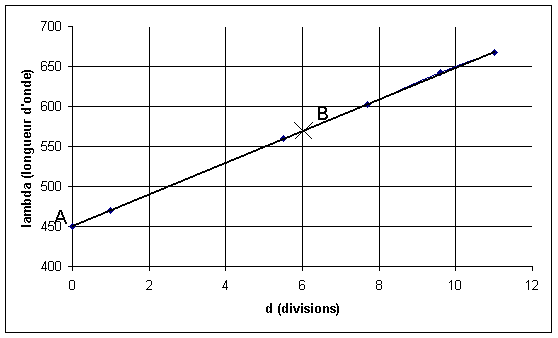
La courbe est donc une fonction affine. Déterminons l'équation de cette courbe . A a pour coordonnées (d_A=0 div ; λ_A=450 nm) . B a pour coordonnées (d_B= 6 div ; λ_B= 570 nm) . Le coefficient directeur de cette courbe est donc :

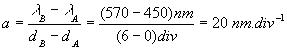
Il est clair que l'ordonnée à l'origine de cette droite est b= 450 nm

L'équation de la droite est par conséquent λ= 20*d + 450 ( d en div et λ en nm)

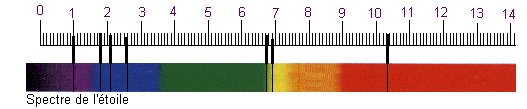
Reprenons le spectre de l'étoile et établissons la correspondance entre les différentes raies et les divisions du spectrographe (les raies sont numérotées de gauche à droite de 1 à 7) :

En utilisant la fonction λ=f(d) précédemment trouvée , à partir de chaque valeur de d , nous pouvons en déduire par le calcul la longueur d'onde correspondante . Les résultats obtenus sont rassemblés dans le tableau ci-dessous :

Remarque : il est aussi possible de faire une lecture directe sur la courbe λ=f(d) pour déterminer les longueurs d'onde des raies absorbées.

Exercice 7.

1. Schématiser la situation.

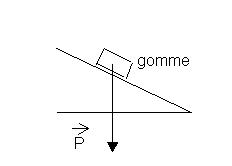
2. P=mg : c'est la relation demandée .P s'exprime en Newton (N) , m en kg et g en N.kg^-1 .

3. P = 10.10^-3 * 9,81=0,098 N = 9,8.10^-2 N

4. L'échelle proposée est équivalente à 100 cm <---> 1 N. Le poids sera représenté par une flèche verticale (orientée vers le bas) de 9,8.10^-2*100= 9,8 cm (le vecteur poids représenté , pour des raisons de place ne correspond pas à cette échelle)

5. La représentation du poids est la même que la gomme soit en mouvement ou au repos .

Exercice 8

1.

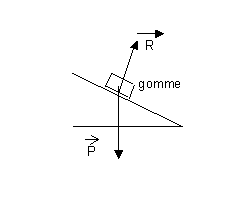
est l'action de la table sur la gomme (sans frottement) , est l'action de la terre sur la gomme .

2.La somme vectorielle des forces appliquées à la gomme n'est pas nulle (la gomme ne peut pas être immobile)

3.La condition nécessaire d'équilibre de la gomme s'écrit ce qui nous amène au bilan de forces ci-dessous :

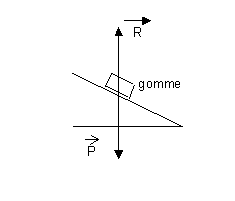
Il est clair que pour que la gomme soit en équilibre (ou au repos) il faut qu'il y ait un frottement entre la gomme et la table ( n'est pas perpendiculaire aux surfaces en contact)

Exercice 9 :

1.Bilan des forces qui s'exercent sur A.

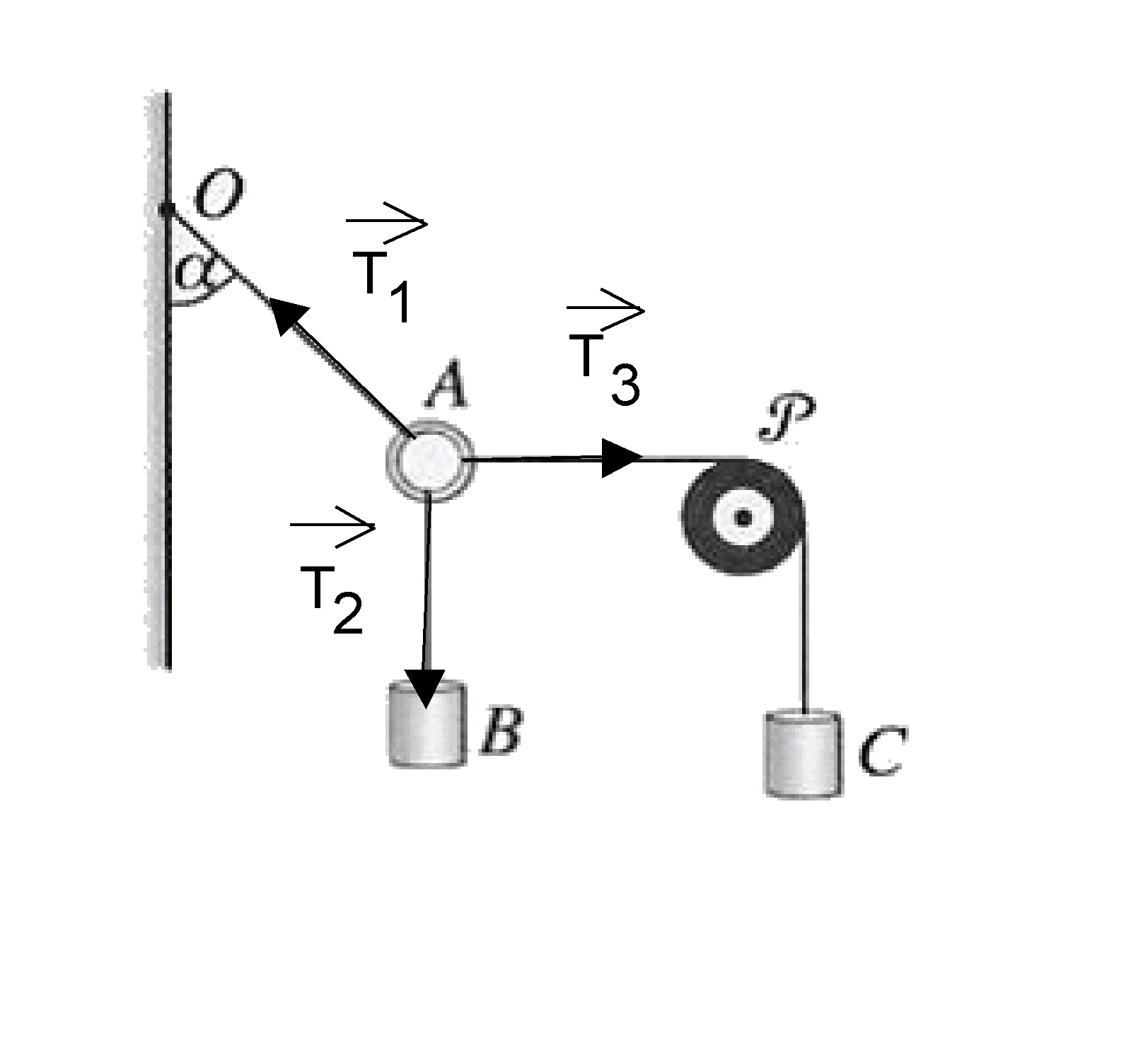
est l'action du fil OA sur l'anneau

est l'action du fil AB sur l'anneau

est l'action du fil AC sur l'anneau

Montrons que T₂=P_B (poids du solide B) . Pour cela faisons le bilan des forces appliquées au solide B :

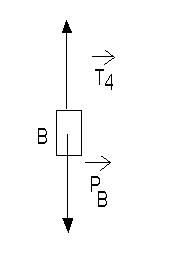
Comme le solide B de masse m_B est en équilibre , nécessairement , la somme vectorielle des forces appliquées à ce solide est nulle :

Cette égalité vectorielle implique que P_B=T₄ . Or est l'action du fil AB sur la masse m_B. Nous retiendrons qu'un fil de masse négligeable (ce qui est le cas ici) "transmet" les tensions , ce qui signifie ici que T₄=T₂ et par conséquent T₂=P_B=m_B*g

2.Rapportons les forces appliquées à l'anneau à l'origine O d'un repère Oxy :

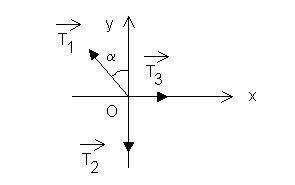
L'angle α est reporté sur le schéma comme angle alterne-interne

3.Comme l'anneau est en équilibre , alors nécessairement :

4.Le théorème des projections s'écrit ici :

*en projetant sur Ox : T_1,x+T_2,x+T_3,x =0

*en projetant sur Oy : T_1,y+T_2,y+T_3,y=0

5.Les mesures algébriques sont telles que :

T_1,x= -T₁sin α ; T_2,x=0 ; T_3,x=T₃ ; T_1,y=T₁cos α ; T_2,y= - T₂ ; T_3,y = 0 et donc :

- T₁sin α + T₃ =0 (1)

T₁cos α - T₂=0 (2)

6.Nous savons que par ailleurs (énoncé) : T₃= Mg et nous avons démontré que T₂=m_B*g =m*g (sachant que m= m_B).

De l'équation (1) ci-dessus nous déduisons T₁ = T₃/(sin α) . En reportant T₁ dans l'équation (2) , nous obtenons :

Ce qui donne finalement :

Exercice 10.

1. Mouvement de A par rapport à B: le référentiel d'étude est B

2. Mouvement de A par rapport au manège : le référentiel d'étude est le manège

3. Mouvement de A par rapport à un spectateur immobile par rapport au sol: le référentiel d'étude est le sol (ou le spectateur)

Exercice 9.bis

1. Si le satellite n'était soumis à aucune force , dans la mesure où il est en mouvement il aurait un mouvement rectiligne uniforme d'après le principe d'inertie , ce qui signifie notamment que sa trajectoire serait une droite . Or ici , sa trajectoire est un cercle : l'hypothèse qui consisterait à dire que le satellite ne serait soumis à aucune force est donc mauvaise . Le solide est par conséquent soumis à une force .

C'est la terre qui exerce cette force sur le solide : il s'agit de la force gravitationnelle . Celle-ci est représentée sur le schéma ci-dessous :

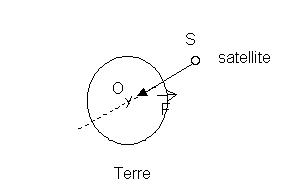
Cette force passe par le centre de la terre est sa valeur se calcule à partir de la formule :

G est la constante gravitationnelle (G=6,67.10^-11 SI) , M_T la masse de la terre et m_S la masse du satellite .

2. Le meilleur repère-référentiel d'étude pour le mouvement de ce satellite est le référentiel géocentrique : il s'agit d'un repère-référentiel dont l'origine est au centre de la terre et les axes dirigés vers trois étoiles fixes .

Si l'altitude du satellite est de 400 km , comme le rayon de la terre est égal à R_T = 6370 km , alors OS=6370+400= 6770 km . Le satellite décrit par conséquent un cercle de rayon OS= 6770 km . Le périmètre de ce cercle est L =2*π*OS =42530 km =42530 * 10³ m. La durée que met le satellite pour faire un tour est : Δt=1h 33 mn=60+33= 93 mn = 93*60 = 5580 s.

La vitesse se calcule à partir de la formule

Comme 1 m.s^-1 = 10^-3 km*(1/3600)^-1 =3600*10^-3 km.h^-1 = 3,6 km.h^-1 , nous en déduisons :

v= 7620 * 3,6= 27430 km.h^-1 .

Exercice 10. bis

1. Si le solide était isolé ou pseudo-isolé , d'après le principe d'inertie , dans la mesure où le solide est en mouvement , ce mouvement serait rectiligne et uniforme . Or ce n'est pas le cas puisque la trajectoire n'est pas rectiligne . Le solide n'est par conséquent ni isolé , ni pseudo-isolé .

2. La seule force appliquée au solide est une action à distance : il s'agit de l'action de la terre sur la masse du solide .Cette force n'est autre que le poids du solide (celui-ci est égal à la force gravitationnelle entre le solide et la terre)

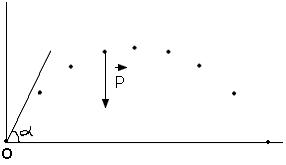
3.

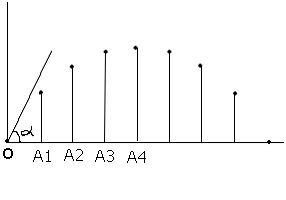
Les positions successives du mobile sur un axe perpendiculaire à la force évoquée à la question précédente sont telles que OA₁=A₁A₂=A₂A₃=A₃A₄ ............... Cela signifie que les distances entre deux pointages successifs du mouvement projeté du solide sont égales . Or ces pointages ont lieu à intervalles de temps successifs égaux . Autrement dit le mouvement projeté du solide (dans la direction de la force appliquée) est tel que la distance parcourue pendant des intervalles de temps identiques est toujours la même .Cette propriété est caractéristique d'un mouvement à vitesse constante , c'est à dire uniforme : Le mouvement projeté du solide est rectiligne uniforme.

4. Nous en déduisons :dans le référentiel terrestre, lorsqu'un corps se déplace en étant soumis à une force de direction constante (ici sont poids), sa vitesse dans la direction perpendiculaire à celle de la force est constante n'est pas modifiée.

Exercice 11 : Vrai ou faux

1- : Faux 2- : vrai

3 - Un objet est lancé verticalement vers le haut. La vitesse de son centre d'inertie s'annule à l'instant où il atteint son altitude maximale avant de retomber. L'objet est pseudo-isolé à cet instant. : faux (quel que soit sa position , l'objet est toujours soumis à son poids)

4 - La somme des forces extérieures qui s'exercent sur une automobile qui se déplace à vitesse constante sur une route rectiligne est nulle : Vrai (affirmation équivalente à la 2-)

Exercice 12 :

1/Appelons TL la distance entre le centre de la lune et le centre de la terre . M_T= 5,98.10²⁴ kg est la masse de la terre ; M_L= 5,98.10²⁴ /83=7,20.10²² kg est la masse de la lune. G=6,67.10^-11 m³.kg^-1.s^-2 est la constante gravitationnelle . L'expression de la force d'interaction gravitationnelle entre les deux planètes est

2/Calculer la valeur de cette force entre la terre et la lune lorsque la distance entre les deux planètes est :

a-lorsque TL₁=356675 km :

b-lorsque .TL₂=406720 km :

Exercice 13 :

Les réglages sont les suivants :

- sensiblité de la base de temps : 5 ms.div^-1

-sensibilité verticale : 1 V.div^-1

a)La période du signal mesurée en divisions sur l'écran est X_T = 4 divisions . Comme la sensibilité de la base de temps est β= 5 ms.div^-1 , nous en déduisons T=β*X_T = 5*4 = 20 ms

b)Nous en déduisons la fréquence f :.

f=1/T = 1/20.10^-3 = 50 Hz (attention à l'unité de la période !)

c-1 :tension crête à crête : V_CC = α*Y_CC =1 *4 V.div^-1.div = 4 V .

Y_CC est la tension crête à crête mesurée en divisions sur l'écran de l'oscillographe : Y_CC = 4 div . α est la sensibilité verticale de la voie utilisée α =1 V.div^-1

c-2 :l'amplitude est V_m=V_CC/2 = 2 V